Аффинные преобразования

Определение 1: аффинным преобразованием аффинного пространства 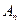называется его изоморфное отображение на себя.

Замечание 1: изоморфное отображение векторного пространства 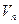на себя является его линейным преобразованием. Поэтому можно также называть аффинным преобразованием такое преобразование пространства 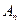, для которого в связанном с 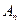векторном пространстве 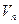существует ассоциированное линейное преобразование.

Замечание 2: так как преобразование, ассоциированное с аффинным, является линейным, то оно сохраняет линейную независимость векторов: линейно независимая система векторов отображается также на линейно независимую систему векторов с сохранением коэффициентов. Например, если

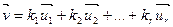
и векторы 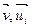отображаются соответственно на векторы 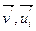, то

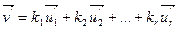
Поэтому любой базис векторного пространства 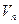, связанного с 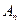, отображается также на некоторый базис этого пространства 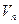, а подпространство 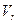пространства 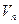отображается на некоторое подпространство 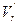той же размерности.

Теорема 1: при аффинном преобразовании пространства 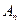любая плоскость отображается на плоскость той же размерности, причем сохраняется параллельность плоскостей.

□ 1) Плоскость 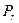, натянутая на точку 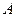и подпространство 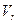, есть множество точек, получаемых при откладывании от точки 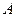всех векторов из 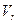. Аффинное преобразование отображает точку 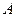на некоторую точку 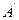, а ассоциированное с ним векторное преобразование отображает 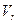на некоторое подпространство 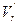, следовательно, плоскость 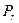отображается на некоторую плоскость 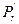, натянутую на 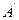и .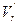

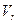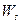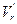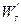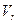
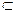
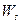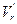
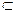
2) Если ассоциированное с аффинным векторное преобразование отображает подпространства и соответственно на и , причем , то имеем 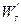, то есть из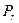 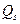следует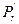 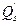- параллельность плоскостей сохраняется. ■

Теорема 2: при аффинном преобразовании пространства 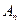всякая аффинная система координат 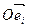отображается также на некоторую аффинную систему координат 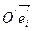, а любая точка 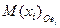отображается на точку 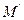с такими же координатами в системе .

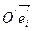□ 1) Пусть данное аффинное преобразование отображает начало координат 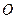на некоторую точку 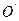, а ассоциированное с ним векторное преобразование отображает векторы базиса 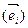на некоторые векторы 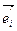. Так как векторы 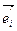также образуют некоторый базис пространства 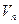, то имеем аффинную систему координат 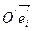и первая часть теоремы доказана.

2) По определению координат точки имеем: 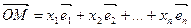, но векторное преобразование, ассоциированное с данным аффинным, не изменяет коэффициентов 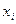, поэтому .

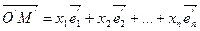Таким образом 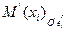, то есть числа 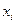являются координатами точки 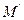в системе . ■

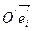Замечание 3: определить аффинное преобразование можно и по-другому, например: аффинным называется преобразование, отображающее 1) любую прямую также на прямую и 2) сохраняющее простое отношение точек, то есть число 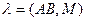такое, что 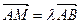. При этом можно доказать эквивалентность двух определений аффинного преобразования. Требование (2) может быть доказано как теорема.

Дата добавления: 2014-01-07