
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Модульная единица 3 Проверка гипотез относительно доли признака. Проверка гипотезы о принадлежности резко выделяющихся значений признака исследуемой совокупности
|
|
|
|
Резюме
Вопросы для повторения
14-1 В чем разница между выборками зависимыми и независимыми?
14-2 Как формулируется нулевая гипотеза о средних при независимых выборках?
14-3 Какие четыре ситуации возможны при проверке гипотезы относительно двух средних при независимых выборках?
14-4 При каких ситуациях необходим расчет усредненной дисперсии?
14-5 В чем особенность расчета числа степеней свободы при неравных дисперсиях?
14-6 Что такое НСР?
14-7 Как формулируется нулевая гипотеза при зависимых выборках?
14-8 Каков алгоритм расчета фактического значения критерия при зависимых выборках?
Проверка гипотезы относительно средних требует предварительного уяснения каков характер выборки (зависимые или независимые), и если выборки независимые к какой из 4-х ситуаций принадлежат выборочные данные. В зависимости от этого меняется алгоритм расчета фактического значения критерия и поиск его табличного значения
Цель изучения модульной единицы
Перед рассмотрением последующего материала сразу следует сделать оговорку, что речь идет о доле качественного альтернативного признка
Если речь идет о предположении, что в генеральной совокупности доля альтернативного признака равна некоторой величине Q, то последовательность проверки такой гипотезы будет следующей:
Выдвигаются две гипотезы Н9: Р=Q и альтернативная Р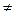 Q
Q
В качестве критерия для проверки гипотезы относительно доли признака используется критерий t - нормального распределения, фактическое значение которого определяется по формуле  , где p – доля единиц определенного качества по выборке, g - доля единиц противоположного качества по выборке; n – численность выборки.
, где p – доля единиц определенного качества по выборке, g - доля единиц противоположного качества по выборке; n – численность выборки.
Полученное фактическое значение сравнивается с табличным, которое зависит только от уровня значимости и делается соответствующий вывод.
Если речь идет об оценке различий в долях по двум выборкам, то последовательность проверки гипотезы будет следующей:
Выдвигается нулевая гипотеза о равенстве долей в двух генеральных совокупностях,  то есть
то есть  :
:  . В качестве альтернативной гипотезы может быть выдвинута ненаправленная
. В качестве альтернативной гипотезы может быть выдвинута ненаправленная 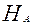 :
:  или направленная гипотеза
или направленная гипотеза 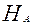 :
:  (
(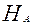 :
: 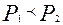 ).
).
В качестве критерия для проверки выдвинутых гипотез используется критерий t - нормального распределения, который рассчитывается по двум алгоритмам: если каждая из выборочных доли ( ) лежит в интервале
) лежит в интервале 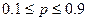 , то формула для расчета фактического значения критерия будет следующей
, то формула для расчета фактического значения критерия будет следующей 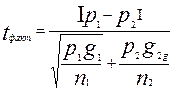 , где
, где 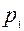 - доля единиц с определенным качеством по первой выборке;
- доля единиц с определенным качеством по первой выборке;  - доля таких единиц по второй выборке;
- доля таких единиц по второй выборке; 
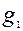 ,
,  - доля единиц с противоположным качест
- доля единиц с противоположным качест
вом соответственно по первой и второй выборкам; 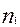
 и
и 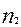 численности выборок.
численности выборок.
Если же хотя бы одна из выборочных долей лежит вне указанного выше интервала, то для расчета фактического значения критерия требуется предварительное 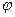 (фи) преобразование выборочных долей, при этом значения
(фи) преобразование выборочных долей, при этом значения  находятся по специальным таблицам. Фактическое значение критерия t –нормального распределения находят по формуле:
находятся по специальным таблицам. Фактическое значение критерия t –нормального распределения находят по формуле:
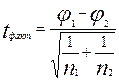 , где
, где  и
и  - преобразованные значения выборочных долей
- преобразованные значения выборочных долей
При проверке гипотезы относительно принадлежности резко выделяющихся значений исследуемой совокупности в качестве нулевой гипотезы выдвигается предположение, что резко выделяющееся значение признака принадлежит исследуемой совокупности.
При выборе критерия возможно два варианта в зависимости от численности выборки. Если она меньше 25 единиц, то в качестве критерия следует использовать критерий Диксона. Фактическое значение данного критерия определяется по формуле: М =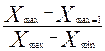 (для случая, когда резко выделяется максимальное значение признака). В этой формуле
(для случая, когда резко выделяется максимальное значение признака). В этой формуле 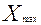 - максимальное значение признака относительно которого выдвигается гипотеза;
- максимальное значение признака относительно которого выдвигается гипотеза;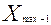 - значение признака предшествующее в ранжированном ряду максимальному;
- значение признака предшествующее в ранжированном ряду максимальному;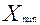 - минимальное в ранжированном ряду значение признака.
- минимальное в ранжированном ряду значение признака.
Для случая, когда сомнение о принадлежности вызывает минимальное значение признака, фактическое значение критерия Диксона определяется по формуле М = , где
, где 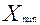 - минимальное значение признака относительно которого выдвигается гипотеза;
- минимальное значение признака относительно которого выдвигается гипотеза; - следующее за минимальным в ранжированном ряду значение признака;
- следующее за минимальным в ранжированном ряду значение признака; 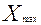 - максимальное значение признака.
- максимальное значение признака.
Если численность выборки превышает 25 единиц, то в качестве критерия проверки гипотезы о принадлежности единицы исследуемой совокупности используется критерий t –нормального распределения, фактическое значение которого определяется по формуле 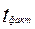 =
=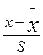 , где
, где  - значение признака относительно которого выдвинута гипотеза;
- значение признака относительно которого выдвинута гипотеза; 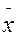 - среднее значение признака по исследуемой выборочной совокупности;
- среднее значение признака по исследуемой выборочной совокупности;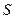 - среднее квадратическое отклонение признака по исследуемой выборочной совокупности
- среднее квадратическое отклонение признака по исследуемой выборочной совокупности
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 614; Нарушение авторских прав?; Мы поможем в написании вашей работы!