Физический смысл степени превращения: теоретический выход продукта реакции по данному исходному веществу

Использование мольных единиц измерения количества ве­ществ позволяет просто описывать реакции, происходящие между ними - с помощью закона стехиометрических соотношений. Практическим его выражением являются стехиометрические уравнения.

Стехиометрическое уравнение - соотношение, ycтанавливающее мольные пропорции, в которых реагиру­ют химические вещества с образованием продукта реак­ции.

Стехиометрические коэффициенты - коэффициенты, стоящие перед химической формулой данного химического вещества в стехиометрическом уравнении и показывающие его количество в молях.

Например, для реакции полимеризации мономера М, иниции­рованной инициатором I с образованием полимера, содержаще­го n звеньев мономера в одной макромолекуле, стехиометричес­кое уравнение имеет вид:

nМ + mI = M_n I_m,

а для поликонденсации эквимолярной смеси двух бифункцио­нальных мономеров М₁ и М₂, протекающей с выделением низ­комолекуляронгo продукта L:

nМ₁ + nМ₂ = (М₁ M ₂)n + (n-l)L.

В случае сложных реакционных систем, с участием многих веществ, система стехиометрических уравнений может быть очень большой, не имеющим простого решения. Для упрощения выделяют ключевые уравнения.

Для характеристики количественного состава реакционной смеси необходимо знать количества ключевых веществ. Ключевы­ми являются вещества, количества которых однозначно определя­ют состав реакционной системы.

Балансовые соотношения при полимеризации

Уравнение материального баланса - уравнение, устанавливающее взаимо­связь между начальным и конечным (после реакции) составом реакционной смеси. Уравнения материального баланса по конкретным веществам устанавливают взаимосвязь для каж­дого из них с учетом степени их превращения в ходе реакции.

Наиболее общая схема процессов цепной полимеризации может быть представлена в виде последовательности стадий, состоящих из элементарных реакций:

• стадия зарождения цепи, включающая в себя разложение молекулы инициатора I и образование ре­акционного центра реакцией осколка инициатора с молекулой мономера IM.

• стадия роста цепи IMMM

• стадия обрыва цепи рекомбинацией и/или диспропорциони­рованием активных макромолекул

IM_p + IM_q

Стехиометрия реакции полимеризации реакции полимеризации:

nМ + mI = M_n I_m, где n, m - стехиометрические коэффициенты определяемые как:

m= (R+1)/ s, где

s - число активных частиц, образующихся при распаде иници­ирующего вещества,

R - изменение числа молей в реакции обрыва цепи.

Обычно в инициируемой инициаторами радикальной цеп­ной полимеризации s = 2, но в ряде случаев s = 1. Это, напри­мер, имеет место при инициировании смесями пероксидов с солями металлов пере мен ной валентности или с третичными аминами.

R принимает значения 0 (нуль) в случае обрыва цепи по реакции диспропорционирования и 1 - в случае рекомби­нации.

Таким образом, реакция полимеризации оказывается стехио­метрически простой, и для ее описания достаточно знать коли­чество (концентрацию) одного ключевого вещества, в качестве которого обычно принимается мономер.

Наиболее распространенная радикальная цепная полимериза­ция инициируется инициаторами, которые при термическом распаде дают два активных осколка, т.е. S = 2.

Под n подразумевается среднечисловая степень полимеризации P, которая легко определяется из мольных материальных балансов по исходному веществе (мономеру) и инициатору:

Р= (N_om - N_m)/ (N_I0 - N_I) * κ, где

N_0m и N_0I количество мономера и инициатора (в молях) в начальный момент времени

N_m и N_I количество мономера и инициатора (в молях) в текущий момент времени t. соответственно.

κ – коэффициент, зависящий от доли обрыва цепи (λ) = от 0 до 1, и числа активных частиц, образующихся при распаде иници­ирующего вещества (s), и определяемый как:

κ = (1+λ)/s

Физический смысл полученного уравнения очевиден: содержание молекул мономера в одной молекуле полимера есть молярное отношение количества превращенного мономера к количеству превращенного инициа­тора, т.е. к количеству активных центров, на которых протекал процесс полимеризации. Множитель перед этим отношением представляет собой поправку на число активных центров, обра­зующихся при распаде одной молекулы инициатора, и характер образования неактивной макромолекулы (рекомбинацией или дис­пропорционированием). Таким образом, значение средней сте­пени полимеризации зависит от типа реакций зарождения и обрыва физической цепи роста макромолекул.

Уравнение является основой для материальных рас­четов процессов полимеризации по заданной степени полимери­зации (средней молекулярной массе полимера), однако в реаль­ных балансах необходимо учитывать чистоту реагентов, степень их превращения и неизбежные технологические потери, а также эф­фективность использования инициатора.

Балансовые соотношения при поликонденсации (полиприсоединении)

Стехиометрические соотношения в поликонденсации более сложны по сравнению с полимеризацией из-за большего коли­чecтва и большого разнообразия мономеров различной функциональности. Основой для их опи­сания является то, что в эквимолярных количествах в общем случае реагируют функциональные группы, а не молекулы мо­номеров. Важным следствием этого является различие понятий концентраций функциональных групп (С_f) и мономеров (М). Отсюда следует важный вывод: совпадение степени превращения разных функциональных групп и степени превращения мономеров имеет место только в том случае, когда функциональности мономеров равны, в ином случае степени пре­вращения не будут совпадать.

Наиболее просто описываются стехиометрические соотноше­ния в процессах поликонденсации соединений, содержащих способные к взаимодействию друг с другом группы в одной и той же молекуле. Это относится, например, к поликонденсации олигомерных полиметиленгликолей

НО(СН₂)_nОН и т.п. Иногда такие процессы называют линейной гомополиконденсацией. Стехиометрическое урав­нение для них очевидно:

n(НО (СН₂)ОН) = НО (СН₂)_nОН + (n - l) Z,

где р и q - реагирующие функциональные группы, а Z – низкомолекулярный побочный продукт.

Материальный баланс по мономеру имеет вид:

[M]₀=[M] + Σ n[M_n ] + Σ (n-1)Z,

Сложение по n идет от 1 до ∞. Причем последний член в правой части учитывается только в процессах поликонденсации.

Из формулы следует, что в поликонденсации и полипри­соединении концентрация полимера в ходе реакции не изменяется, а растет лишь его средняя степень поликонденсации (присоедине­ния). Мономер здесь рассматривается как полимер со степенью поликонденсации единица.

Действительно, при достаточно больших степенях поликон­денсации суммарной концентрацией олигомеров можно прене­бречь по сравнению с остаточной концентрацией мономера.

Определение средней степени поликонденсации

P = [M]₀ /[M]

Таким образом, степень превращения мономера является единственным параметром, контролирующим как временной ход процесса, так и параметры образующегося продукта.

Молекурярно-массовое распределение (ММР)

К числу наиболее важных характеристик по­лимеров, зависящих от технологии син­теза, относятся:

• величина средней степени полимеризации (средней моле­кулярной массы) и рассеяние (дисперсия) вокруг нее (степень полидисперсности);

• величина (степень) разветвленности;

• степень упорядоченности распределения мономерных зве­ньев в макромолекуле (чередующиеся, статистические, приви­тые, блоксополимеры, смеси (сплавы) гомополимеров и т.п.) ­для продуктов совместной полимеризации нескольких мономе­ров (сополимеров).

Принятой мерой среднего размера макромолекулы является средняя степень полимеризации (Р), показывающая усредненное по всей смеси по определенному признаку число звеньев мономера, со­держащееся в одной молеку­ле полимера. Для полимеров различают среднечисловую, среднемассовую и среднеседиментационную степень полимеризации. Среднемассовая степень полимеризации - степень полимеризации, усредненная по массе макромолекул дан­ного размера. Среднечисловая степень полимеризации - степень по­лимеризации, усредненная по числу макромолекул данной длины. Величина степени полимеризации совпадает с наиболее вероятным средним значением числа звеньев мономера в одной макромолекуле.

Вторым параметром ММР является мера рассеяния значений этой величины вокруг среднего, или ее дисперсия. Наглядно типичные кривые моле­кулярно-массового распределения показаны на Рис.1: унимодальное нормально логариф­мическое (сплошная кривая), уни­модальное наиболее вероятное би­номиальное (пунктирная), бимо­дальное (штриховая).

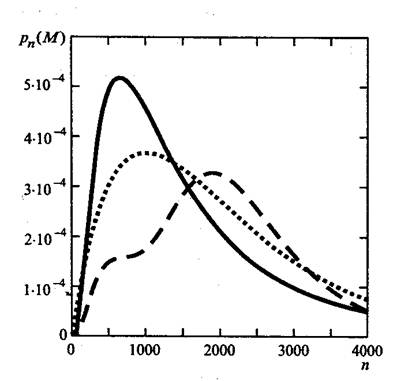
Рис. 1. Унимодальное нормально логариф­мическое (сплошная кривая), уни­модальное наиболее вероятное би­номиальное (пунктирная), бимо­дальное (штриховая) ММР.

В технологии линейных полимеров степень ветвления чаще оценивается числом ветвлений на 1000 атомов углерода ос­новной цепи. Например, в ПЭВД на каждые 1000 атомов ос­новной цепи приходится 30-50 ответвлений в виде от этиль­ных до гексильных групп, в ПЭНД их меньше 8, а в ПЭСД­ меньше 5.

Получение оценок значений средних молекулярных масс по­лимеров производится экспериментально путем измерения свойств их растворов в растворителях. Свойства растворов, про­порциональные числу растворенных молекул, такие, как пони­жение температуры замерзания раствора полимера (метод кри­оскопии), повышение температуры его кипения (метод эбули­оскопии), изменение осмотического давления (метод осмометрии) - дают возможность оценки среднечисловых мо­лекулярных масс. Свойства растворов, зависящие от массы (объе­ма) макромолекул, такие как рассеяние света, диффузионные и др., позволяют оценить значения среднемассовых молекулярных масс.

Широко распространенные (вследствие простоты определения) средневязкостные моле­кулярные массы M_η, которые дают средние значение между среднечисловыми и среднемассовыми значения.

Во всех случаях используются эмпирические зависимости между молекулярными массами и свойствами растворов.

Например, для оценки значения средневязкостных молеку­лярных масс применяется степенное уравнение Марка- Ху­винка-Флори для так называемой характеристической вязкос­ти [η]:

[η]=KM_η^α , где К и α – эмпирические табличные константы.

[η]= lim η_уд/с, где η_уд- удельная вязкость (отношение вязкости раствора полимера к вязкости чистого растворителя, а с – концентрация.

Наиболее эффективным способом измерения ММР является метод гель-проникающей хроматографии. Он основыва­ется на хроматографировании раствора полимера на пористом носителе с различными размерами пор подходящим раствори­теле и детекторным определением каких-либо свойств раство­ра на выходе из колонки, пропорциональных молекулярной массе растворенного полимера.

Более надежные сведения о ММР дает толь­ко кривая ММР. Последнюю можно получить методами фрак­ционирования образца полимера на достаточно узкие по моле­кулярной массе фракции и последующего определения их средней молекулярной массы одним из описанных выше мето­дов. Применяются методы дробного осаждения полимеров из их растворов.

Термодинамика

Дата добавления: 2014-01-07