Общие сведения. Тема 3. Модели на основе теории Марковских процессов для определения оптимальных решений

Тема 3. Модели на основе теории Марковских процессов для определения оптимальных решений

Среди случайных процессов важное значение имеет так называемый марковский процесс, названный так в честь известного русского ученого Маркова А.А. (1856-1922).

Теория марковских случайных процессов впервые была изложена в книге академиком Колмогороввым А.Н. в 1936 году.

Случайный процесс называется марковским в том случае, если вероятность будущего состояния системы, отвечающей данному процессу, зависит только от ее состояния в настоящий момент времени и не зависит от того, в каких состояниях она была в прошлом. В связи с этим, марковские процессы называются процессами без последствия.

Марковский процесс называется процессом с дискретными состояниями, если переход системы из состояния в состояние совершается скачком, т.е. мгновенно. Типичным примером марковского случайного процесса с дискретными состояниями является работа транспортного средства. Марковские процессы с дискретными состояниями графически изображаются графом состояний. Так, например, если транспортное средство имеет две линии, то граф ее состояний можно представить рис. 1.

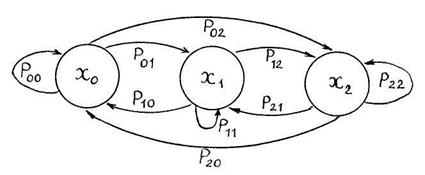
Рис. 11. Граф состояний дискретного марковского случайного процесса, если система имеет в своем распоряжении две линии: Х_о — состояние системы, когда обе линии свободны; вероятность этого состояния обозначается Р₀; Х₁ — состояние системы, когда занята одна линия; вероятность этого состояния обозначается Р₁; Х₂ — состояние системы, когда заняты обе линии; вероятность этого состояния обозначается Р₂; Р_ij — вероятность перехода системы из состояния в состояние.

Состояние системы характеризуется вектором состояний. Применительно к рис. 1 состояние системы в начальный момент времени при t = 0 запишется так:

.

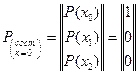Это значит, что в начальный момент времени система находится в состоянии Х_о вероятностью, равной единице.

Примечание. Как будет показано ниже, на основе вероятностей состояний системы определяются такие характеристики, как математическое ожидание числа занятых каналов, математическое ожидание длины очереди, математическое ожидание времени простоя в очереди и т.п., которые характеризуют эффективность функционирования системы в целом.

Заметим, что стрелками на рис. 1 показаны возможные переходы системы из ее состояния в состояние. Каждому переходу отвечает соответствующая вероятность Р_ij. Граф состояний, у которого нанесены численные значения вероятностей перехода, называется размеченным графом состояний системы.

Применительно к рис. 1 вероятности перехода системы из состояния в состояние могут быть представлены с помощью следующей матрицы

.

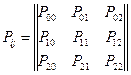Очевидно, что сумма вероятностей перехода в каждой строке равна единице. Момент перехода системы из состояния в состояние называют «шагами» процесса. Номер шага обозначают К (К = 0,1,2,3, n).

Последовательность состоянии системы Х_о, Х_1, Х_2… Х_n называют Марковской цепью, названной так по имени известного русского ученого Маркова А. А.

Марковская цепь называется однородной, если вероятности перехода Р_ij не зависят от номера шага. В противном случае марковская цепь называется неоднородной.

Марковский процесс называется процессом с дискретным временем, если переходы системы из состояния в состояние совершаются в строго определенные, заранее фиксированные моменты времени.

Марковский процесс называется процессом с непрерывным временем, если переходы системы из состояния в состояние возможен в любой, наперед неизвестный, случайный момент времени.

Дата добавления: 2014-01-07