Модели, описывающие системы массового обслуживания замкнутого вида

Наряду с открытыми системами в практике имеются так называемые закрытые, т.е. замкнутые системы. К ним относятся ремонтные мастерские, обслуживающие парки машин, например депо на балансе которых они находятся, строительно-дорожная техника данного строительного управления и т. п.

Отличительной особенностью замкнутых систем является то обстоятельство, что машины (заявки) в указанных системах не покидают очередь до тех пор, пока не будут обслужены. Это значит, что длина очереди или пропорциональное ей время пребывания в очереди не ограничивается заданным числом мест m, и можно считать что .

Для замкнутых систем выходящий поток каждой фазы является входящим для следующей фазы.

В связи с этим формула для определения вероятности Р. приобретает следующий вид

.

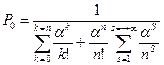Сумма во втором слагаемом в знаменателе представляет собой геометрическую прогрессию со знаменателем

.

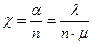Как известно, сумма членов геометрической прогрессии равна

.

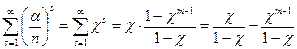Для установившегося режима (когда ) такое состояние системы может быть только при выполнении следующего условия:

Наличие указанного условия является следствием особенности рассматриваемого процесса, сущность которого состоит в том, что заявка, ставшая в очередь, рано или поздно будет обязательно обслужена.

Это значит, что выше указанная сумма представляет собой бесконечно убывающую прогрессию и второе слагаемое равно нулю

.

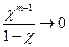С учетом этого, выражение для определения вероятности P₀ значительно упрос­тится и запишется так

Заметим, что при исследовании замкнутых систем массового обслуживания обычно решается не задача анализа, а задача синтеза оптимальных решений, т.е. определяют оптимальное количество ремонтных постов, при котором будет обеспечиваться оптимальный доход для заданного парка машин.

Для этого рассчитывают и строят график, на который наносят кривую удельных затрат на содержание заданного количества ремонтных постов (рис. 4, кривая № 1).

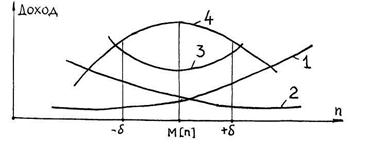
Рис. 4. Определение оптимального количества ремонтных постов для закрытых систем массового обслуживания

На указанный график наносят также кривую удельных затрат от простоя машин в ожидании ремонта (см. кривую № 2). Суммируя указанные кривые, получают суммарный график (см. кривую № 3). На график наносят также кривую удельного дохода (см. кривую № 4).

На основе построенного графика определяют в некоторых пределах (от — 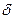до +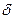) оптимальное количество ремонтных постов, при котором организация процесса с экономической точки зрения будет наилучшей. Этим самым решается задача по определению оптимального решения организации рассматриваемого технического процесса.

Дата добавления: 2014-01-07