Локальная формулировка второго начала термодинамики

Рассмотрим неравновесную систему, для каждого физически бесконечно малого элемента которой, определено значение плотности энтропии (6.1.3). В пределах каждого такого элемента выполняется условие детального равновесия, т.е. в каждой такой области энтропию можно определить термодинамически, через приведенное количество теплоты:

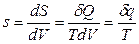, (6.2.1)

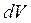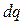где Т – температура, характеризующая объем , а - плотность количества теплоты.

Приращение плотности энтропии, аналогично приращению любой величины (например, плотности энергии (6.1.10)) можно разбить на две составляющие: 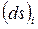- приращение плотности энтропии, обусловленное процессами внутри системы и 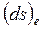- приращение, обусловленное процессами в окружающей систему среде:

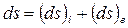(6.2.2).

По аналогии с рассмотрением плотности потока энергии, можно заключить, что скорость изменения плотности энтропии, обусловленная внешними процессами, равна дивергенции потока энтропии, взятой с обратным знаком:

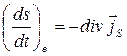. (6.2.3)

Об отличии или равенстве нулю производства энтропии в каждой точке системы (т.е. обусловленное процессами внутри системы) ничего определенного в общем случае сказать пока нельзя. Однако рассмотрев изменение энтропии в частных неравновесных процесса (например стационарном процессе теплопроводности) можно прийти к выводу что энтропия в каждой точке будет увеличиваться.:

Таким образом, в выражении (6.2.2) оба слагаемых отличны от нуля. И второе начало линейной термодинамики в локальной форме для рассматриваемого случая приобретает вид:

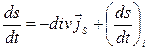(6.2.10)

Второе начало в виде (6.2.10) справедливо для неравновесной системы (не обменивающейся частицами), в которой коэффициенты переноса остаются постоянными. В таких условиях второе начало формулируется в виде: скорость изменения плотности энтропии равна сумме дивергенции потока энтропии, взятой с обратным знаком и скорости производства энтропии в данной точке системы.

На основе второго начала равновесной термодинамики получен критерий эволюции изолированных систем. Аналогично существует критерий эволюции систем в неравновесной термодинамике. Сейчас нам уже известно, что системы, не слишком удаленные от равновесия, при неизменных внешних условиях, переходят в стационарное состояние. Как при этом изменяется скорость производства плотности энтропии? Ответ на этот вопрос дает критерий эволюции Пригожина: процессы в системах, не слишком далеких от равновесия идут таким образом, что скорость производства плотности энтропии, в каждой точке системы, стремится к минимальной из всех возможных.

Этот вывод получен в научной школе И. Пригожина на основе анализа соотношений Онзагера, который занимался разработкой неравновесной термодинамики. За свои работы по неравновесной термодинамике в 1968 году Л. Онзагеру присуждена Нобелевская премия.

.

Дата добавления: 2014-01-07