Применение первого начала термодинамики к изопроцессам

Будем рассматривать квазиравновесные процессы, т.е. такие, которые идут настолько медленно, что характерное время установления внутреннего равновесия 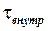много меньше времени наблюдения за протекающим процессом 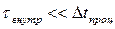. К таким процессам может быть применено первое начало термодинамики. Проанализируем с этой точки зрения квазиравновесные процессы в идеальном газе, то есть процессы в системах, уравнением состояния которых является уравнение Менделеева-Клапейрона.

Пусть процесс идет без теплообмена с окружающей средой, то есть система является адиабатически изолированной. Процессы происходящие в такой системе, называются адиабатными процессами, при этом 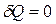. Для обеспечения этого условия процесс должен идти быстро. Противоречит ли это условию квазиравновесности процесса? Введем время установления равновесия системы с окружающей средой . О квазиравновесном адиабатном процессе можно говорить, только когда .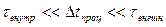

Предположим, что рассматриваемый процесс удовлетворяет указанному условию и, следовательно, к его анализу применимо первое начало термодинамики, которое в данном случае принимает вид

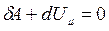, (3.3.1)

т.е. при адиабатном процессе работа совершается системой за счет убыли ее внутренней энергии, то

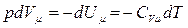. (3.3.2)

Теплоемкость системы в адиабатном процессе равна нулю. Это относится к термодинамической системе любой природы.

Получаем уравнение адиабаты через P и V

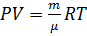продифференцируем

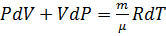или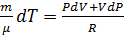

Только что получили

тогда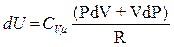

При адиабатическом процессе 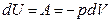тогда

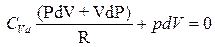умножим на Rи раскроем скобки

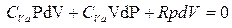
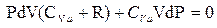разделим на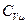

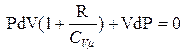(22)

Обозначим за и воспользуемся уравнением Майера 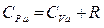откуда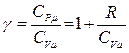

Тогда ур-е (22) перепишется

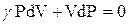Разделим переменные умножив на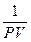

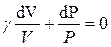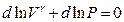или

или

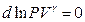
Проинтегрируем и получаем

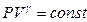- Уравнение адиабаты или уравнение Пуассона, где 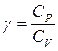- показатель адиабаты или коэффициент Пуассона

Уравнение адиабаты можно получить через другие параметры, например V,T

Согласно уравнению Менделеева - Клайперона

P~T/V

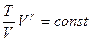
Тогда приходим к уравнению адиабаты в координатах (V,T), связывающему температуру и объем идеального газа в адиабатном процессе:

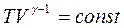, (3.3.4)

Аналогично

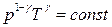. (3.3.6)

Найдем выражение для работы, совершаемой идеальным газом в адиабатном процессе при переходе из состояния 1 с параметрами 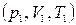в состояние 2 c параметрами .

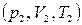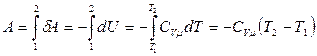. (3.3.7)

Поскольку численное значение работы и ее знак удобно определять по графику процесса, изображенного в координатах 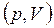, адиабату часто изображают именно в этих координатах. На рис. 3.3.1 изображены изотерма и адиабата для равных масс идеального газа.

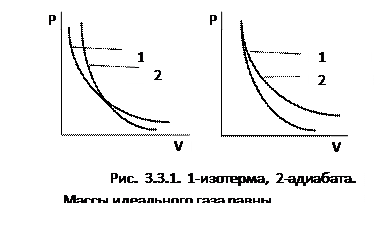Большая крутизна адиабаты по сравнению с изотермой может быть объяснено из термодинамических представлений. Пусть изотермическое и адиабатное расширение начинаются из одного и того же состояния. В изотермическом процессе давление уменьшается за счет уменьшения объема, а в адиабатном процессе – за счет уменьшения объема и уменьшения средней кинетической энергии молекул, то есть быстрее, чем в изотермическом процессе. Рассуждая аналогично в случае начала изотермического и адиабатного сжатия из одного и того же состояния, приходим к выводу, что увеличение давления в адиабатном процессе идет медленнее.

Можно показать, что теплоемкость в изотермическом процессе равна бесконечности

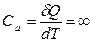при T = const, (3.3.8)
при постоянном давлении и при постоянном объеме теплоемкости имеют некоторые конечные значения

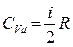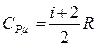, , (3.3.9)
в адиабатном процессе теплоемкость равна нулю, т.к. .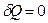

Рассмотрим теперь процессы с промежуточными значениями теплоемкости, которая в течение процесса не изменяется 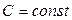. Процессы, идущие при постоянной теплоемкости, называются политропическими процессами. Пусть адиабатный процесс, совершаемый над одним молем идеального газа является квазиравновесным.

Согласно первому началу термодинамики для рассматриваемого случая получаем

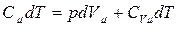, (3.3.10)
где 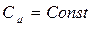при политропических процессах. С учетом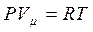

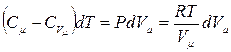, откуда .

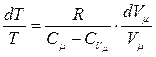Из уравнения Майера 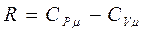, следовательно

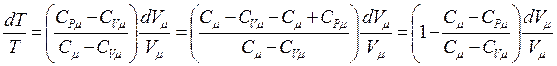
Величина 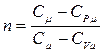называется показателем политропы. Тогда

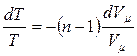. (3.3.11)

Интегрируя правую и левую части (метод разделения переменных), получим

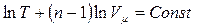или

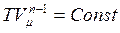(3.3.12)

- уравнение политропы. С помощью уравнения Менделеева-Клапейрона его можно записать в виде:

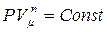. (3.3.13)

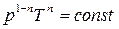. (3.3.14)

Очевидно, что

при С = 0; n = γ; 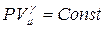— уравнение адиабаты;

при С = ∞; n = 1; 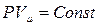— уравнение изотермы;

при С = С_р; n = 0; P = Const — уравнение изобары;

при C = C_v; n = 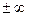; 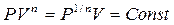, но 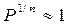, следовательно, V = Const — уравнение изохоры.

Все изопроцессы являются частными случаями политропического процесса.

Дата добавления: 2014-01-07