Теплоемкость идеальных газов

Нами уже была установлена связь между теплоемкостями идеального газа, или любого газа вообще, при постоянном давлении и при постоянном объеме (3.2.11). Таким образом, достаточно определить одну из теплоемкостей, а вторая определится из уравнения Майера. Проще найти выражения для теплоемкости при постоянном объеме.

Определим молярную теплоемкость идеального газа при постоянном объеме, взятого в количестве 1 моль (что не нарушит общности). Чтобы найти ее, необходимо задать вид зависимости внутренней энергии от температуры. Выше установлено, что для идеального газа, с точностью до постоянной, внутренняя энергия равна

, (3.6.1)

где 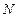- число молекул газа.

Согласно теореме о равнораспределении кинетической энергии по степеням свободы

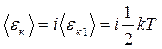. (3.6.2)

Здесь - кинетическая энергия, приходящаяся на одну степень свободы.

Средняя кинетическая энергия молекул идеального газа определяется как (1.4.33) . Однако этот вывод получен в предположении, что молекулы можно считать материальными точками, которые имеют три степени свободы. В этом случае элементарное приращение внутренней энергии одного моля идеального газа равно , а молярная теплоемкость при постоянном объеме равна . При обычных температурах экспериментальные значения молярной теплоемкости при постоянном объеме для гелия и аргона совпадают с теоретическими значениями . Однако для азота, кислорода, водорода, экспериментальные значения при обычных условиях больше предсказываемых теоретических значений примерно на величину универсальной газовой постоянной. Чтобы объяснить расхождение экспериментальных и теоретических результатов, пришлось отказаться от представления о молекулах как о материальных точках.

Рассмотрим двухатомную молекулу. Пусть связь атомов в молекуле жесткая, то есть расстояние между атомами не изменяется. Такую систему можно считать абсолютно твердым телом, любое движение которого может быть представлено в виде суперпозиции поступательного движения центра масс и вращательного движения вокруг свободных осей (если не наложены связи). То есть у незакрепленного абсолютно твердого тела три поступательные и три вращательные степени свободы. Так как момент инерции двухатомной молекулы относительно ее оси симметрии пренебрежимо мал, то вращением относительно этой оси можно пренебречь и считать, что жесткая двухатомная молекула имеет три поступательные и две вращательные степени свободы. И молярная теплоемкость при постоянном объеме равна

. (3.6.3)

Итак, по классической теории выражения для молярных теплоемкостей идеального газа имеют вид

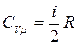, (3.6.4)

(3.6.5)

и не зависят от температуры.

Если связь атомов в молекуле не жесткая, то возможно колебательное движение внутри молекул, то есть появляются колебательные степени свободы. Расчет числа колебательных степеней свободы можно выполнить следующим образом: если считать, что каждый атом привносит в молекулу 3 степени свободы, а в молекуле N атомов, то всего получается 3N степеней свободы. Из них 3 степени свободы определяют поступательное движение молекулы как целого, 3 (или 2 в случае двухатомной молекулы) - вращательное движение молекулы как целого, а остальные определяют колебательные степени свободы

(3.6.6)

В привычных условиях теоретические значения теплоемкостей совпадают с экспериментальными. Однако для широкого диапазона температур была обнаружена зависимость теплоемкости от температуры. На рис. 3.6.1 приведена экспериментальная температурная зависимость теплоемкости водорода.

Рис. 3.6.1. Экспериментальная зависимость теплоемкости водорода от температуры

Классическая теория теплоемкости не может объяснить температурную зависимость теплоемкости газа. Можно только сказать, что двухатомный водород в некоторой области температур ведет себя как одноатомная молекула: вклад в теплоемкость дают только поступательные степени свободы, в следующем температурном интервале включаются вращательные степени свободы, и молекула водорода ведет себя как жесткая двухатомная молекула. При высоких температурах работают и поступательные, и вращательные, и колебательные степени свободы, молекула водорода «становится» упругой двухатомной молекулой. Но это всего лишь констатация факта, а не объяснение экспериментальной закономерности, которое может дать только квантовая теория теплоемкости.

На качественном уровне это может быть интерпретировано следующим образом: Согласна квантовой физике энергия, которой может обладать микрочастица квантована. Т.е она может принимать только ряд значений (говорят есть уровни энергии). Причем для поступательного, вращательного и колебательного движение значение и плотность этих уровней различная.

Дата добавления: 2014-01-07