Динаміка безперервних екстремальних систем

Для характеристики якості роботи системи звичайно використовують такі показники (рис. 11.12):

- параметри автоколивань у зоні екстремуму: період Т_а і амплітуда а, причому розмах коливань DІ називається зоною пошуку на виході, а розмах коливань Du – зоною пошуку на вході;

- різниця між екстремальним І^* і середнім І_сер значеннями критерію на виході об’єкта, яка називається втратою на пошук Р, що характеризує точність роботи системи;

- час Т₀ виходу системи з початкового стану І₀ у зону екстремуму, що характеризує швидкодію системи.

Розглянемо деякі методи розрахунку показників якості СЕК.

Знехтуємо спочатку інерційністю об’єкта керування (Т₁»Т₂»0). Тоді функціональна схема СЕК із вимірюванням знака похідної буде мати вигляд, наведений на рис. 11.13, а.

Обчислювальний пристрій (ОП) визначає похідну dI/du, яка подається на вхід релейного елемента (РЕ) і далі - на вхід виконавчого механізму (ВМ), що працює з постійною швидкістю v₀. Статична характеристика об’єкта апроксимується параболою:

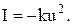(11.11)

Оскільки РЕ має характеристику, еквівалентну петльовій, у системі встановляться симетричні відносно точки екстремуму автоколивання. Визначимо основні показники якості роботи системи для даного випадку (рис. 11.13, б).

Зони пошуку екстремуму на вході й на виході визначаються таким чином.

Маємо 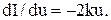З іншого боку, в момент подання команди на реверс де D - зона нечутливості РЕ. Отже, у цей момент 2ku_a = D, u_a = D/2k, а зона пошуку на вході буде:

Du = 2u_a = D/k. (11.12)

Зону пошуку на виході з урахуванням (11.11) визначимо з виразу:

DI = I^* - I(u_a) = 0 – [(-k)× D²/(2k)²] = D²/(4k). (11.13)

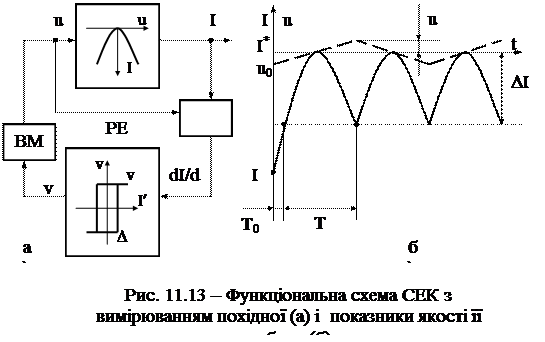
Тут ураховано, що при статичній характеристиці (11.11) екстремальне значення критерію I^* дорівнює нулю.

Період автоколивань Т_а з урахуванням того, що u = v₀t, визначимо зі співвідношення:

u_a = D/2k = v₀Т_а/2; звідки Т_а = D/(v₀k). (11.14)

Визначимо втрати на пошук:

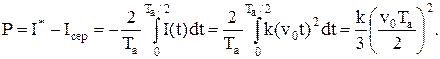
Тоді з урахуванням (11.13) і (11.14) маємо:

(11.15)

Час виходу системи у зону екстремуму з урахуванням (11.12):

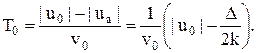(11.16)

Як випливає з отриманих виразів, збільшення D призводить до збільшення втрат на пошук Р і зони пошуку на виході DІ, тобто до погіршення точності роботи системи.

Підвищення швидкості виконавчого механізму v₀ зменшує період автоколивань Т_а і час Т₀. На якісні показники роботи системи впливає і крутість статичної характеристики, яка визначається коефіцієнтом k: збільшення k знижує величини Р і DІ.

Розглянемо об’єкти, що мають інерційність. Нехай об’єкт має структуру, що наведена на рис. 11.11, б. Тоді рівняння ланок СЕК з пропорційним керуванням (рис. 11.14) можна записати у вигляді:

- лінійна частина об’єкта (ЛЧ)

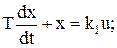(11.17)

- нелінійна частина об’єкта

(11.18)

- екстремальний регулятор (ЕР)

(11.19)

- виконавчий механізм (ВМ)

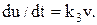(11.20)

Розв’язавши цю систему рівнянь, отримаємо:

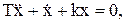(11.21)

де k=2k₁k₂k₃.

Рівняння (11.21) є лінійним диференціальним рівнянням, і подальший аналіз перехідних процесів у системі можна виконувати звичайними методами лінійної теорії автоматичного керування.

Наприклад, при 4kT > 1, що відповідає коливальній ланці (x<1), розв’язок рівняння (11.21) має вигляд:

(11.22)

де 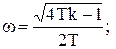А і j - сталі інтегрування.

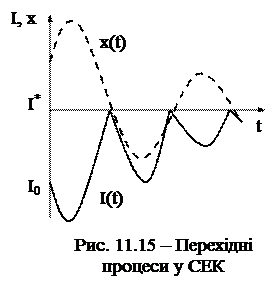
На рис. 11.15 наведені залежності x(t) і I(t), обчислені за формулами (11.22) і (11.18). З рисунку видно, що при ступінчастому збуренні (І = І₀) система здійснює загасаючі коливання навколо екстремальної точки (І^*=0).

Зона пошуку на виході DІ а, отже, втрати на пошук Р у даній системі в усталеному режимі дорівнюють нулю.

У разі використання для керування виконавчим механізмом релейного елемента рівняння системи матиме вигляд:

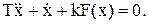(11.23)

Тут ураховано, що рівняння (11.19) з урахуванням (11.18) являє нелінійну залежність вигляду: v = F(x).

Рівняння (11.23) є нелінійним, і його можна дослідити за допомогою нелінійної теорії автоматичного керування.

Нехай тепер об’єкт має структуру (рис. 11.11, в), а екстремальний регулятор здійснює пошук із запам’ятовуванням екстремуму (рис. 11.16). Рівняння окремих ланок мають вигляд:

- лінійна частина об’єкта (ЛЧ)

(11.24)

- нелінійна частина об’єкта

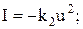(11.25)

- виконавчий механізм (ВМ)

(11.26)

- екстремальний регулятор (ЕР)

(11.27)

Сумісний розв’язок рівнянь об’єкта (11.24) і (11.25) дає:

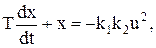або

а з урахуванням (11.26) отримаємо:

Позначимо: 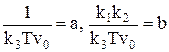, тоді з урахуванням, що 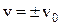, маємо:

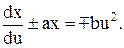(11.28)

Отримане рівняння є диференціальним рівнянням фазової траєкторії у координатах “вхід об’єкта u – його вихід х ”. Нехай початкове значення координат об’єкта буде u₀, x₀=k₁I₀ (рис. 11.17, а) і при цьому v₀>0. Якщо об’єкт безінерційний, то x=k₁I і фазова траєкторія х(u) при k₁=1 співпадає зі статичною характеристикою I(u). У разі наявності інерційності рівняння фазової траєкторії є розв’язком рівняння (11.28):

(11.29)

Сталу С визначимо з початкових умов при t=0: u = u₀, x = x₀. Тоді:

(11.30)

Відповідно до (11.29) на рис. 11.17,а побудовано фазову траєкторію х=f(u). Після того, як фазова траєкторія перетне статичну характеристику об’єкта, координата х почне зменшуватись, отже, знак Dх буде від’ємним. Це видно з рівняння лінійної частини об’єкта (11.24): при k₁=1, , отже, при І = х похідна dx/dt змінює свій знак, значить, у цій точці значення х максимальне.

При 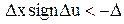(точка 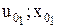) релейний елемент спрацьовує і відбувається реверс ВМ. Рівняння фазової траєкторії зберігає той самий вигляд, однак, оскільки у даному випадку v₀<0, то коефіцієнти a і b у рівняннях (11.29) і (11.30) змінюють свій знак, а до (11.30) також замість 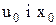необхідно підставити 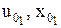. У точці знову відбудеться реверс і т.д.

Граничний цикл (безперервна лінія на рис. 11.17, а) характеризує усталені симетричні автоколивання у системі.

За фазовою траєкторією і граничним циклом можна визначити якісні показники системи.

Зона пошуку на вході дорівнює 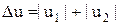, а на виході визначається різницею між мінімальним і максимальним значеннями вихідного параметра х, тобто Dх = х₁ - х₂ = 2D. Період автоколивань, з урахуванням того, що швидкість виконавчого механізму дорівнює k₃v₀, можна визначити зі співвідношення:

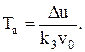
Оскільки автоколивання симетричні, то втрати на пошук будуть:

Час виходу до екстремуму визначимо як суму інтервалів часу, за які система проходить певні ділянки фазової траєкторії:

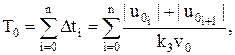
де n – кількість ділянок фазової траєкторії до виходу на граничний цикл.

Приклад 11.3 Нехай об’єкт керування описується рівнянням

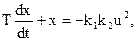
а рівняння виконавчого механізму з урахуванням екстремального регулятора з релейним елементом має вигляд:

Значення параметрів: Т = 1 с; k₁ = k₂ = 1; v₀ = 1; k₃ = 1c^-1; D=0,2.

Визначити період автоколивань і втрату на пошук.

Знаходимо координати точок реверсу А(u_a, x_a) і B(u_b,x_b).

Записуємо рівняння (11.29) з урахуванням (11.30) для додатного (v₀>0) півциклу автоколивань для точки В (рис. 11.18). Коефіцієнти a і b для заданих параметрів системи дорівнюють одиниці. Тоді отримуємо:

Ураховуючи, що при усталених автоколиваннях x_a = x_b і u_b = -u_a, визначимо з отриманого виразу x_b:

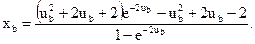(11.31)

Друге рівняння, що зв’язує координати x_b і u_b, отримаємо так. Оскільки k₁ = 1, то точка С, що відповідає максимальному значенню х, лежить на статичній характеристиці. Отже,

(11.32)

звідки знаходимо:

(11.33)

Запишемо (11.29) для точки С:

З урахуванням (11.32) і (11.33) отримаємо:

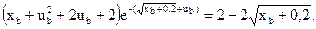(11.34)

З рівнянь (11.31) і (11.34) можна визначити шукані x_b і u_b. Оскільки отримана система є трансцендентною, розв’язати її можна чисельними або графічними методами.

Результати розрахунків для даного прикладу такі: u_b = 1, x_b = -0,4. Період автоколивань Т_а = 2u_b/(k₃v₀) = 2 c; втрати на пошук складають P = I^* - x_b = 0,4.

Дата добавления: 2014-01-07