Принципы группового выбора

Принципы группового выбора определяют согласование индивидуальных предпочтений в групповом предпочтении и, следовательно, по существу являются критериями выбора оптимального решения. Пусть F(f) – функция группового предпочтения, зависящая от вектора индивидуальных предпочтений f = (f₁, f₂,..., f_d), где d — количество членов в групповом ЛПР. Выбор конкретного принципа согласования позволяет построить явный вид функции группового предпочтения. Рассмотрим ряд принципов согласования и соответствующие им функции группового предпочтения.

Принцип диктатора - П₁

В соответствии с этим принципом в качестве группового предпочтения принимается предпочтение одного лица группы – диктатора. Следовательно, функция группового предпочтения равна функции предпочтения диктатора f_k

(62)

Ввиду того, что при данном принципе совершенно не учитываются предпочтения других членов группы, понятие группового ЛПР теряет содержательный смысл. По существу групповое предпочтение в данном случае соответствует индивидуальному предпочтению.

Принцип большинства – П₂

В групповом ЛПР могут образовываться коалиции – объединения членов группы о совпадающими целями. Пусть в групповом ЛПР возникло множество коалиций V = (V₁, V₂,..., V_s), где s – количество коалиций. При s = d все коалиции одноэлементные, т.е. включают только по одному члену и, следовательно, все члены группы преследуют разные цели. При s = 1 имеет место всего одна коалиция, включающая всех членов группового ЛПР и преследующая одну или несколько общих целей. В промежуточном случае 1 < s < d образуется конечное число коалиций.

Каждая коалиция имеет свою функцию предпочтения f_Vk. При измерении предпочтений в качественных шкалах объединение индивидуальных предпочтений в коалиционное предпочтение обычно осуществляется по принципу 100% большинства, т.е. одно решение предпочитается в коалиции другому, если все члены коалиции имеют такое же предпочтение. При измерении предпочтений в количественных шкалах коалиционное предпочтение обычно получают как взвешенную сумму индивидуальных предпочтений членов коалиции

(63)

где 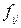– индивидуальное предпочтение i -го индивида в j -й коалиции, k_i – коэффициенты весов членов коалиции; суммирование производится по всем номерам членов i, входящих в j -ю коалицию.

Таким образом, каждая коалиция характеризуется своей функцией предпочтения, а все множество коалиций, входящих в групповое ЛПР, характеризуется вектором функции предпочтения f = (fV₁,..., fV_s).

Обозначим через П_Vj – количество членов, входящих, в коалиции V_j. Очевидно, что П_V1 + П_V2 +... + П_Vs = d, т.е. сумма членов, входящих во все коалиции, равна количеству членов группового ЛПР.

Принцип большинства утверждает, что групповое предпочтение должно соответствовать предпочтению коалиции, которая имеет число членов (голосов), превышающих некоторый порог, формально это можно записать в виде

, при П_Vk > C d/2 (64)

где f_Vk – функция предпочтения коалиции, имеющей число голосов П_Vk, С – некоторый коэффициент, изменяющийся в пределах 1£ С£ 2. При С = 1 порог равен половине членов группового ЛПР, поэтому говорят о принципе простого большинства голосов. При С = 4/3 порог равен 2/3 голосов, поэтому говорят о принципе большинства в 2/3 голосов, при С = d порог равен d, что соответствует абсолютному большинству голосов.

При измерении предпочтения в качественных шкалах определение группового предпочтения, соответствующего принципу большинства голосов, осуществляется путем нахождения медианы индивидуальных ранжирований или парных сравнений. Медиана групповой экспертной оценки соответствует принципу большинства голосов.

Принцип большинства голосов используется при демократическом способе принятия решений. Принцип диктатора характерен для военных организаций и широко пользуется при принятии в чрезвычайных обстоятельствах.

Принципы диктатора и большинства голосов не учитывают интересы всех индивидов группы. Их применение при отсутствии других сдерживающих факторов может привести к распаду группового ЛПР. В формулировке этих принципов не содержится оснований для обеспечения устойчивости существования группы.

Существуют принципы согласованности индивидуальных предпочтений, обеспечивающее в некотором смысле учет интересов всех членов группы, и, следовательно, сохраняющие ее устойчивость.

Пусть имеется множество коалиций V = (V₁, V₂,..., V_s), s £ d, где d – количество членов в группе. Решение называется V - оптимальным, если оно оптимально для всей коалиции.

V - оптимальность означает, что ни одной коалиции не выгодно менять этого решения, поскольку не существует лучшего времени. Рассмотрим конкретный принцип согласования, основанный на понятии V - оптимальности - принцип Парето.

Пусть множество коалиций состоит из одной коалиции, т.е. все члены группового ЛПР образуют единое целое, V - оптимальное решение в этом случае соответствует принципу Парето. Всем членам группы сразу невыгодно менять оптимального по принципу Парето видения, поскольку не существует лучшего. Принцип Парето выражает некоторый гуманистический идеал: все члены группы могут улучшать свои решения без нанесения ущерба другим членам. применение принципа Парето возможно только при сильной зависимости всех членов группового ЛПР. Эта зависимость выражается в общности целей всех членов группы.

Множество эффективных решений удовлетворяет принципу Парето, поэтому этот принцип широко используется в задачах выбора. Учитывая практическую важность этого принципа, он подробно рассмотрен в следующем параграфе.

Конкретизация принципов согласования может быть произведена на основе рассмотрения характера отношений между коалициями группового ЛПР. Рассматривается три типа отношений между коалициями: статус-кво, конфронтация и рациональность.

При отношении статус-кво предполагается бездействие коалиций, они стараются сохранить существующее положение. Это отношение используется в экономических моделях, в которых рассматриваются взаимодействия слабо связанных участков. Рассмотрим, какой вид будут иметь функции группового предпочтения в условиях отношения статус-кво

(65)

Функция группового предпочтения равна вектору индивидуальных предпочтений, такому, который при решении Y^* не хуже в векторном смысле, чем при любом другом решении.

Векторное отношение «не хуже» означает, что один вектор предпочтительнее другого, воли все компоненты первого вектора не хуже соответствующих компонент другого вектора и, по крайней мере, одна компонента первого вектора строго лучше, чем соответствующая компонента второго вектора. Очевидно, что решение Y^* не хуже решения Y₁ для всех членов сразу, т.е. они образуют единственную коалицию, что и должно быть в условиях принципа Парето. Принцип Парето используется при выборе решений, оцениваемых по многим показателям.

Дата добавления: 2014-01-07