Определение эффективных решений

Как уже отмечалось, выбор решений производится последовательными фазами. Вначале из исходного множества решений определяется подмножество допустимых решений, удовлетворяющих сформулированным ограничениям. Затем из множества допустимых решений определяется подмножество эффективных решений и, наконец, из этого подмножества выбирается единственное решение. Рассмотрим более подробно определение множества эффективных решений.

Определение множества эффективных решений основывается на использовании принципа Парето. Пусть имеется множество допустимых решений Y_Д = (Y₁, Y₂,..., Y_m) и групповое ЛПР, включающее членов. Каждый член группового ЛПР оценивает предпочтения решений в виде значения функции предпочтения f_s(Y_i), где s – номер члена группового ЛПР, Y_i – i -тое решение из множества допустимых решений. В соответствии с принципом Парето одно решение предпочитается другому, если вектор, составленный из функций предпочтения членов группового ЛПР для одного решения, не хуже, чем тот же вектор предпочтения для другого решения. Следовательно, Y_i Y_j, если

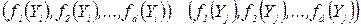(66)

Записанное соотношение является векторным отношением «не хуже» т.е. векторным квазипорядком. Выполнение этого векторного отношения означает, что все члены группы оценили решение Y_i не хуже решения Y_j, по крайней мере, один член группового ЛПР высказался за строгое предпочтение решения Y_i по сравнении с решением Y_j. формально это условие можно записать в виде неравенств:

(s ¹ k, s, k = 1, 2,..., d) (67)

Множество эффективных решений определяется путем сравнения всех решений по предпочтениям на основе соотношения (67). Те решения, для которых выполняются эти соотношения, образуют множество эффективных решений, часто их называют множеством Парето или множеством недоминируемых решений. Слово недоминируемых непосредственно вытекает из условий (67), поскольку не существует лучших (доминирующих) решений, чем множество эффективных.

Множество эффективных решений обладает следующими свойствами:

1. Любые два эффективных решения являются недоминирующими по отношению друг к другу.

2. Для любого решения, не принадлежащему множеству эффективных решений, всегда найдется, по крайней мере, одно эффективное решение, которое его доминирует.

Перечисленные свойства множества эффективных решений приводят к следствию: оптимальное решение находится среди эффективных решений. Таким образом, определив множество эффективных решений, достаточно в дальнейшем рассматривать только это множество для нахождения оптимального решения, отбросив все решения, не являющиеся эффективными.

Следует подчеркнуть, что не все эффективные решения являются строго лучшими, чем неэффективные решения. Какое-либо эффективное решение может быть эквивалентным некоторому неэффективному решению. Однако, в соответствия со свойством (67) во множестве эффективных решений найдется обязательно хотя бы одно лучшее решение для любого неэффективного решения. Это утверждение будет далее проиллюстрировано в примере.

Определение множества эффективных решений позволяет в большинстве случаев сузить множество допустимых решений, т.е. в множестве эффективных решений будет меньше количество решений, что облегчает дальнейшую задачу определения единственного оптимального решения. Количественно степень этого сужения оценивается коэффициентом определенности выбора, вычисляемого по формуле

(68)

где m_д – количество решений в допустимом множестве (мощность множества допустимых решений), m₀ – количество эффективных решений (мощность множества эффективных решений). Если множество эффективных решений содержит только одно решение, т.е. m₀ = 1, то коэффициент определенности выбора равен единице. Действительно, единственное эффективное решение является оптимальным решением, поэтому определенность выбора полная. Если в множестве эффективных решений содержится столько же решений, как и в исходном допустимом множестве, т.е. m₀ = m_Д, то из формулы (68) следует g = 0 – определенность выбора нулевая, поскольку никакого сужения множества допустимых решений не произошло. В промежуточных случаях, когда 1 < m₀ < m_Д, коэффициент определенности выбора изменяется в интервале 0 < g < 1. Коэффициент определенности выбора является характеристикой полезности выделения множества эффективных решений. При g = 1 эта полезность идеальная – найдено сразу оптимальное решение. При g = 0 выделение эффективных решений ничего не дало о точки зрения выбора единственного решения.

Существует ряд методов определения множества эффективных решений. Среди этих методов можно отметить метод прямого перебора и метод линейных форм. Метод линейных форм позволяет уменьшить объем вычислений по сравнению с перебором. Метод прямого перебора заключается в непосредственном сравнении предпочтений всех членов группового ЛПР в соответствии с неравенствами (67). Метод прямого перебора применим при небольшом количестве решений и членов группового ЛПР. Если в множестве допустимых решений содержится m_д – решений и количество членов в групповом ЛПР равно d, то необходимо произвести m_Д (m_Д - 1) d/1 сравнений. Если, например m_Д = 10 и d = 8, то необходимо сравнить 360 чисел, что практически реализуемо только на ЭВМ.

Пример 6. Пусть имеется четыре допустимых решения Y₁, Y₂, Y₃, Y₄. В групповом ДПР икается два члена с функциями предпочтения f₁ и f₂. Оба ЛПР проранжировали решения следующим образом: Y₂ £ Y₃ £ Y₁ £ Y₄; Y₃ £ Y₁ £ Y₂ ~ Y₄.

Удобно для наглядности представить все решения в системе координат на рис.41. По оси f₁ отложены предпочтения первого ЛПР, а по второй оси — предпочтения f₂ второго члена группового ЛПР. Каждое решение характеризуется двумя координатами, представляющими собой ранги, проставленные первым и вторым ЛПР.

Рис. 41. Представление решений в системе координат

Ранги по осям расположены так, что чем дальше от начала координат расположены решения, тем они предпочтительнее.

Используя неравенства (67), убеждаемся, что множество эффективных решений включает решения Y₂ и Y₃. Действительно, оба эти решения не доминируют друг друга, поскольку первый ЛПР предпочел Y₂ ³ Y₃, а второй наоборот: Y₃ ³ Y₂. Оба решения, т.е. (Y₃, Y₂) > (Y₁, Y₄). Решение Y₃ строго предпочтительнее решений Y₁ и Y₄, поскольку оба члена группового ЛПР дают решению Y₃ более высокий ранг, чем решениям Y₁ и Y₄. Решения Y₁ и Y₂ несравнимы между собой, так как первый ЛПР считает Y₂ ³ Y₁, а второй наоборот: Y₁ ³ Y₂. Решение Y₂ доминирует решению Y₄, т.е. Y₂ > Y₄ поскольку первый ЛПР считает Y₂ ³ Y₄, а второй считает их эквивалентными Y₂ ~ Y₄. Коэффициент определенности выбора в данном примере равен .

Задачи многокритериального выбора (векторной оптимизации) являются частными случаями задачи группового выбора. В этих задачах роль группового ЛПР выполняет совокупность независимых показателей решений. Пусть имеется множество допустимых решений Y_д= (Y₁, Y₂,..., Y_m) и множество показателей y₁, y₂,..., у_q. В качестве показателей могут использоваться, например, показатели степени достижения целей, стоимость, прибыль и другие технико-экономические характеристики решений. Для каждого i -го решения определяется вектор значений показателей (y_i1, y_i2,..., y_iq). В соответствии с принципом Парето одно решение Y_i предпочтительнее другого решения Y_j, если выполняется векторное отношение «не хуже»

(y_i1, y_i2,..., y_iq) ³ (y_j1, y_j2,..., y_jq) (69)

Выполнение векторного отношения «не хуже» означает выполнение неравенства

y_ik ³ y_jk, y_il > y_jl, (k ¹ l, k = 1, 2,..., q) (70)

Значения у_ik есть предпочтение k -й характеристики i -го решения.

Изложенное показывает, что задача выбора одним ЛПР множества эффективных решений по многим показателям формально ни чем не отличается от задачи выбора эффективных решений по одному показателю множеством членов группового ЛПР. Просто роль членов ЛПР играют показатели решений.

Рассмотрим теперь общий случай, когда имеется групповой ЛПР, включающий d членов, и оценка множества решений производится по совокупности q показателей. В этом случае решение Y_i, предпочтительнее решения Y_j, если выполняются следующие неравенства:

,

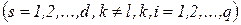(71)

где f_s(у_ik) – функция предпочтения s -го члена группового ЛПР, у_ik – значения k -го показателя для i -го решения.

Пример 7. Для иллюстрации определения множества эффективных решений при нескольких показателях рассмотрим следующую задачу выбора. Пусть сформулировано множество допустимых вариантов плана реконструкции предприятия, содержащее 6 решений (планов). Каждый план реконструкции оценивается по прибыли – у_i1 и величине капитальных вложений – y_i2, (в действительности план реконструкции оценивается большим числом технико-экономических показателей, и выбор только двух показателей связан с упрощением задачи с целью ее наглядности). Все решения отдельно по прибыли и по капвложениям проранжированы. Результаты ранжирования решений представлены в табл. 19.

Из таблицы следует, что по прибыли решения упорядочены следующим образом:

Y₁ > Y₃ > Y₂ > Y₅ > Y₄ > Y₆ (72)

Таблица 27

	Y1	Y2	Y3	Y4	Y5	Y6
yi1
yi2

По капитальным вложениям решения упорядочены по предпочтению следующим образом (вторая строка рангов в таблице):

Y₃ > Y₁ > Y₅ > Y₂ > Y₆ > Y₄ (73)

Представим каждое решение как точку на плоскости с осями координат, соответствующих прибыли и капвложениям (рис. 11).

Рис. 11. Представление решений на плоскости с осями координат

На осях координат отложены ранги таким образом, что по мере удаления от начала координат предпочтения увеличиваются, т.е. по оси у_i1 увеличивается прибыль, а по оси у_i2 уменьшаются капвложения. Покажем, что решения Y₁ и Y₃, составляют множество эффективных решений. Действительно, каждое из этих решений предпочтительнее других решений Y₂, Y₄, Y₅, Y₆ как по прибыли, так и по капвложениям одновременно. Сами эффективные решения Y₁, Y₃ между собой несравнимы, поскольку решение Y₁, предпочтительнее решения Y₃ по прибыли, но уступает ему по показателю капвложений. Поскольку эти два показателя "между собой не сравниваются и являются, следовательно, независимыми, то отдать какое-либо предпочтение одному из эффективных решений в рамках располагаемой информации нельзя.

Коэффициент определенности выбора в рассматриваемом примере, в соответствии с формулой (68), равен

у =(6-2)/(6-1) =4/5 =0,8

Для выбора единственного решения на реконструкцию достаточно рассматривать только эффективные решения Y₁ и Y₃. Если ЛПР может высказать предпочтения о сравнительной значимости прибыли и затрат на капвложения, то однозначно определится единственное решение: либо Y₁, либо Y₃.

Графическое представление на рис. 11 процедуры определения множества эффективных решений подсказывает общую схему расчетов. Если имеется мерный вектор характеристик решений, то рассматривается q -мерное пространство с осями координат по каждой характеристике. При условии разметки осей с увеличением предпочтительности при удалении от начала координат наилучшие решения, как точки в q -мерном пространстве будут расположены в «северо-восточном» углу, т.е. наиболее удалены от начала координат. Сравнением характеристик производится отбор решений, входящих во множество эффективных решений. Эта процедура легко реализуется на ЭВМ.

Рассмотренный пример иллюстрирует решение задачи многокритериального выбора. В данном случае каждое решение описывалось только двумя показателями (критериями). Технология построения множества эффективных решений для случая многих показателей (характеристик) решений аналогична.

Пример 8. Рассмотрим задачу сравнительной оценки деятельности предприятий. Такая задача систематически решается в отраслях и объединениях при подведении итогов производственно-экономической деятельности за определенный период времени (год, пятилетка). Пусть имеется n предприятий, деятельность которых оценивается m показателями. Имеются данные по значению всех показателей для каждого предприятия. Требуется упорядочить предприятия по множеству значений показателей. На основе этого упорядочения принимаются решения о поощрении их руководителей и сотрудников, проходится анализ причин недостатков в отстающих предприятиях.

Данную задачу можно интерпретировать как последовательное определение множества эффективных решений. Действительно, все предприятия можно рассматривать как множество допустимых решений, каждое из которых характеризуется вектором значений показателей. Определим множество эффективных решений, т.е. множество недоминирующих по всем показателям предприятий, и исключим их из списка. Затем для оставшегося множества решений (предприятий) вновь определим подмножество эффективных решений и опять исключим их из списка. Повторяя эту процедуру до тех пор, пока сужение множества решений до эффективного происходить не будет, т.е. последнее допустимое множество не будет совпадать с эффективным, мы получим полное упорядочение множества решений (предприятий).

Пусть имеется 17 предприятий, именуемых П₁, П₂,..., П₁₇, деятельность которых оценивается по пяти показателям. Значения показателей по каждому предприятию приведены в табл. 28. Причем значения показателя даются в физических единицах, а затем переводятся в ранги. В таблице физические единицы (в рублях) приведены только для показателя производительности труда (первая колонка). Перевод значений показателей в ранги не вызывает каких-либо трудностей. Первый ранг приписывается наилучшему значению показателя, второй ранг – следующему после наилучшего и т.д. Необходимость перевода значений показателей в ранги определяется простотой дальнейшей обработки и не влияет на точность решения задачи, поскольку в конечном итоге требуется только упорядочение объектов, т.е. оценка объектов в рангах.

При условии, что все пять показателей независимы и равноценны, на ЭВМ было выполнено последовательное выделение множеств эффективных решений на основе условий (5). В результате построено следующее упорядочение предприятий

(П₁, П₃, П₅, П₁₀, П₁₆) (П₂, П₄, П₇, П₁₂, П₁₅)

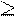(П₉, П₁₁, П₁₃, П₁₇) (П₈ > П₆ > П₁₄) (74)

При последовательном выделении множеств эффективных решений коэффициент определенности выбора составлял для первого подмножества, включавшего П₁, П₃, П₅, П₁₀, П₁₆ величину, равную

.

Для второго подмножества этот коэффициент равен

.

Для третьего подмножества имеем

.

Для четвертого подмножества коэффициент равен

.

Для пятого и шестого подмножества этот коэффициент также равен единице, поскольку множества эффективных радений на этих этапах включали только по одному предприятию. Упорядочение (74) дало разбиение всех предприятий по группам.

В рамках располагаемой информации дальнейшее уточнение мест, занимаемых предприятиями внутри групп, невозможно. Если использовать дополнительную информацию, об относительной важности показателей, то можно получить дальнейшее уточнение ранжирования предприятий. С практической точки зрения, например, важно определить какое предприятие является наилучшим. Методы определения единственного наилучшего решения рассматриваются в следующем параграфе.

Таблица 28

Показатели	А	Б	В	Г	Д
Предприятия	рубли	ранги	%	ранги	руб./ руб.	ранги	руб./ руб.	ранги	руб./ руб.	ранги
П1 П2 П3 П4 П5 П6 П7 П8 П9 П10 П11 П12 П13 П14 П15 П16 П17

На таблице 23: А - Производительность труда (выработка одного работающего);

Б - Рентабельность по себестоимости (прибыль / затраты);

В - Рентабельность по фондам (прибыль / ср. стоимость основных фондов);

Г - Себестоимость (затраты на один рубль доходов);

Д - Фондоотдача.

Дата добавления: 2014-01-07