Определение единственного решения

Определение единственного правильного решения является заключительным этапом процедуры выбора. В соответствии со свойствами множества эффективных решений, изложенных в предыдущем параграфе, единственное решение должно выбираться именно из этого множества. Любое выбранное решение из множества эффективных решений является недоминируемым, т.е. оно не хуже любого другого решения. В связи с этим, если нет возможности получить дополнительную информацию вследствие затрат времени и ресурсов, выбор любого решения из множества эффективных решений обеспечивает гарантированный результат, что это решение не хуже, чем любое другое решение. Этот вывод, полученный в теории принятия решений, дает основание ЛПР в условиях отсутствия новой информации волевым порядком выбирать любое решение из множества эффективных решений. Обоснованием для этого выбора является утверждение, что это решение не хуже других.

Определение единственного оптимального решения из множества эффективных решений, требует привлечения дополнительной информации. Действительно, вся исходная информация полностью использована для выделения мно­жества эффективных решений из допустимого множества. В качестве дополнительной информации целесообразно использовать:

1. Непосредственную ранжировку эффективности решений;

2. Уточнение предпочтения решений экспертами;

3. Информацию о свойствах функции группового предпочтения.

Проведение непосредственной ранжировки множества эффективных решений является наиболее простым способом определения оптимального решения. Однако ранжировка практически возможна, если имеется уверенность в том, что эксперты обладают необходимой компетентностью в различении эффективных решений и, кроме того, если количество эффективных решений невелико (10-15). При невыполнении перечисленных условий проведение ранжировки практически даст тот же эффект, что и выбор произвольного решения из множества эффективных. Другими словами эта ранжировка позволяет определить единственное решение, в отношении которого можно гарантировать только то, что оно не хуже любого другого.

Уточнение предпочтения решений экспертами преследует цель возможного сужения области эффективных решений. Для этого необходимо провести анализ: какие предпочтения привели к образованию множества эффективных решений; какое из эффективных решений по расположению среди других решений является наиболее подходящим кандидатом на наилучшее решение; какие решения являются наиболее вероятными для исключения и т.п. Такой анализ требует тщательного изучения структуры, взаимного положения решений как точек в пространстве предпочтений члена группового ЛПР или при векторной оптимизации в пространстве показателей (характеристик) решений. Результаты исследования множества эффективных решений позволяют целенаправленно сформулировать задачи для уточнения, предпочтения решений. Практически уточнение предпочтения решений приводит лишь к некоторому сужению множества эффективных решений. Ожидать получение единственного оптимального решения на основе уточнения предпочтений маловероятно.

Информация о свойствах функции группового предпочтения может включать свойства выпуклости, линейности или другие характерные особенности, отражавшие зависимость от индивидуальных предпочтений. Получение такой информации требует определения той или иной формы компромисса между членами группового ЛПР или между компонентами вектора характеристик решений в случае векторной оптимизации. Наиболее эффективным, о точки зрения отыскания оптимального решения, является предположение о линейности функции группового предпочтения. Как и в §8 будем использовать коэффициенты решений a_is, где i – номер решения, s – номер члена группового ЛПР (в случае векторной оптимизации s – номер показателя качества решения). Используя коэффициенты решений, представим линейную функцию группового предпочтения в виде

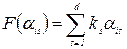(75)

где k_s – коэффициенты весов членов группового ЛПР (в случае векторной оптимизации k_s – коэффициенты весов показателей); d – количество членов в групповом ЛПР (количество показателей).

При изменении предпочтения решений в количественных шкалах коэффициенты весов равны

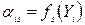(76)

поэтому линейная функция группового предпочтения может быть записана в виде

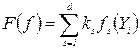(77)

При измерении предпочтения решений в порядковой шкале коэффициент весов определяется формулами (50), (51), (52).

Если коэффициенты весов k_s известны, то определение оптимального решения производится максимализацией суммы (1) по всем эффективным решениям

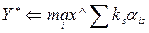(78)

Номер i есть номер решения: именно по этому индексу выполняется максимум.

Если коэффициенты весов k_s неизвестны, то их определение может быт выполнено различными способами. При уверенности и достаточной точности коэффициенты можно определить экспертным путем.

Другие способы определения коэффициентов решений основаны на различных предположениях о компетентности («весе») членов группового ЛПР или важности показателей в случае векторной оптимизации.

Дата добавления: 2014-01-07