Описание случайных погрешностей с помощью функций распределения

Эмпирически были установлены следующие правила округления рассчитанного значения погрешности и полученного результата измерения.

Правила округления результатов измерений

Поскольку погрешности измерений определяют лишь зону неопределенности результатов, их не требуется знать очень точно. В окончательной записи погрешность измерения принято выражать числом с одним или двумя значащими цифрами.

1. Погрешность результата измерения указывается двумя значащими цифрами, если первая из них равна 1 или 2, и одной – если первая цифра равна 3 или более.

2. Результат измерения округляется до того нее десятичного знака, которым оканчивается округленное значение абсолютной погрешности. Если десятичная дробь в числовом значении результата измерений оканчивается нулями, то нули отбрасываются до того разряда, который соответствует разряду числового значения погрешности.

3. Если цифра старшего из отбрасываемых разрядов меньше 5, то остальные цифры числа не изменяются. Лишние цифры в целых числах заменяются нулями, а в десятичных дробях отбрасываются.

4. Если цифра старшего из отбрасываемых разрядов больше или равна 5, но за ней следуют отличные от нуля цифры, то последнюю оставляемую цифру увеличивают на единицу.

5. Если отбрасываемая цифра равна 5, а следующие за ней цифры неизвестны или нули, то последнюю сохраняемую цифру числа не изменяют, если она четная, и увеличивают на единицу, если она нечетная.

6. Округление производится лишь в окончательном ответе, а все предварительные вычисления проводят с одним-двумя лишними знаками.

Результат измерения, и его погрешность могут рассматриваться как случайные величины. Случайные величины могут быть описаны функциями распределения: интегральной и дифференциальной.

Под интегральной функцией распределения результатов наблюдений понимается зависимость вероятности того, что результат наблюдений Х i в i -м опыте окажется меньшим некоторого текущего значения х от самой величины Хi

где Р – символ вероятности события, указанного в фигурных скобках.

График интегральной функции распределения (рис. 5.1).

Значение интегральной функции в точке Х численно равно вероятности того, что случайная величина Xi в результате i -гo наблюдения окажется левее точки X. При перемещении точки Х вдоль оси ОХ эта вероятность будет, очевидно, изменяться, но она не может уменьшиться при перемещении точки Х вправо. Поэтому интегральная функция распределения является неубывающей функцией аргумента. Значение интегральной функции распределения в общем случае при перемещении точки Х из «–» в «+» изменяется от 0 до 1. Теоретическая интегральная функция непрерывна, т.е. результат наблюдения может принять любое заранее выбранное значение с нулевой вероятностью.

Рис. 5.1. График интегральной функции распределения:

а);

б);

в)

Более наглядным является описание свойств результатов измерений и случайных погрешностей с помощью дифференциальной функции распределения, иначе называемой плотностью распределения вероятностей р (х) = dF (x)/ dx. Она всегда неотрицательна и подчиняется условию нормирования в виде:

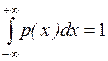
Учитывая взаимосвязь F (x) и р (х), легко показать, что вероятность попадания случайной величины в заданный интервал (х 1; х 2)

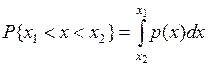
Из последнего уравнения следует, что вероятность попадания случайной величины х в заданный интервал (х 1; х 2) равна площади, заключенной под кривой р (х) между абсциссами х 1 и х 2 (см. рис.5.2). Поэтому по форме кривой плотности вероятности р (х) можно судить о том, какие значения случайной величины х наиболее вероятны, а какие наименее.

Рис. 5.2. ***

а)

б)

В практике измерений встречаются различные формы кривой закона распределения, однако чаще всего имеют дело с нормальным и равномерным распределением плотности вероятностей.

Нормальное распределение плотности вероятности (рис.5.3) характерно тем, что, согласно центральной предельной теореме теории вероятностей, такое распределение имеет сумма бесконечно большого числа бесконечно малых случайных возмущений с любыми распределениями. Применительно к измерениям это означает, что нормальное распределение случайных погрешностей возникает тогда, когда на результат измерения действует множество случайных возмущений, ни одно из которых не является преобладающим. Практически, суммарное воздействие даже сравнительно небольшого числа возмущений приводит к закону распределения результатов и погрешностей измерений, близкому к нормальному.

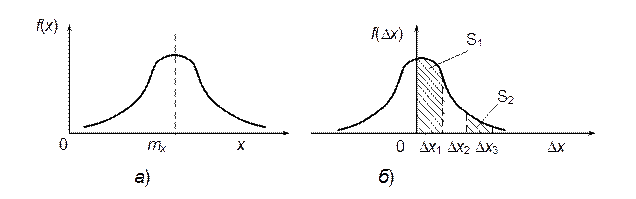
Рис. 5.3. Нормальное распределение плотности вероятности:

а)

б)

В аналитической форме нормальный закон распределения выражается формулой

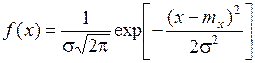
где х – случайная величина;

m_х – математическое ожидание случайной величины;

σ – среднее квадратическое отклонение.

Перенеся начало координат в центр распределения m_х и откладывая по оси абсцисс погрешность Δ х = х – m_х, получим кривую нормального распределения погрешностей:

.

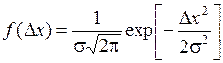Для группы из и наблюдений, распределенных по нормальному закону:

;

.

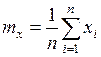Нормальное распределение погрешностей имеет некоторые свойства:

• Кривая нормального распределения погрешностей симметрична относительно оси ординат. Это означает, что погрешности, одинаковые по величине, но противоположные по знаку, имеют одинаковую плотность вероятностей, т.е. при большом числе наблюдений встречаются одинаково часто. Математическое ожидание случайной погрешности равно нулю.

• Из характера кривой следует, что при нормальном законе распределения малые погрешности будут встречаться чаще, чем большие. Так, вероятность появления погрешностей, укладывающихся в интервал от 0 до Δ х 1 характеризуемая площадью S 1, (см. рис. 5.3) будет значительно больше, чем вероятность появления погрешностей в интервале от Δ х 2 до Δ х 2 (площадь S 1).

На рис. 5.4 изображены кривые нормального распределения с различными средними квадратическими отклонениями, причем σ 1 > σ 2 > σ 3.

Сравнивая кривые между собой можно убедиться, что чем меньше СКО, тем меньше рассеяние результатов наблюдений и тем больше вероятность того, что большинство случайных погрешностей в них будет мало. Естественно заключить, что качество измерений тем выше, чем меньше СКО случайных погрешностей.

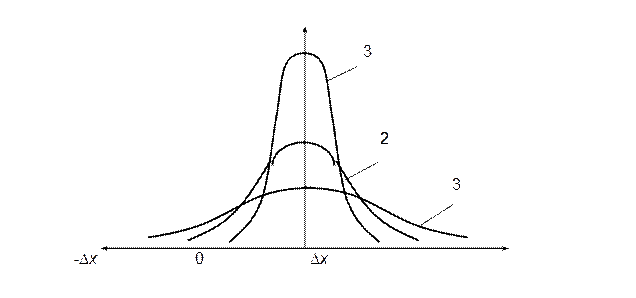Рис. 5.4. Кривые нормального распределения с различными средними

квадратическими отклонениями

Дата добавления: 2014-01-07