Аналитическая запись функций алгебры логики

Выше было показано, что всякая формула реализует некоторую истинностную функцию. Эквивалентные формулы реализуют одну и ту же функцию. Т.е. по формуле всегда можно найти соответствующую ей функцию. Теперь рассмотрим вопрос о том, как записать функцию алгебры логики в виде формулы, т.е. рассмотрим в некотором смысле обратную задачу.

Для этого введем параметризацию, позволяющую охарактеризовать значение переменной в «энке». Обозначим 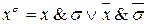, где параметр s равен нулю или единице. Таким образом, 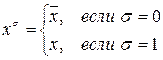. Т.е. если на наборе значение переменной х равно 0, то будем писать «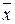», а в случае, когда соответствующее значение равно 1, то будем записывать просто «х». Заметим, что х^s =1 тогда и только тогда, когда х = s.

Теорема 1.10.1. О разложении функции по переменным.

Каждую истинностную функцию от n аргументов f (x ₁, x ₂,…, x_n) при любом m (1 £ m £ n) можно представить формулой вида:
(1) 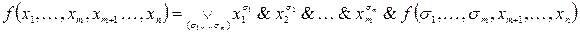, где дизъюнкция берется по всевозможным наборам значений переменных х ₁,…, х_m.

Представление функции в виде (1) называется разложением функции по m переменным х ₁,…, х_m.

Доказательство:

Рассмотрим произвольный набор значений переменных (a ₁, a ₂,…, a_n). Покажем, что левая и правая части (1) имеют на этом наборе одинаковые значения. Значение левой части равно f (a ₁, a ₂,…, a_n). Вычислим значение правой части: . Ненулевые члены в дизъюнкции получаются только в том случае, когда набор s ₁, s ₂,…, s_m совпадает с набором a ₁, a ₂,…, a_m, т.е. в последнем выражении остается только одно ненулевое слагаемое: . И т.к. , то это слагаемое равно f (a ₁, a ₂,…, a_n). Таким образом, значения левой и правой части (1) совпадают на произвольном наборе (a ₁, a ₂,…, a_n).

Следствия:

1) О разложении по одной переменной.

Если в выражении (1) m =1, то
f (х ₁, х ₂,…, х_n) = x_n & f (х ₁, х ₂,…, 1)Ú & f (х ₁, х ₂,…, 0);

2) О разложении по всем n переменным или совершенные дизъюнктивные нормальные формы (СДНФ).

Если в выражении (1) m = n, то . Если f (х ₁, х ₂,…, х_n) не равна тождественно нулю, то в последнюю дизъюнкцию будут давать вклад только те компоненты, где f (s ₁, s ₂,…, s_n)=1, поэтому
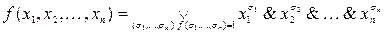. Это разложение называется совершенной дизъюнктивной нормальной формой (СДНФ). И, как следует из её определения, для построения СДНФ в таблице истинности функции f надо рассматривать лишь те строки, где функция равна единице. Для каждой такой строки записывается элементарная конъюнкция, состоящая из всех переменных функции. При этом переменная входит в конъюнкцию с отрицанием, если в рассматриваемой строке её значение равно нулю, и без отрицания – в противном случае.

3) Совершенные конъюнктивные нормальные формы (СКНФ).

Совершенная дизъюнктивная нормальная форма есть выражение вида 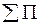– сумма произведений. Используя принцип двойственности для построения эквивалентных формул, можно получить разложение вида – произведение сумм, которое носит название совершенной конъюнктивной нормальной формы. Так как , то для

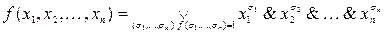
, но 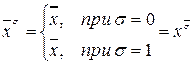. Поэтому . Заметим, что при построении последней формулы участвуют лишь такие наборы s ₁, s ₂,…, s_n, на которых f (s ₁, s ₂,…, s_n)=1. Тогда в построении формулы для будут участвовать наборы s ₁, s ₂,…, s_n, где , или f (s ₁,…, s_n)=0.

Таким образом, если f (х ₁,…, х_n) ¹ 1, то
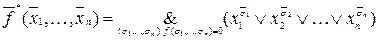– это и есть СКНФ. И, как следует из её определения, для построения СКНФ в таблице истинности функции f надо рассматривать лишь те строки, где функция равна нулю. Для каждой такой строки записывается элементарная дизъюнкция, состоящая из всех переменных функции. При этом переменная входит в дизъюнкцию с отрицанием, если в рассматриваемой строке её значение равно единице, и без отрицания – в противном случае.

Примеры построения СДНФ и СКНФ.

Таблица 14

x	у	f (x, у)	СДНФ	СКНФ
			x & y

В таблице 14 в столбце СДНФ показаны элементарные конъюнкции в единичных строках функции, а в столбце СКНФ – элементарная дизъюнкция в строке, где функция равна нулю. Тем самым, СДНФ= Ú Ú x & y, СКНФ =. Эти формулы эквивалентны между собой и эквивалентны формуле (х ® у).

Таблица 15

x	у	f (x, у)	СДНФ	СКНФ
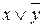
			x & y

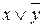В таблице 15 в столбце СДНФ показаны элементарные конъюнкции в единичных строках функции, а в столбце СКНФ – элементарные дизъюнкции в нулевых строках. Тем самым, СДНФ= Ú x & y, СКНФ =()&(). Эти формулы эквивалентны между собой и эквивалентны формуле (х º у).

Таким образом, построение СДНФ и СКНФ – это ещё одна возможность записать тождество.

Дата добавления: 2014-01-07