Теорема о тройке связок

Теорема 1.12.1. Всякая истинностная функция может быть выражена формулой, содержащей только связки {Ø, &, Ú}.

Доказательство:

Рассмотрим два случая:
(1) если f (х ₁, х ₂,…, х_n)º0 – противоречие или f (х ₁, х ₂,…, х_n)º1 – тавтология, тогда очевидно, f (х ₁, х ₂,…, х_n)=или f (х ₁, х ₂,…, х_n)=,
(2) если f (х ₁, х ₂,…, х_n)¹0 (и ¹1). Тогда представим её в виде СДНФ или СКНФ. В полученной формуле имеются только связки из множества {Ø, &, Ú}.

Следствие 1: о парах связок.

Для любой из следующих пар связок {Ø,&}, {Ø,Ú} и {Ø,®} и для любой функции алгебры логики можно построить формулу, реализующую эту функцию и содержащую связки только из заданной пары.

Доказательство:

Пусть для функции построена совершенная дизъюнктивная (или конъюнктивная) нормальная форма, т.е. формула, содержащая только связки {Ø,&,Ú}. Заметим, что выражение является тождеством. Поэтому все выражения вида х Ú у можно заменить эквивалентными 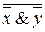и содержащими только связки {Ø,&}. Тем самым, полученная в результате проведенных преобразований формула содержит только связки из заданной пары.

Для представления функции формулой со связками {Ø,Ú} аналогичным образом можно воспользоваться тождеством 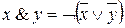. И, выполнив замены всех подформул вида х & у на эквивалентную формулу , получить в результате формулу со связками из заданной пары.

Для перехода в формуле к последней паре связок {Ø,®} можно воспользоваться тождествами: и

Следствие 2: об уникальных связках.

Любая истинностная функция может быть выражена формулой с использованием лишь одной связки стрелки Пирса – {¯}или штриха Шеффера – {½}.

Доказательство:

Таблица 16

x	у	x ¯ у	x ½ у

Из таблицы 16 следует: СДНФ(x ¯ у)=

СКНФ(x ½ у)=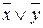

Нетрудно также проверить, что имеют место следующие тождества: 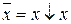и .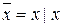

Тем самым, х & y =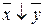 = (x ¯ x) ¯ (у ¯ у) и х Ú y = 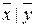= (x ½ x) ½ (у ½ у). Последние тождества можно использовать для перехода в формуле от связок {Ø,&,Ú} к стрелке Пирса или к штриху Шеффера.

Вообще говоря, связки ¯ и ½ являются единственными элементарными функциями, каждой из которых достаточно для записи формул всех других истинностных функций.

Рассмотрим применение следствий 1 и 2 на примере.

Запишем формулу х ® у с использованием только связок {Ø,&}: х ® у =. С использованием связок {Ø,Ú}: х ® у =. С использованием только {¯}: х ® у = ((х ¯ х) ¯ у) ¯ ((х ¯ х) ¯ у). И, наконец, с использованием только {½}: х ® у = (x ½ (у ½ у)).

Дата добавления: 2014-01-07