Теорема Поста о полноте

Следующая теорема является необходимым и достаточным условием полноты системы функций алгебры логики.

Теорема 1.16.1. О полноте.

Система функций алгебры логики является полной тогда, и только тогда, когда она целиком не содержится ни в одном из пяти замкнутых классов: Т₀, Т₁, S, M и L. Иными словами среди функций этой системы обязательно имеются функции, не сохраняющие ноль и единицу, а также несамодвойственная, немонотонная и нелинейная функции.

Доказательство:

1) Необходимость: итак, система функций F полна. Покажем, что она не содержится целиком ни в одном из пяти замкнутых классов. Предположим обратное: F полная система и содержится в каком-нибудь из замкнутых классов. Обозначим этот класс Х. Таким образом, по предположению F Í Х. Тогда по свойствам замыканий [ F ]Í [ Х ]. Но Х – замкнутый класс, поэтому [ Х ]= Х. А F – полная система и [ F ]= Р ₂. Тем самым, Р ₂Í Х, что невозможно. Полученное противоречие опровергает сделанное предположение, поэтому F не содержится целиком ни в одном из пяти замкнутых классов.

2) Достаточность: итак, система функций F не содержится целиком ни в одном из пяти замкнутых классов. Покажем, что она является функционально полной системой функций. Поскольку F не содержится целиком ни в одном из классов Т₀, Т₁, S, M и L, то среди функций этой системы обязательно имеются функции, не сохраняющие ноль и единицу, а также несамодвойственная, немонотонная и нелинейная функции. Обозначим эти функции f ₀, f ₁, f_S, f_M и f_L соответственно. Рассмотрим систему функций F ¢={ f ₀, f ₁, f_S, f_M, f_L }. Понятно, что система F ¢ является подсистемой системы F, т.е. F ¢Í F, и если будет доказано, что F ¢ полна, то тоже самое можно будет сказать и о системе F. Можно считать, что все функции системы F ¢={ f ₀, f ₁, f_S, f_M, f_L } зависят от одних и тех же переменных х ₁, х ₂,…, х_n. Покажем, что функции полной системы {Ø,&} могут быть выражены формулой через функции системы F ¢.

Рассмотрим f ₀ÏТ₀, для этой функции возможны два случая: 1) f ₀(1,1,…,1)=1 и 2) f ₀(1,1,…,1)=0 (заметим также, что f ₀(0,0,…,0)=1).

Разберем случай 1): т.к. f ₀(1,1,…,1)=1 и f ₀(0,0,…,0)=1, то выполнив замену всех переменных этой функции на х, получим функцию от одной переменной j (х)= f ₀(х, х,…, х)=1 при любых х, т.е. получили константу 1. Аналогичным способом с помощью функции f ₁ можно получить константу 0. Теперь с помощью немонотонной функции f_M и констант 0 и 1 по лемме о немонотонной функции можно получить функцию 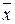. И далее по лемме о нелинейной функции с помощью констант 0, 1 и функций 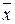и f_L получим &. Таким образом, любая из функций системы {Ø,&} выражается формулой через функции f ₀, f ₁, f_M, f_L системы F ¢. И так как система {Ø,&} является полной, то по теореме о полных системах функций система F ¢ также полна.

Теперь разберем случай 2): т.к. f ₀(1,1,…,1)=0 и f ₀(0,0,…,0)=1, то выполнив замену всех переменных функции f ₀ на х, получим функцию от одной переменной j (х)= f ₀(х, х,…, х)= 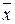(j (0)=1, j (1)=0). Теперь из функций х, 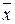и f_S по лемме о несамодвойственной функции получим константы 0 и 1. И далее так же, как и в первом случае из функций 0, 1, 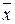и f_L получим &. Тем самым, любая из функций системы {Ø,&} выражается формулой через функции f ₀, f ₁, f_S, f_L системы F ¢. Следовательно, F ¢ полная система. И теорема доказана.

Следствие 1: из всякой полной в Р ₂ системы функций можно выделить полную подсистему, содержащую не более четырех функций.

Действительно, при доказательстве первого случая в теореме использовались только функции f ₀, f ₁, f_М, f_L, а второго – функции f ₀, f ₁, f_S, f_L.

Следствие 2: всякий замкнутый класс функций алгебры логики, не совпадающий с множеством всех функций алгебры логики, содержится по крайней мере в одном из классов Т₀, Т₁, S, M или L.

В этом смысле классы Т₀, Т₁, S, M и L являются максимальными или предполными, поскольку добавление к любому из них любой истинностной функции, не принадлежащей классу, приводит к полной системе функций.

Следствие 3: в алгебре логики существует только пять предполных классов: Т₀, Т₁, S, M и L.

Полная система функций алгебры логики называется базисом в Р ₂, если никакая её собственная подсистема не является полной. Иными словами базис – это минимальная по числу функций полная система. Важно, что любая из функций алгебры логики записывается формулой через функции базиса.

Используя теорему о полноте, несложно установить, является ли полной заданная система функций и образует ли она базис? Рассмотрим решение этого вопроса на примере.

Пусть имеется система функций: {0, 1, ®, Å, Ø}. Очевидно, что эта система является функционально полной, поскольку полна её собственная подсистема {Ø, ®}. Понятно также, что исходная система функций не является базисом, т.к. из неё можно удалить функции 0, 1 и Å, и оставшиеся функции все ещё составляют полную систему. Выясним теперь, имеются ли в заданной системе другие полные подсистемы, образующие базис. Для этого составим таблицу принадлежности функций {0, 1, ®, Å, Ø} пяти замкнутым классам.

Таблица 18

	Т0	Т1	S	M	L
	+	–	–	+	+
	–	+	–	+	+
®	–	+	–	–	–
Å	+	–	–	–	+
	–	–	+	–	+

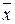
Из таблицы 18 видно, что базисами являются следующие множества функций: {Ø, ®}, {0, ®}, {Å,® }. Других базисов в данной системе нет.

Глава 2. Минимизация булевых функций

Дата добавления: 2014-01-07