Замыкание систем функций алгебры логики

Рассмотрим ещё два понятия: замыкания и замкнутого класса, которые тесно связаны с понятием полноты.

Пусть М Í Р ₂ – некоторое подмножество множества всех функций алгебры логики. Замыканием М называется множество тех истинностных функций, которые могут быть выражены формулой над М.

Замыкание М обозначается [ M ].

Примеры:

1) Пусть М = Р ₂, тогда [ M ] = Р ₂.

2) Пусть М = {¯}, тогда [ M ] = Р ₂.

3) Пусть М = {1,Å}, тогда [ M ] = { f (x ₁,…, x_n)Î P ₂: f (x ₁,…, x_n) = c ₀Å c ₁ x ₁żŠc_nx_n, где с_i =0 или 1}. Т.е. [ M ] – это множество функций, представимых линейным выражением или класс всех линейных функций.

Свойства замыкания:

1) Для всякого множества функций алгебры логики М замыкание «шире» самого множества М. Или [ M ] Ê М.

2) Для всякого множества функций М замыкание замыкания М есть само замыкание М. Или [[ M ]] = [ М ].

3) Если множество функций М ₁ является подмножеством множества функций М ₂, то замыкание М ₁ является подмножеством замыкания М ₂. Или если М ₁ Í М ₂, то [ М ₁] Í [ М ₂].

4) Объединение замыканий двух множеств является подмножеством замыкания объединения этих множеств. Или [ М ₁] È [ М ₂] Í [ М ₁ È М ₂].

Класс функций М называется функционально замкнутым или просто замкнутым, если его замыкание совпадает с ним самим, т.е. [ M ] = М.

Так, например, множество всех функций алгебры логики – функционально замкнутый класс. А множества {Ø,&}, {Ø,Ú}, {Ø,®} не являются замкнутыми классами, поскольку их замыканием является множество всех функций алгебры логики. То же можно сказать и о других полных системах функций. Тем самым, определение полной системы функций можно сформулировать в терминах замыканий: система функций М является функционально полной, если её замыкание совпадает с множеством всех функций алгебры логики, т.е. [ M ]= P ₂.

§ 1.15. Важнейшие замкнутые классы

1) Класс функций, сохраняющих ноль. Обозначение: Т₀.

Т₀={ f (x ₁, x ₂,…, x_n)Î P ₂: f (0,0,…,0)=0}, таким образом, этот класс состоит из тех функций алгебры логики, которые на наборе, состоящем из одних нулей, имеют значение ноль. Или, что то же самое, в верхней строке таблицы истинности значение этих функций равно нулю. И поскольку, ровно половина всех функций в верхней строке равны нулю, то число функций от n переменных, относящихся к классу Т₀, равно . Из элементарных функций к этому классу относятся следующие: 0, х, &, Ú, Å. А такие, как 1, 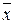, º, ® не принадлежат классу Т₀.

Утверждение:

Т₀ – замкнутый класс, т.е. [Т₀]=T₀.

Доказательство:

По свойствам замыканий Т₀ Í [Т₀]. Покажем, что [Т₀] Í Т₀. Для этого рассмотрим произвольную функцию ФÎ [Т₀]. По определению замыкания функция Ф выражается формулой через функции класса Т₀, т.е. Ф= f (f ₁, f ₂,…, f_m), где функции f, f ₁, f ₂,…, f_m ÎТ₀. Тогда Ф(0,0,…,0)= f (f ₁(0,…,0), f ₂(0,…,0),…, f_m (0,…,0)) = f (0,…,0)=0. Таким образом, функция ФÎТ₀. И так как Ф – произвольная функция из замыкания, то [Т₀] Í Т₀. И, следовательно, [Т₀] = Т₀.

2) Класс функций, сохраняющих единицу. Обозначение: Т₁.

Т₁={ f (x ₁, x ₂,…, x_n)Î P ₂: f (1,1,…,1)=1}, таким образом, этот класс состоит из тех функций алгебры логики, которые на наборе, состоящем из одних единиц, имеют значение 1. Или, что то же самое, в нижней строке таблицы истинности значение этих функций равно единице. И, поскольку, ровно половина всех функций в нижней строке равны единице, то число функций от n переменных, относящихся к классу Т₁, равно . Из элементарных функций к этому классу относятся следующие: 1, х, &, Ú, º, ®. А такие, как 0, 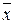, Å не принадлежат классу Т₁.

Утверждение:

Т₁ – замкнутый класс, т.е. [Т₁]=T₁.

Доказательство:

По свойствам замыканий Т₁ Í [Т₁]. Покажем, что [Т₁] Í Т₁. Для этого рассмотрим произвольную функцию ФÎ [Т₁]. По определению замыкания функция Ф выражается формулой через функции класса Т₁, т.е. Ф= f (f ₁, f ₂,…, f_m), где функции f, f ₁, f ₂,…, f_m ÎТ₁. Тогда Ф(1,1,…,1)= f (f ₁(1,…,1), f ₂(1,…,1),…, f_m (1,…,1)) = f (1,…,1)=1. Таким образом, произвольно взятая функция Ф из [Т₁] принадлежит и классу Т₁. Поэтому [Т₀] Í Т₀. Следовательно [Т₀] = Т₀.

3) Класс самодвойственных функций. Обозначение: S.

S ={ f (x ₁, x ₂,…, x_n)Î P ₂: f (x ₁, x ₂,…, x_n)= f ^*(x ₁, x ₂,…, x_n) }, таким образом, этот класс состоит из тех функций алгебры логики, которые совпадают с двойственными к ним. Заметим, что такие функции на противоположных наборах принимают противоположные значения, т.к. f (x ₁, x ₂,…, x_n)=. Таблицы истинности этих функций имеют зеркальную симметрию верхней половины строк таблицы и инвертированной нижней половины строк относительно середины всех строк таблицы. Тем самым, самодвойственные функции полностью определяются своими значениями на первой половине строк таблицы. Число таких строк для функций от n переменных равно =2 ^{n -1} и, следовательно, число функций от n переменных, относящихся к классу S, равно . Из элементарных функций самодвойственными являются только тождественная функция х и отрицание .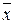

Утверждение:

S – замкнутый класс, т.е. [ S ]= S.

Доказательство:

По свойствам замыканий S Í [ S ]. Покажем, что [ S ] Í S. Для этого рассмотрим произвольную функцию ФÎ[ S ]. По определению замыкания функция Ф выражается формулой через функции класса S, т.е. Ф= f (f ₁, f ₂,…, f_m), где функции f, f ₁, f ₂,…, f_m Î S. Тогда Ф^*= f ^*(f ₁^*, f ₂^*,…, f_m ^*) = f (f ₁, f ₂,…, f_m)=Ф. Таким образом, функция ФÎ S. И так как Ф – произвольная функция из замыкания, то [ S ] Í S. Отсюда следует, что [ S ] = S.

Лемма о несамодвойственной функции.

Если функция алгебры логики не принадлежит классу самодвойственных функций, то всегда можно указать такую замену её переменных функциями х и 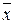, что в результате этой замены будет получена константа 0 или 1.

Доказательство:

Доказательство имеет конструктивный характер и показывает, как подобрать такую замену переменных. Рассмотрим произвольную несамодвойственную функцию от n переменных f (x ₁, x ₂,…, x_n). Так как f S, то существует такой набор значений переменных a ₁, a ₂,…, a_n, что f (a ₁, a ₂,…, a_n), а это значит, что f (a ₁, a ₂,…, a_n) =. Заметим, что для самодвойственной функции такого набора не существует по определению. Введем также в рассмотрение функции g_i (x)= x^ai, где i =1,2,…, n, и g_i (x) равно либо х, либо 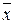, в зависимости от значения a_i. Произведем замену переменных x ₁, x ₂,…, x_n в функции f на g ₁(x), g ₂(x),…, g_n (x) соответственно. Покажем, что полученная в результате этой замены функция Ф(х)= f (g ₁(x), g ₂(x),…, g_n (x)) является константой. Действительно, т.к. Ф(х)= f (x^{a 1}, x^{a 2},…, x^an), то Ф(0)= f (0 ^{a 1},0 ^{a 2},…,0 ^an), но 0 ^ai равно =1, если a_i =0, и равно 0, если a_i =1, тем самым, 0 ^ai =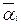. Тогда Ф(0)==^{(по условию)} f (a ₁, a ₂,…, a_n) = f (1 ^{a 1},1 ^{a 2},…,1 ^an) = Ф(1). Т.е. Ф(х) имеет постоянное значение для всех значений х, и Ф(х) – константа.

Пусть функция f (х, y, z)=. Заметим, что f (0,0,0)= f (1,1,1). Поэтому набор (1,1,1) можно взять для формирования функций g_i (x)= x^ai, где i =1,2,3. На выбранном наборе все эти функции равны тождественной функции х. Выполним замену каждой переменной на х. Получим: f (х, х, х)= .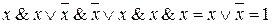

Понятно, что никакая замена переменных на х или 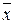в самодвойственной функции не может привести к константе, а только к х или .

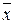4) Класс монотонных функций. Обозначение: М.

Функция f (x ₁, x ₂,…, x_n)Î P ₂ называется монотонной, если для любых двух наборов a =(a ₁, a ₂,…, a_n) и b =(b ₁, b ₂,…, b_n) таких, что a_i £ b_i, где i =1,2,…, n, следует f (a) £ f (b). Про такие наборы говорят, что набор a предшествует набору b, и обозначают a £ b. Из элементарных функций монотонными являются 0, 1, тождественная функция х, &, Ú. А функции 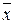, ®, ½, ¯, Å, º монотонными не являются.

Утверждение:

М – замкнутый класс, т.е. [ М ]= М.

Доказательство:

По свойствам замыканий М Í [ М ]. Покажем, что [ М ] Í М. Т.к. функция х Î М, то достаточно рассмотреть произвольную функцию ФÎ[ М ]. По определению замыкания функция Ф выражается формулой через функции класса М, т.е. Ф(x ₁, x ₂,…, x_n)= f (f ₁, f ₂,…, f_m), где функции f, f ₁, f ₂,…, f_m Î М. Пусть a =(a ₁, a ₂,…, a_n) и b =(b ₁, b ₂,…, b_n) – два набора значений переменных (x ₁, x ₂,…, x_n) таких, что a_i £ b_i, где i =1,2,…, n. Эти наборы определяют наборы значений переменных для функций f ₁, f ₂,…, f_m: а ₁=(a ₁₁, a ₁₂,…, a _{1 s 1}) и b ₁=(b ₁₁, b ₁₂,…, b _{1 s 1}),…, а_m =(a_{m 1}, a_{m 2},…, a_msm) и b_m =(b_{m 1}, b_{m 2},…, b_msm), которые (вследствие того, что a £ b) также попарно предшествуют друг другу. Т.е. а ₁ £ b ₁ и а ₂ £ b ₂ и … а_m £ b_m. Но функции f ₁, f ₂,…, f_m монотонны, поэтому f ₁(а ₁) £ f ₁(b ₁), f ₂(а ₂) £ f ₂(b ₂), …, f_m (а_m) £ f_m (b_m). Тогда рассматривая a ¢=(f ₁(а ₁), f ₂(а ₂),…, f_m (а_m)) и b ¢=(f ₁(b ₁), f ₂(b ₂), …, f_m (b_m)) как наборы значений переменных функции f, имеем: a ¢ £ b ¢ и f (a ¢) £ f (b ¢) ввиду монотонности f. Но Ф(a)= f (a ¢) и Ф(b)= f (b ¢), т.е. для a £ b Þ Ф(a) £ Ф(b). И, следовательно, функция ФÎ М. Но Ф – произвольная функция из замыкания, поэтому [ М ] Í М. Отсюда по определению равных множеств следует: [ М ] = М.

Лемма о немонотонной функции.

Если функция алгебры логики не принадлежит классу монотонных функций, то из неё путем подстановки констант 0, 1 и функции х на места переменных можно получить функцию .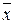

Доказательство:

Доказательство имеет конструктивный характер и показывает, как подобрать такую замену переменных. Рассмотрим произвольную немонотонную функцию от n переменных f (x ₁, x ₂,…, x_n). Так как f М, то существуют такие наборы значений переменных a и b, что a £ b и f (a) > f (b).

Если наборы a и b смежны, т.е. различаются только одной i –той координатой (при этом в наборе a на i –том месте стоит ноль, а в наборе b – единица), то цель достигнута – можно сделать замену переменных (x ₁, x ₂,…, x_n) на (a ₁,…, a_i‑1, x, a_i+1,…, a_n). После этой замены будет получена функция одной переменной g (x)= f (a ₁,…, a_i‑1, x, a_i+1,…, a_n). Причем g (0)= f (a ₁,…, a_i‑1,0, a_i+1,…, a_n) = f (a), а g (1)= f (a ₁,…, a_i‑1,1, a_i+1,…, a_n)= f (b). И так как f (a) > f (b), то g (0) > g (1), а это значит, что g (0)=1 и g (1)=0, т.е. g (x)=.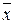

Если же наборы a и b несмежны, то они отличаются в нескольких координатах, и пусть число этих координат равно k (где k >1). И так как a £ b, то в наборе a эти k координат равны 0, а в наборе b они равны 1. Поэтому между наборами a и b можно вставить (k ‑1) промежуточных наборов g ₁, g ₂,…,g _k-1 таких, что a £ g ₁ £ g ₂ £…£ g _k-1 £ b, образующих цепь смежных наборов, связывающих a и b. И так как f (a) > f (b), то в этой цепи существуют два смежных набора g _i и g _i+1 (где g _i £ g _i+1), для которых f (g _i) > f (g _i+1). Тогда также, как и в первом случае, эти наборы g _i и g _i+1 можно использовать для замены.

Пусть функция f (х, y)= х ® у. Заметим, что на наборах (0,0) и (1,0), которые являются смежными, значения функции находятся в соотношении: f (0,0)> f (1,0). Поэтому можно выполнить замену переменной у на 0, а переменную х оставить без изменений. После замены получим: f (х,0)= х ®0=.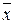

5) Класс линейных функций. Обозначение: L.

L ={ f (x ₁, x ₂,…, x_n)Î P ₂: f (x ₁, x ₂,…, x_n)= c ₀Å c ₁× x ₁Å c ₂× x ₂Å…Å c_n × x_n, где c ₀, c ₁, c ₂,…, c_n равны 0 или 1}. Таким образом, этот класс состоит из тех функций алгебры логики, которые представимы линейным выражением. Различные линейные функции от n переменных отличаются друг от друга составом слагаемых, входящих в их линейные выражения. Этот состав определяется значением коэффициентов: если соответствующий коэффициент равен нулю, то слагаемое отсутствует. И так как число коэффициентов равно n +1, то число функций от n переменных, относящихся к классу L, равно 2 ^{n +1}. Из элементарных функций линейными являются тождественная функция х, отрицание 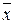, константы 0 и 1, а также Å и º.

Утверждение:

L – замкнутый класс, т.е. [ L ]= L.

Доказательство:

По свойствам замыканий L Í [ L ]. Покажем, что [ L ] Í L. Т.к. х Î[ L ], то достаточно рассмотреть произвольную функцию ФÎ[ L ]. По определению замыкания функция Ф выражается формулой через функции класса L, т.е. Ф= f (f ₁, f ₂,…, f_m), где функции f, f ₁, f ₂,…, f_m Î L. Иными словами функция Ф представляет из себя «линейное выражение от линейных выражений», а оно в свою очередь линейно. Таким образом, функция ФÎ L. И так как Ф – произвольная функция из замыкания, то [ L ] Í L. Следовательно, [ L ] = L.

Лемма о нелинейной функции.

Если функция алгебры логики от n переменных f (x ₁, x ₂,…, x_n) нелинейна, то из неё можно получить х ₁& x ₂ путем подстановки констант 0 или 1 и функций х и 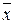, а также, возможно, размещением знака отрицания над f.

Доказательство:

Рассмотрим полином Жегалкина для функции f:
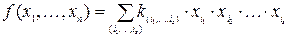. Вследствие нелинейности функции f (x ₁, x ₂,…, x_n) в полиноме обязательно найдется слагаемое, содержащее не менее двух сомножителей. Без уменьшения общности можно считать, что этими сомножителями являются х ₁ и х ₂. Преобразуем полином к виду: = х ₁× х ₂× f ₁(х ₃,…, х_n) Å х ₁× f ₂(х ₃,…, х_n) Å х ₂× f ₃(х ₃,…, х_n) Å
Å f ₄(х ₃,…, х_n). Так как f (x ₁, x ₂,…, x_n) нелинейна, то f ₁(х ₃,…, х_n)¹0 и существует набор значений a ₃,…, a_n такой, что f ₁(a ₃,…, a_n)=1. Подставим этот набор в полином. Тогда f (x ₁, x ₂, a ₃,…, a_n) = х ₁× х ₂× f ₁(a ₃,…, a_n) Å х ₁× f ₂(a ₃,…, a_n) Å
Å х ₂× f ₃(a ₃,…, a_n) Å f ₄(a ₃,…, a_n) = х ₁× х ₂ Å х ₁× a Å х ₂× b Å c, где a, b и с равны нулю или единице. Теперь заменим х ₁ на (х ₁Å b) и х ₂ на (х ₂Å а) – это соответствует подстановке функций вида: х или 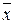, в зависимости от значений a и b. Получим: f (x ₁Å b, x ₂Å а, a ₃,…, a_n) = (х ₁Å b)×(х ₂Å а) Å (х ₁Å b)× a Å (х ₂Å а)× b Å c = = х ₁× х ₂ Å х ₁× a Å х ₂× b Å a × b Å х ₁× a Å a × b Å х ₂× b Å a × b Å c = х ₁× х ₂ Å a × b Å c. К последнему выражению добавим (a × b Å c) – это соответствует возможному размещению знака отрицания над функцией. В итоге будет получена функция двух переменных j (x ₁, x ₂) = х ₁× х ₂ = х ₁ & х ₂. Что и требовалось доказать.

Пусть функция алгебры логики задана полиномом Жегалкина: f (х, y, z, t) = xyz Å yzt Å xy Å zt Å xz Å x Å 1. Здесь для компактности записи пропущен знак «×». Выполним преобразования полинома, как указано в доказательстве леммы: f (х, y, z, t) = xy (z Å 1) Å x (z Å 1) Å yzt Å (zt Å 1). Таким образом, в соответствии с введенными в лемме обозначениями f ₁(z, t) = z Å 1, f ₂(z, t) = z Å 1, f ₃(z, t) = zt, f ₄(z, t) = zt Å 1. Заметим, что f ₁(z, t) = 1 при z = 0 и t = 0 или t = 1. Для определенности рассмотрим набор (z, t) = (0,1). На выбранном наборе f ₂(0,1) = 1, f ₃(0,1) = 0 и f ₄(z, t) = 1, т.е. a, b и с равны соответственно 1, 0 и 1. И f (х, y,0,1) = xy Å x Å 1. Заменим теперь у на у Å 1. Тогда f (х, y Å1,0,1) = x (y Å 1) Å x Å 1= xy Å x Å x Å 1= xy Å 1. Добавим к последнему выражению (a × b Å c)=1 и j (х, у) = х × у. Тем самым, с помощью замены х на х, у на , z на ноль и t на единицу, а также установки знака отрицания над функцией получена конъюнкция.

Таблица 17

	Т0	Т1	S	M	L
	+	–	–	+	+
	–	+	–	+	+
	–	–	+	–	+

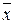
Отметим, что все замкнутые классы попарно различны. Это хорошо видно из таблицы 17, где знаком «+» отмечена принадлежность функций 0, 1 и 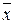к классу, а знаком «–» отсутствие соответствующей функции в классе.

Дата добавления: 2014-01-07