
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пример 1. Принцип максимина в антагонистических играх
|
|
|
|
Принцип максимина в антагонистических играх. Седловая точка
Как отмечалось, важнейшим вопросом в теории игр (в том числе и матричных) является вопрос о выборе оптимальных стратегий для каждого из игроков.
Оптимальной стратегией игрока в матричной игре называется такая, которая обеспечивает ему максимальный выигрыш. Если игра повторяется неоднократно, то оптимальная стратегия должна обеспечивать максимальный средний выигрыш.
При выборе этой стратегии основой рассуждений является предположение, что противник является, по меньшей мере, так же разумен, как и мы сами, и делает все, чтобы добиться такой же цели.
Расчет на разумного противника - лишь одна из возможных позиций в конфликте, но в теории игр именно она кладется в основу.
При этом для выбора оптимальной стратегии используют принцип максимина: выбирай ту стратегию, чтобы при наихудшем для нас поведении противника получить максимальный выигрыш. Другими словами, принцип максимина предполагает выбор той стратегии, при которой наш минимальный выигрыш для различных стратегий максимален. Отсюда и название «принцип максимина».
Как видно, принцип максимина - это принцип крайне осторожного игрока, но именно он является основным принципом теории матричных игр.
Для пояснения принципа максимина рассмотрим пример 1 матричной игры G (4х5) с платежной матрицей, приведенной на рис. 2.2.
 Bj
Ai Bj
Ai
| B1 | B2 | B3 | B4 | B5 | ai | |
| A1 | |||||||
| A2 | |||||||
| A3 | |||||||
 A4 A4
| максимин
 aij aij
| ||||||
| bj | |||||||

| минимакс
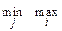 aij aij
|
Рис. 2.2
Какой стратегией игроку А воспользоваться? Есть соблазнительный выигрыш 12, при применении стратегии А 3. Но при этом противник может выбрать стратегию В 3, и игрок А получит выигрыш, равный всего трем.
Для определения оптимальной стратегии в соответствии с принципом максимина, запишем в правом добавочном столбце платежной матрицы минимальное значение a i в каждой строке (минимум строки). Из всех значений a i (правый столбец) выделим наибольшее. Ему соответствует стратегия А 4. Выбрав эту стратегию, мы во всяком случае можем быть уверены, что при любом поведении противника выигрыш будет не менее пяти.
Эта величина - наш гарантированный выигрыш. Он называется нижней ценой игры (или «максимином» - максимальный из минимальных выигрышей). Будем обозначать его a. В нашем примере a =  aij =5.
aij =5.
Теперь станем на точку зрения игрока В и порассуждаем за него. Выбирая стратегию, он хотел бы отдать поменьше, но должен рассчитывать на наихудшее для него поведение игрока А.
Припишем к платежной матрице (рис.2.2) нижнюю строку и в ней запишем наихудшее для игрока В возможные результаты (максимумы столбцов b j.
Очевидно, осторожный противник должен выбрать стратегию, при которой величина b j минимальна. Эта величина называется верхней ценой игры (или “минимаксом” - минимальный из максимальных проигрышей). Будем обозначать ее b. В нашем примере b =  aij = 7.
aij = 7.
Итак, исходя из принципа осторожности, игрок А должен выбрать стратегию А 4, а его противник - В 3. Такие стратегии называются максиминными или минимаксными стратегиями (вытекающие из принципа максимина).
До тех пор, пока обе стороны в нашем примере будут придерживаться своих максиминных стратегий, выигрыш игрока А и проигрыш игрока В будет равен а 43=5.
Случай b = a, соответствует наличию у платежной матрицы так называемой седловой точки.
Определение. Точка (i *, j *) называется седловой точкой платежной матрицы || a ij||, если для всех остальных i и j этой матрицы выполняется условие
ai*j ³ai*j*³ aij*,
т.е. аij является одновременно минимумом своей строки и максимумом своего столбца.
Приведем без доказательства следующую теорему.
Пример 2. Найти решение игры G (3х3), платежная матрица которой имеет следующий вид:
 |
| Bj Ai | B1 | B2 | B3 | a i |
| A1 | -1 | -2 | -2 | |
| A2 | -1 | -1 | ||
| A3 | ||||
| bj |
Определим 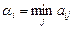 и
и  и запишем их в таблицу.
и запишем их в таблицу.
Нижняя цена игры 
Верхняя цена игры 
Так как a=b=0, то платежная матрица и матричная игра имеют седловую точку. Оптимальными стратегиями для игрока А является стратегия А3, а для игрока В - В3.
Легко заметить, что отклонение игрока А от оптимальной стратегии приводит к уменьшению его выигрыша, а одностороннее отклонение игрока В - к увеличению его проигрыша.
Могут встречаться случаи, когда платежная матрица имеет несколько седловых точек, однако это не изменит характера рекомендуемых решений, поскольку все ситуации равновесия имеют одну и ту же цену, а следовательно, эквиваленты.
Пример 3. Найти решение игры G (3х4), платежная матрица которой имеет вид:
 Bj
Ai Bj
Ai
| B1 | B2 | B3 | B4 | a i |
| A1 | |||||
| A2 | |||||
| A3 | |||||
| b j |
Определим a i и bj и запишем их в таблицу.
Находим нижнюю и верхнюю цену игры:
 ;
;  . Видно, что игра имеет четыре седловые точки с соответствующими парами оптимальных стратегий: А1В2; А1В4; А3В2 и А3В4. Цена игры равна 6.
. Видно, что игра имеет четыре седловые точки с соответствующими парами оптимальных стратегий: А1В2; А1В4; А3В2 и А3В4. Цена игры равна 6.
В заключение отметим, что с позиций игрока 1 второй игрок руководствуется принципом минимакса, обеспечивающим минимизацию максимальных потерь. Но с собственной точки зрения игрока 2, оценивающего свой выигрыш, он также руководствуется принципом максимина. Поэтому, как правило, говорят лишь об использовании в антагонистической игре принципа максимина обоими игроками.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 559; Нарушение авторских прав?; Мы поможем в написании вашей работы!