Рост зародыша новой фазы

Зарождение (гомогенное и гетерогенное) частиц новой фазы в сплавах;

Часть 2. Фазовые превращения в конденсированных средах (жидкое и твердое состояние)

В физике фазовых превращений в сплавах принято, в соответствии с теорией Гиббса, что зарождение частиц новой фазы происходит за счет результирующего уменьшения свободной энергии системы при наличии соответствующих флуктуаций.

Гиббс проводит следующее различие между двумя типами флуктуаций:

1) представляющих значительные перегруппировки атомов в небольших объемах;

2) переставляющих незначительные перегруппировки атомов в больших объемах;

Обычно зарождение новой фазы начинается с образования физически различимых центров, после чего претерпевшие превращение данные области растут в окружающую их среду.

Таким образом, данный процесс в определенном смысле является гетерогенным, так как во время превращения в системе появляются новые поверхности (межфазные границы). Вместе с тем, в соответствии с теорией фазовых превращений данный процесс относится к гомогенному зарождению.

Гетерогенное зарождение реализуется при зарождении частиц новой фазы в определенных локальных местах структуры матричной фазы, характеризующихся повышенным (относительно среднего) уровнем свободной энергии.

В классической теории фазовых превращений образование зародышей обычно рассматривается в ракурсе флуктуаций первого типа, то есть любая система в достаточно малом объеме будет находиться в устойчивом состоянии относительно таких флуктуаций.

Это связано с тем, что при фазовых превращениях отрицательному по знаку изменению свободной энергии, обусловленному образованием некоторого объема более стабильной фазы, противостоит положительное по знаку изменение свободной энергии, связанное с появлением межфазной границы.

Рассмотрим в качестве примера следующий простой случай (полиморфное превращение):

Бинарный сплав (состава С = С1) охлажден (рис.8) с температуры Т0 (однофазная область - а - фаза) до температуры Т1 (однофазная область - в - фаза), то есть при образовании зародыша новой фазы в данном случае не происходит изменение концентрации в области превращения, а только перестраивается кристаллическая решетка матричной фазы.

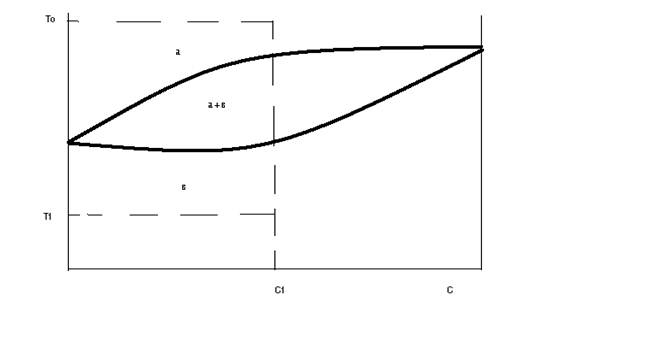
Рис.8. Диаграмма состояния (схема).

При образовании сферического зародыша в- фазы выражение для свободной энергии системы будет иметь следующий вид:

G = n (μв - μа) + σ S + n ∆gs,

где n - число атомов в зародыше;

μв - μа - химические потенциалы компонента в фазах в и а;

n∆gs - результирующая энергия, связанная с возникновением упругой деформации;

σ - коэффициент поверхностного натяжения;

S - площадь поверхности зародыша.

Учитывая, что

n = Vз/Vaт = 4 (π R³)/3 Vaт, S= 4πR²

(Vз - объем зародыша, Vaт - средний объем атома)

G(R) = 4π R³ (μв - μа + ∆gs)/ 3Vaт + 4π σ R²

Данная зависимость G(R) будет иметь максимум в точке R=Rk (критический радиус зародыша)

Rk = - 2σ Vaт/(μв - μа + ∆gs) = 2σ Vaт/gэф,

где gэф = - (μв - μа + ∆gs) = (μа - μв - ∆gs) – эффективная движущая сила.

Поскольку для реализации процесса фазового превращения эффективная движущая сила должна иметь положительное значение, то

μа > μв+ ∆gs.

В соответствии с зависимостью функции G(R) от радиуса образующейся частицы новой фазы, точка R=Rk является координатой неустойчивого равновесия зародыша:

при R < Rk - зародыш растворяется;

при R > Rk - зародыш растет.

Причем величина критического радиуса зародышей смещается в сторону больших значений при увеличении коэффициента поверхностного натяжения σ и уменьшении эффективной движущей силы gэф.

Это очень существенный момент, поскольку величина критического радиуса определяет, согласно теории Бекера – Деринга, стационарную скорость (или вероятность) образования зародышей

Iv ~ exp -λ (R k)²/кT (λ – коэффициент),

которая уменьшается по мере возрастания Rk.

В свою очередь, величина σ и ∆gs (соответственно и в целом gэф) в значительной степени зависит от класса межфазной границы, что связано с соответствием сопряжения кристаллической решетки матричной фазы с кристаллической решеткой образовавшейся фазы.

Межфазные границы делятся на три основных класса: когерентные, полукогерентные, некогерентные.

Когерентными считаются границы, когда плоскость раздела фаз является общей для их решеток. В общем случае, когда неточность сопряжения решеток соприкасающихся фаз невелика, когерентность обеспечивается за счет упругой деформации.

Полукогерентными считаются межфазные границы (сопоставимые с малоугловой границей зерна), на отдельных участках которой в результате упругой деформации наблюдается когерентность, на других же участках постепенно накапливается несоответствие, которое периодически устраняется за счет возникновения разрыва.

Некогерентным считаются межфазные границы, имеющие сильное разупорядочение (сопоставимо с большеугловой границей зерна).

Таким образом, в случае образования когерентных зародышей, коэффициент поверхностного натяжения мал, а упругая энергия, наоборот, велика.

Некогерентные зародыши имеют значительно большую величину коэффициента поверхностного натяжения, но меньшую упругую энергию.

В случае, когда в системе образуются зародыши химического соединения (карбиды, нитриды, интерметаллиды и т.п.) зависимость стационарной скорости образования зародышей от критического радиуса, полученная Бекером – Дерингом, сохраняется.

Равновесное состояние между твердым раствором (например, некой γ-фазой) и химическим соединением AmBn, образованным в соответствии с реакцией

mA + nB=AmBn

описывается следующим выражением, являющимся уравнением линии растворимости, которая ограничивает двухфазную область (γ + AmBn):

m ln(aA)р + n ln(aB)р = ∆GAmBn,

где (aA)р и (aB)р – термодинамические активности компонентов А и В в твердом растворе в условиях равновесия с соединением AmBn;

∆GAmBn – свободная энергия образования соединения AmBn.

При этом следует отметить, что хотя зависимость критического размера зародыша соединения от эффективной движущейся силы сохраняет тот же вид

Rk = 2σVм/gэф (Vм - объем молекулы),

но эффективной движущей силой gэф в данном случае будет наличие пересыщения твердого раствора, поскольку в твердом растворе концентрация компонента А, сразу после охлаждения γ-фазы из однофазной области до температуры существования двухфазной области, больше своего равновесного значения и с данного момента времени начинается процесс образования новой фазы:

gэф = кТ[m ln(aA) + n ln(aB) - m ln(aA)р + n ln(aB)р - ∆gs/кТ] =

кТ[m ln(aA) + n ln(aB) - (∆GAmBn + ∆gs)/кТ],

где [m ln(aA) + n ln(aB)] – текущее «произведение активности» компонентов А и В в твердом растворе в условиях формирования зародышей химического соединения и соответственно двухфазной области соответствует началу процесса образования.

Из анализа данного выражения для эффективной движущей силы, следует, подобному ранее приведенному, что критический радиус зародыша имеет положительное значение (Rk > 0) при условии gэф>0, которое выполняется, когда

m ln(aA) + n ln(aB) > (∆GAmBn + ∆gs)/кТ

При этом характер зависимости размера критического радиуса зародыша от величины поверхностной энергии и энергии упругой деформации качественно остается неизменным.

Как уже указывалось ранее, повышение уровня когерентности межфазной границы в большинстве случаев не только понижает поверхностную энергию (положительный эффект), но и повышает энергию упругой деформации (отрицательный эффект).

Однако, в принципе, можно разработать стали и сплавы такого химического состава, что образующиеся в твердом растворе когерентные мелкодисперсные частицы химических соединений практически только снижают поверхностную энергию. Например, в структуре жаропрочных аустенитных никелевых сплавов присутствуют когерентные мелкодисперсные частицы гамма штрих - фазы, с периодом кристаллической решетки всего на 0,1% отличающейся периода решетки аустенита.

Рассмотренные теории относятся к случаю «гомогенного» зарождения. Однако может быть сделано формальное расширение данной теории и для описания «гетерогенного» зарождения, когда зародыши образуются на межзеренных границах, дефектах упаковки или дислокациях, путем учета следующего обстоятельства: энергия образования зародыша понижается за счет поверхностной энергии этих дефектов.

Теория фазовых превращений рассматривает два основных типа механизма роста зародышей новой фазы:

- нормальный механизм роста,

- диффузионный механизм роста.

При реализации нормального механизма роста зародыша отсутствует диффузионный подвод (отвод) вещества к межфазной границе по причине, например, недостаточно высокой для эффективной реализации процесса диффузии температуры, отсутствия градиента концентрации (в матричной фазе) в силу равенства концентраций компонентов в матричной фазе и образующейся фазе. К последнему случаю относится пример фазового превращения, рассмотренный в 2.1.

При некогерентной межфазной границе (∆gs=0) эффективная движущая сила имеет вид

gэф = (μа - μв)

и, таким образом, рост частицы новой в-фазы происходит в результате наличия разности химических потенциалов компонентов в матричной фазе и образующейся фазе (не меняющейся во времени процесса) путем перестройки кристаллической структуры матричной фазы.

Соответственно скорость роста частиц радиуса

dR/dt = kgэф = const (k - кинетический коэффициент)

R(t) ~ t

При превращениях, связанных с переносом вещества из твердого раствора в частицу диффузионным путем, процесс роста частиц новой фазы должен описываться уравнением диффузии

∂C/∂t = div D grad С

Для рассматриваемого в 2.1 примера образования в пересыщенном твердом растворе зародышей химического соединения и с учетом сферической формой частиц, а также постоянства коэффициента диффузии, уравнение диффузии имеет следующий вид:

∂С/∂t = D [∂²С/∂r² + (2/r) ∂С/∂r], r > R

где C(r,t) - концентрация компонента В матричной фазе γ,

D - коэффициент диффузии компонента В в γ - фазе,

R(t) - радиус частицы AmBn

В силу того, что уравнение диффузии при наличии в задаче подвижной во времени границы R(t) является в общем случае нелинейным (так называемая задача Стефана) и решение может быть получено только численным путем.

Вместе с тем, во многих случаях системно исследовать аналитическое решение, пусть приближенное, значительно проще и эффективнее, чем анализировать численное решение таких многопараметрических задач.

Обычно, для получения аналитического решения задачи Стефана, пользуются рядом упрощений. Наиболее распространенными являются следующие допущения:

- коэффициент диффузии не зависит от времени, координаты и концентрации;

- рост отдельных частиц рассматривается в матричной фазе бесконечных размеров, то есть не учитывается диффузионное взаимодействие между растущими частицами, что не дает возможность рассмотрения процесса роста частиц на всех его временных этапах, включая асимптотику процесса (большие времена);

- не учитывается влияние поверхностной энергии частицы на условия равновесия между матричной фазой (твердый раствор) и соединением.

Для решения уравнения диффузии необходимо задать начальное и граничные условия:

C(r,0), C(R(t),t), C(∞,t)

Начальная концентрация C(r,0) должна соответствовать концентрации компонента В в исходной матричной γ-фазе:

C(r,0)=Со

Поскольку рассматривается случай роста частиц, лимитируемого диффузией, то из интуитивных соображений принимается, что концентрация компонента В в твердом растворе на межфазной границе соответствует равновесной концентрации на диаграмме состояния:

С(R(t),t)= С(р)

С учетом того, что используется приближение «бесконечной матрицы», второе граничное условие будет иметь следующий вид:

C(∞,t)= Со

(то есть соответствует начальному условию C(r,0)).

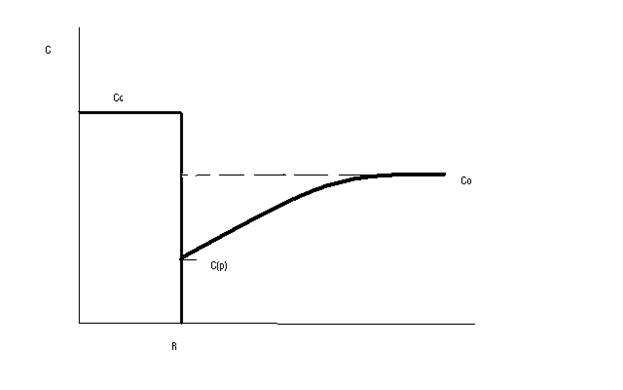
Рис.9.Схематическое распределение концентрации компонента В в зоне роста частицы AmBn (Сс - концентрация компонента В в химическом соединении AmBn).

При росте частицы по параболическому закону

R=2 β √(Dt)

Уравнение диффузии с указанными граничными и начальными условиями имеет точное автомо дельное решение:

(С(r,t) – Co)/(C(р) – Cо) =

[(2 β √(Dt)/r)exp(- r²/4Dt) - √π erfc(r/2√Dt)]/ [(1/ β)exp(-β²) - √π erfc(β)];

где erfc(z) = 1 – erf(z), erf(z) – функция ошибок (табулированная функция).

Постоянная скорости роста β определяется из уравнения баланса на межфазной границе:

(Сс - C(р))dR/dt = D∂С/∂r|r=R

После подстановки решения уравнения диффузии C(r,t) в уравнение баланса массы получается трансцендентное уравнения для определения β - корня следующего уравнения:

F(β) = (Cо - C(р))/(Cc - C(р)) = 2 β²[1 - √π exp(β²) erfc(β)]

График функции F(β) приведен на рис.10.

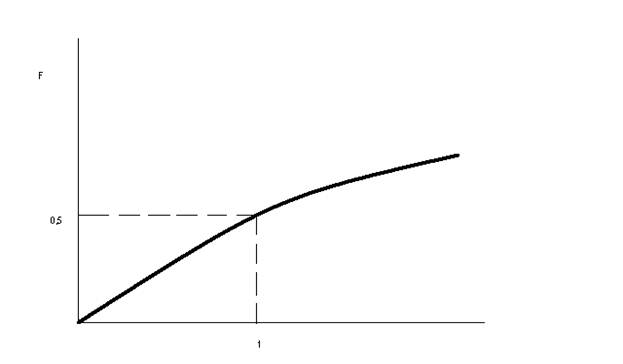
Рис.10. График зависимости F(β) от β.

Из данного графика видно, что в случае

F(β) = (Cо - C(р))/(Cc - C(р)) < 0,5,

для определения β можно использовать линейную функцию

F(β) = 0,5 β

Концентрация компонента В в исходной матричной фазе Со и его содержание в соединении Сс известны, а равновесная концентрация C(р) находится из диаграммы состояния для заданной температуры процесса.

Кроме того, зная β, можно определить (при известном значении коэффициента диффузии) и скорость роста частиц соединения по формуле

dR/dt = β√ (D/t)

Довольно часто данную формулу используют для решения обратной задачи, когда при известной скорости роста частиц соединения определяется коэффициент диффузии. Конечно, в принципе это возможно, но необходимо учитывать, что такой подход является приемлемым только для случая автомодельного решения уравнения диффузии, то есть экспериментально должно быть установлено соответствие зависимости скорости частиц от времени формуле, приведенной выше.

2.3. Коалесценция (теория Лифшица – Слезова)

В диффузионном процессе формирования новой фазы при распаде пересыщенного твердого раствора следует учитывать, что, наряду со стадиями зарождения и роста частиц, существует стадия коалесценции.

На первых двух стадиях происходит флуктуационное образование зародышей новой фазы и их дальнейший рост непосредственно из твердого раствора.

На стадии роста частиц новой фазы, когда их размер уже достаточно большой, а при этом, пересыщение твердого раствора матричной фазы становится чрезвычайно малым и флуктуационное зарождение практически исключено (критический размер зародышей должен достигать макроскопической величины), превалирующим является процесс коалесценции.

Механизм процесса коалесценции заключается в росте крупных частиц за счет растворения мелких частиц, в результате чего на асимптотике процесса суммарный объем частиц новой фазы остается неизменным.

В основе общепринятой мировым научным сообществом теории коалесценции Лифшица – Слезова лежат следующие постулаты:

- асимптотика процесса (большие времена) не зависит от начальной функции распределения частиц по размерам;

- наличие упругой деформации частиц не учитывается, то есть рассматривается случай некогерентных и полукогерентных межфазных границ;

- форма частиц принята сферической, поскольку учет несферичности частиц качественно не влияет на кинетику процесса;

- рассматривается процесс в бинарной (или квазибинарной) системе;

- равновесная концентрация в твердом растворе на межфазной границе между частицей новой фазы и матричной фазой соответствует уравнению Гиббса – Томпсона (твердые растворы соответствуют «идеальным твердым растворам», когда термодинамическая активность равна концентрации данного компонента);

- процесс диффузии рассматривается в квазистационарном приближении.

В соответствии с данными допущениями описание процесса коалесценции проводится на основе решения следующей системы уравнений:

1. Уравнение диффузии (квазистационарный вариант)

D [∂²С/∂r² + (2/r) ∂С/∂r] = 0,

решение которого имеет вид

С=Cср+(CR– Cср)R/r,

где Cср - средняя концентрация рассматриваемого компонента в твердом растворе,

CR - концентрация рассматриваемого компонента в твердом растворе на границе с частицей,

R - радиус частицы.

Дата добавления: 2014-01-07