I.1. Общая характеристика нелинейных систем

I. НЕЛИНЕЙНЫЕ СИСТЕМЫ УПРАВЛЕНИЯ

Основная особенность нелинейных систем заключается в том, что они не удовлетворяют принципу суперпозиции. Математические модели нелинейных систем – это системы нелинейных дифференциальных или алгебраических уравнений. Эти модели также делятся на модели вход – выход и модели в переменных состояния. Модель вход – выход может иметь вид, например:

(I.1)

где 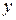, , 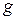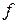– векторы выходных величин, входных задающих воздействий и возмущений, 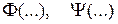– нелинейные функции. Модели нелинейных систем в переменных состояния в общем случае это система уравнений

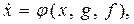(I.2)

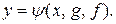(I.3)

где – некоторые нелинейные вектор-функции; – вектор состояния.

Обычно в нелинейных системах можно выделить ряд линейных и ряд существенно нелинейных элементов. Деление на линейные и нелинейные элементы или системы достаточно условно. Обычно под существенно нелинейными элементами или системами понимают такие, которые при сформулированных требованиях к точности их описания не могут быть описаны линейными дифференциальными или алгебраическими уравнениями. Если в этих условиях некоторый элемент (нелинейный) может быть описан линейной моделью, то он называется линейным. Возможность описания системы линейной или нелинейной моделью связана либо с величиной отклонений переменных системы от их установившихся значений, либо с не дифференцируемостью (не гладкостью) нелинейных характеристик её элементов.

Так как нелинейности могут быть весьма сложного вида, то нелинейная система в общем случае может иметь несколько положений равновесия. Поэтому понятие устойчивости движения в случае нелинейных систем трансформируется в понятие устойчивости положений равновесия. При этом разные положения равновесия одной и той же системы могут иметь разный характер по устойчивости. В связи с этим, в теории нелинейных систем вводятся понятия устойчивости в малом, устойчивости в большом, устойчивости в целом и ряд других понятий устойчивости.

Существенным фактом является то, что нелинейные системы могут быть работоспособны и при наличии неустойчивых положений равновесия, а некоторые нелинейные системы работоспособны только при таких положениях равновесия. Нелинейные системы в установившемся режиме могут совершать периодические и хаотические (типа случайных возмущений) движения. Хаотические движения нелинейных систем характеризуются тем, что они ограничены по амплитуде, но никогда не повторяются и не затухают. Интервалы возрастания и убывания переменных системы при её хаотическом движении чередуются, но все время меняются по длительности.

Из-за сложности нелинейных дифференциальных уравнений в настоящее время нет единого метода анализа нелинейных динамических систем. Теория этих систем – это совокупность методов анализа и синтеза, каждый из которых разработан применительно к некоторому классу нелинейных систем.

Дата добавления: 2014-01-07