Оценка абсолютной устойчивости нелинейных систем по критерию Попова

Критерий абсолютной устойчивости Попова дает достаточное условие абсолютной устойчивости нелинейной системы с одной однозначной нелинейностью.

Критерий Попова основан, как и критерий Найквиста, на использовании амплитудно-фазовой характеристики и имеет простую геометрическую интерпретацию.

Пусть в контуре нелинейной системы содержится нелинейный элемент с характеристикой , имеющей любую конфигурацию, но не выходящей за пределы определенного сектора [0, k_H]

Рис. 4.55.

Линейная часть имеет амплитудно-фазовую характеристику:

(4.60)

На основе данной характеристики строится модифицированная амплитудно-фазовая характеристика:

, (4.61)

где 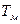- коэффициент масштабирования (обычно берется равным единице).

Тогда критерий Попова формулируется следующим образом:

Для абсолютной устойчивости нелинейных систем одного класса, характеризующихся прямой с наклоном К_Н, достаточно чтобы модифицированная АФХ не охватывала точку (-1/К_н;j0) и через эту точку можно было бы провести прямую так, чтобы модифицированная амплитудно-фазовая характеристика не пересекала эту кривую и осталась справа.

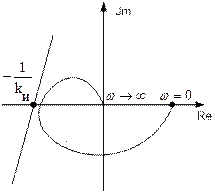
Рис. 4.56.

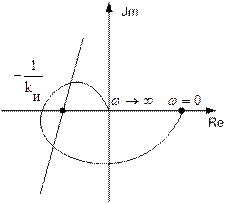
Рис. 4.57.

Рис. 4.58.

Нетрудно заметить, что в соответствии с критерием Попова система (Рис. 4. 56) абсолютно устойчива, а системы (Рис. 4.57, 4.58) не являются абсолютно устойчивыми.

Критерий Попова может быть использован и при обратной задаче - выборе нелинейных элементов в нелинейной системе. В данном случае выбор нелинейного элемента не должен влиять на устойчивость системы.

Данная задача решается следующим образом: строится модифицированная амплитудно-фазовая характеристика и проводится прямая наиболее близкая к этой характеристике. Точка пересечения этой прямой с осью абсцисс определяет коэффициент наклона К_н, а значит и класс нелинейных характеристик.

ПРИМЕР

Пусть дана нелинейная система. Линейная часть представлена передаточной функцией с параметрами . Нелинейный элемент - двухпозиционное реле с параметрами . Определить является ли данная система абсолютно устойчивой.

Определим коэффициент наклона

Построив модифицированную амплитудно-фазовую характеристику, нетрудно, что МАФХ пересекает ось абсцисс в точке (-0,11;j0) и что через точку (-0,125;j0) можно провести прямую, не пересекающую модифицированную амплитудно-фазовую характеристику (Рис. 4.59).

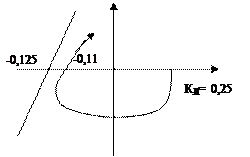Рис. 4.59

Определим допустимое значение параметра 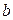, при котором система абсолютно устойчива.

МАФХ пересекает ось абсцисс в точке (-0,11;j0). Следовательно, критическое значение параметра определится следующим образом:

То есть при параметре 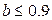система не будет абсолютна устойчива.

Дата добавления: 2014-01-07