Теории изгиба жестких плит

Плита называется жесткой, если ее прогибы малы по сравнению с толщиной. Если прогибы велики, то при жестком закреплении кромок появляются силы растяжения плиты, так как размеры плиты по ширине увеличиваются, что означает наличие сил растяжения.

Решение ищется в перемещениях:

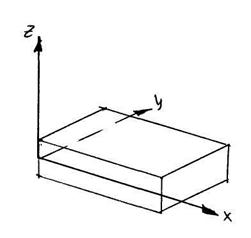
Разложим функции в ряд Маклорена:

Из анализа картины деформаций элемента плиты можно заключить, что точки срединной поверхности в плоскости пластины не перемещаются (срединная поверхность z=0).

Так как толщина плиты мала, то z тоже мал, поэтому можно написать, что:

Эти упрощенные соотношения называются гипотезами Кирхгоффа-Лява (геометрические гипотезы).

Для дальнейшего упрощения u_x1, u_y1 выражают через u_z0 из геометрических соображений.

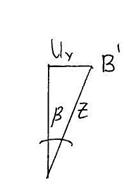
Из рисунка видно, что a=b, так как это углы с перпендикулярными сторонами.

Так как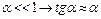

Согласно гипотезам Кирхгофа-Лява:

Аналогично 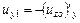(так же из гипотезы Кирхгофа-Лява)

И формулируется: нормаль остается нормалью, и после деформации

Для простоты вводятся обозначения: через w обозначают u’_zo(x,y), тогда:

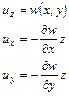
Таким образом перемещения любой точки пластины нам известны, тогда можно вычислить деформации по соотношениям Коши, а затем напряжения по соотношениям закона Гука:

Остальные деформации:

Эти соотношения примерны, так как мы оборвали ряд Маклорена, на самом деле деформации по z существуют.

Кирхгоф и Ляв приняли следствие как гипотезу и на сегодня они звучат следующим образом:

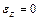- поперечных деформаций нет

Это предположение является противоречивым, так как при продольном растяжении-сжатии элемента тела появляются поперечные деформации в виду эффекта Пуассона, но в совокупности, в целом для тела, это соотношение является справедливым.

Второе противоречие:

Но это полное противоречие формуле Журавского, согласно ей

Это противоречие есть следствие приближенности выражений для перемещений (оборван ряд Маклорена). Как показали эксперименты, и точные решения на максимальные напряжения они не влияют.

Вывод уравнения для определения функции w

Используем следующие выражения:

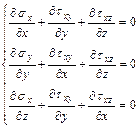
Используем закон Гука:

Теоретически было доказано, что:

и аналогично

- статические гипотезы Кирхгофа-Лява. (Проверку их для балки смотри в предыдущей лекции)

Воспользуемся первым соотношением из статических гипотез, получим:

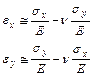
Но в уравнениях равновесия σ_z,t_yz,t_xz отбрасывать нельзя, поскольку производная это тангенс угла наклона, то даже при малости функции угол её наклона может оказаться очень большим.

Из закона Гука легко найти σ_х:

e_х и e_у выразим через w и получим:

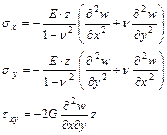
Для изотропного материала , тогда, подставим это в первые два уравнения равновесия. После подстановки получим:

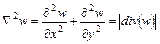, отсюда можно найти t_xz, t_yz:

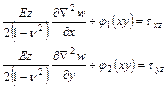
Для отыскания j₁, j₂ используем уравнения равновесия граничных элементов

При z=

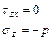
Подставим в полученные уравнения:

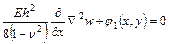
Аналогично из уравнения равновесия другого граничного элемента получаем:

Проверим выполняются ли уравнения равновесия граничных элементов, которые примыкают к нижней грани, где z=- , здесь z²=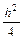, поэтому уравнения равновесия выполняются автоматически.

Удовлетворим третье уравнение равновесия:

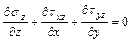подставим сюда выражения для t_xz, σ_yz с учетом j₁, j₂

Найдем σ_z, проинтегрировав это уравнение:

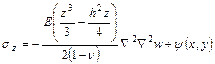
Как и ранее ψ(х,у) определяем из уравнений равновесия граничных элементов:

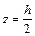
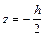
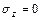
Из второго условия получим:

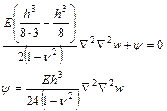
Введем обозначение: 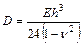- цилиндрическая жесткость

Уравнение для w получим из условия при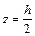

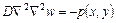- уравнение Софи-Жермен (получено в 1816 году).

Достоинства и недостатки полученной теории пластин:

+ Нужно находить только одну функцию w, через нее вычисляются все деформации и напряжения

+ w имеет физический смысл – это прогиб пластины, поэтому можно решение отыскивать по экспериментальным данным

- согласно теории e_z=0 так как , из положения выходят с помощью закона Гука: , поэтому e_z можно вычислить

- это противоречие решается с помощью уравнений равновесия 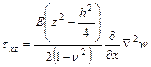, 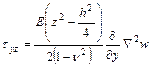- это аналоги формулы Журавского

- При подсчете реактивных сил шарнирно опертой пластины в углах расчеты дают сосредоточенные силы, так как сосредоточенных сил в природе не существует, то это противоречит основам теории упругости, теория Кирхгофа-Лява позволяет получать хорошие решения только внутри области пластины, вблизи края решение может сильно отличаться от истинного, поэтому использовать решение задачи о пластине в рамках гипотез Кирхгофа-Лява не допустимо для расчета опор пластины

- Возникают трудности при формулировке уравнений равновесия граничных элементов, примыкающих к торцам пластины

Уравнения равновесия граничных элементов

Уравнения Софи-Жермен это уравнения равновесия внутреннего элемента в виде . Кроме этого уравнения необходимо чтобы выполнялись уравнения равновесия граничных элементов. Они зависят от условий закрепления: если по краям пластина заделана, то на эти края действуют реактивные силы и записать уравнения равновесия невозможно. Можно записать только условия закрепления.

Заделка - уравнений равновесия граничных элементов нет.

Схема свободного опирания.

Если пластина свободно оперта по краям уравнения равновесия возможно записать.

Вырежем и рассмотрим граничный элемент, на него воздействует реактивная сила опоры.

Снова видно, что условия равновесия записать в явном виде нельзя.

Составим другие условия равновесия:

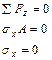
- третий случай опирания.

Рассмотрим граничный элемент:

Выражение для t_xz было получено ранее:

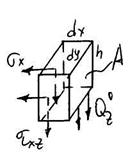
Так как выражение для t_xz содержит z, то есть t_xz зависти от z (переменного по высоте), поэтому его равнодействующую искать простым умножением на площадь не допустимо. Поэтому разбиваем площадь А на элементарные площадки dA, на каждой из них находим равнодействующую t_xz и, суммируя, получим:

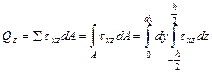
Так как при изменении у t_xz почти не меняется подставляем этот результат в уравнение равновесия. Преобразуем уравнения равновесия, получим:

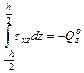
Подставляя сюда выражения для t_xz получим алгебраическое уравнение относительно третьих производных w.

Дата добавления: 2014-01-07