Условия закрепления

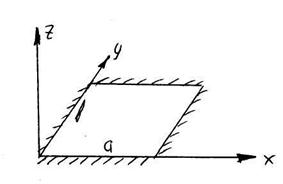
На границе w =0. Левая граница х=0 у – любая, правая х=а у – любая, передняя у=0 х – любая, задняя у=b х – любая. Кроме того угол наклона a=0 на границах.

Угол наклона определяется как tga=w’_x, так как a=0 w’_x=0, аналогично на передней и задней границах.

w=0 на границах w’_x¹0.

Точные решения задачи об изгибе жестких пластин

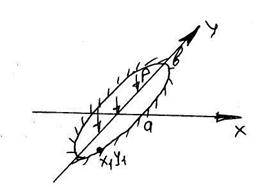
1. Решение имеет вид

Где a, b - полуоси эллипса

D – цилиндрическая жесткость пластины

B – константа, которая вычисляется из уравнения Софи-Жермен

Проверим выполнение условий закреплений:

Если взять точку на границе, то для нее выполняется уравнение эллипса подставляя это в уравнение для w, видим w=0 в точке х₁, у₁

Проверим выполнение условия w’_x=0

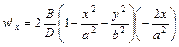подставим сюда уравнение эллипса для точки х₁, у₁ получаем w’_x=0, аналогично для w’_у=0.

Найдем В из уравнения Софи-Жермен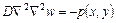

Здесь p(x,y)=const решение можно найти только для этого случая.

2. Задача о свободно опертой прямоугольной пластине под нагрузкой образованной сыпучим материалом. Оказалось, что из всех аппроксимаций нагрузки от сыпучего материала наиболее удачной является следующая:

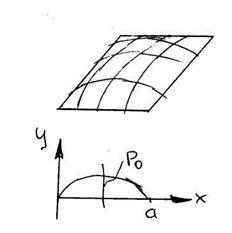
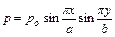
Запишем уравнение Софи-Жермен:

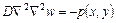
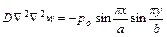
Очевидно, что w надо искать в виде:

В результате получим:

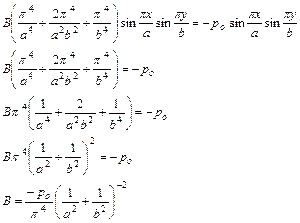
Проверим выполняются ли условия закрепления и уравнения равновесия граничных элементов:

- на границе

Условия закрепления выполняются на правом краю х=а σ_х=0 при любом у

При х=а 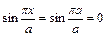отсюда σ_хº0. Аналогично на других границах и уравнения равновесия граничных элементов выполняются.

Так как все уравнения и закрепления выполняются, то решение точное.

Решение задачи изгиба пластины свободно опертой по краям при произвольной нагрузке Р (метод Бубнова-Галеркина):

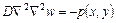
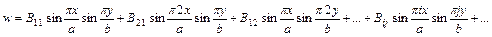
Подставляя, получим:

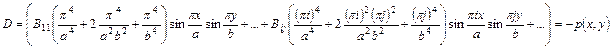
для получения алгебраических уравнений относительно В₁₁,В₂₂… можно использовать любые методы (коллокаций), но наиболее удобным является метод Бубнова-Галеркина. Причина в том, что в методе Бубнова сразу получаются выражения для B_ij.

Умножим это уравнение на 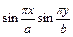, проинтегрируем по площади пластины:

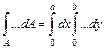
Справа получим: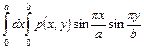

Рассмотрим левую часть:

Оказывается, что все слагаемые кроме первого равны нулю, причем

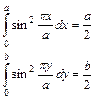
Таким образом получаем:

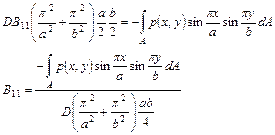
Остальные коэффициенты получаются аналогично.

Изгиб пластины под сосредоточенными силами

Координаты точек приложения сил будем считать известными.

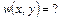
Имеем уравнение равновесия: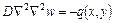

Заменим Р равномерной нагрузкой q, которая распределена по бесконечно малой площадке.

Из условия эквивалентности получаем , в остальных точках q=0:

Подставим в задачу Бубнова-Галеркина:

В правой части q=0 везде кроме этой микроплощадки, получаем:

Таким образом правая часть в случае сосредоточенных сил сразу вычисляется, без интегрирования.

Пластина на упругом основании

Сопротивление грунта обозначим реакцией r(x,y), как видим, к внешней нагрузке добавляется реакция r, поэтому уравнение равновесия принимает вид:

Закон для определения r в простейшем случае имеет вид:

r =-kw – закон Винклера

где k – коэффициент постели

В случае шарнирного опирания w можно искать в виде:

A_ij наиболее удобно находить методом Бубнова-Галеркина

Примечание: как и в случае с балкой, если вес плиты не достаточен по отношению к сосредоточенной силе, плита может приподниматься над грунтом, что непозволительно для дорожных полотен или площадок (посадочных, парковочных).

Задача Фламана

Это расчетная схема давления на грунт ленточного фундамента:

Из математики известно, что в линейной системе уравнений решение единственно.

Анализ решения:

1. при приближении к точкам приложения силы P

Это означает, что вблизи точек приложения силы P использовать решение для расчета на прочность грунта бессмысленно, поэтому решение используется, только для расчета задачи о сдвиге массивов грунта по линиям скольжения(линиям осыпания, потери сцепления).

2. это решение можно использовать для определения поля напряжений при воздействии распределенной нагрузки q(x).

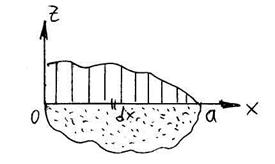
Использование решения задачи Фламана в задаче о действии внешнего давления

Дано: q(x)

Найти: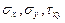

Возьмем площадку dx и от распределенной нагрузки перейдем к сосредоточенной силе dP=q•dx, получаем задачу Фламана.

Для силы dP решение у нас есть:

Такие же решения получим для других отрезков dx, расположенных в других метах. Общее воздействия получим суммируя напряжения от различных dP.

Пример:

В этом случае бесконечных напряжений под нагрузкой не возникает, поэтому при расчете ленточных фундаментов сосредоточенную силу заменяют нагрузкой q более близкой к реальному распределенному давлению в основании.

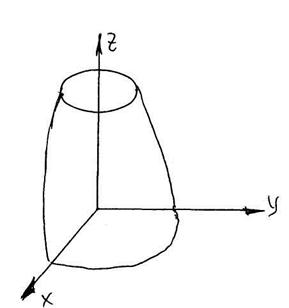
Осесимметричные задачи теории упругости

 

Они возникают при расчете тел вращения. для упрощения задачи переходят к полярной системе координат:

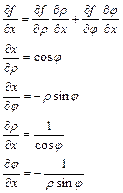
Подставляя вместо производных по х, у производные по r, j с помощью этого соотношения получим новые системы уравнений в полярной системе координат. В случае осесимметричных задач состояние тела не зависит от угла j. То есть производные по j=0 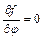, поэтому все уравнения сильно упрощаются. В системе координат х, у была введена функция Эри, через которые вычисляются напряжения:

Аналогичную функцию можно ввести в полярной системе координат:

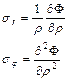
При этом уравнение равновесия внутреннего элемента будут удовлетворяться, остается удовлетворить уравнения равновесия граничных элементов и условия совместности деформаций. Последние принимают вид:

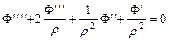, где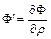

Общее решение этого уравнения можно найти в справочниках.

Самую большую трудность в теории упругости всегда составляет удовлетворение уравнений равновесия элементов на границе и условий закрепления, но для ряда задач удается получить точное решение.

Задача о трубе

С_i – константы интегрирования уравнения

Внешнее давление:

Так как R>r ® C₃<0 и ½ С₂ ½<½ C₃ ½, поэтому видно, что s₂ уменьшается к центру, s₃ наоборот увеличивается к центру, чтобы проверить на прочность надо вычислить

Форма кривой s_эфф сильно зависит от отношения

Задача Кирша

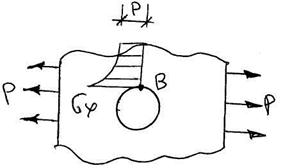
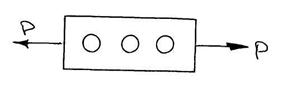
Система уравнений в полярной системе координат позволяет легко решить и кососимметричные задачи. Одной из них является задача о растяжении пластины с отверстием (пластина считается бесконечной). Задача Кирша знаменита тем, что позволяет найти s_j,max. Оказывается, что s_j,max=3р не зависимо ни от размеров ни от упругих характеристик материала, оно возникает в точке В.

Задачи подобного типа для разных видов отверстий называются задачами о концентрации напряжений.

Следствие: при расчете даже простых с круговыми отверстиями независимо от размера отверстия мы должны уменьшать допустимое напряжение в 3 раза.

Задачи термоупругости

- закон Дюгамеля-Неймана или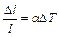

Запишем обобщенный закон Гука:

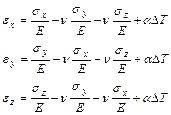
Для изотропного тела:

…

Так как aDТ=const, то в уравнениях внутренних элементов aDТ не участвует так как (aDТ)’=0.

aDТ входит только в уравнения равновесия граничных элементов и условия закрепления, если их выражаем через деформации. Аналогично задачи о трубе под давлением точное решение получено для задачи о трубе при наличии перепада температур:

Это случай, когда нагревается наружный слой.

Примечание: в отличие от простых тел, типа параллелепипед, некоторые конструкции получают температурные напряжения с большими перепадами от сжимающих до растягивающих. Особенно большие перепады появляются в тех случаях, когда учитываются процессы теплопроводности, то есть процесс перетекания тепла из одной точки в другую, это уравнение имеет сложный вид:

,

И практически не имеет точных решений. l- коэффициент отражающий способность к переносу тепла, F-внутренний источник тепла, поэтому эти задачи могут быть решены только приблизительно.

Дата добавления: 2014-01-07