Распределение Пуассона. Дискретная случайная величина Х имеет распределение Пуассона, если её возможные значения: 0,1,2, ,k, (счетное множество значений)

Дискретная случайная величина Х имеет распределение Пуассона, если её возможные значения: 0,1,2,…, k,… (счетное множество значений), а соответствующие вероятности выражаются формулой Пуассона ,

По закону Пуассона распределены с.в., подчиняющиеся схеме Бернулли, но когда n ®¥ и р ®0 так, что a=np – постоянно. По закону Пуассона распределены числа так называемых редких явлений (выигрыш автомобиля по лотерейному билету, число рождения четверней, число несчастных случаев на производстве, число опечаток в большом тексте и т.д.). При этом считается, что события появляются независимо друг от друга с постоянной средней интенсивностью, характеризующейся параметром a=np.

Ряд распределения д.с.в.Х, имеющий распределение Пуассона, имеет вид:

X=k				…	k	…
P				…		…

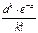
Контроль: Принимая во внимание разложение функции в степенной ряд и то, что х=а имеем: .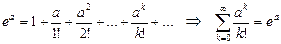

Тогда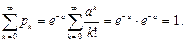

Числовые характеристики

· математическое ожидание:

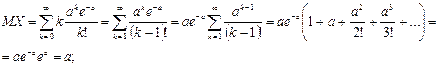
Итак, .

· дисперсия:

Итак, . Значит, .

Параметр а пуассоновского распределения равен одновременно м.о. и дисперсии с.в.Х, имеющей это распределение. В этом отличительная особенность изучаемого распределения, которая используется на практике (на основании опытных данных находят оценки для м.о. и дисперсии; если они близки между собой, то есть основание считать, что с.в. распределена по закону Пуассона).

Пример: Вероятность попадания в цель при одном выстреле равна 0,01. Составить закон распределения числа попаданий при 200 выстрелах. Найти м.о., дисперсию и с.к.о. числа попаданий. Какова вероятность того, что число попаданий составит не менее 5 и не более 10?

Дата добавления: 2014-01-07