Поверхні обертання

Поверхня обертання це поверхня, утворена обертанням даної просторової кривої γ навколо даної прямої l. Пряма називається віссю поверхні обертання.

Нехай: вісь обертання — це вісь Оz, а крива γ лежить в площині Оyz (x=0).

γ: .

Візьмемо будь-яку точку М₀(х₀,y₀,z₀) на кривій γ. 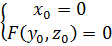. Cкладемо рівняння кола, яке вона описує при обертанні навколо осі Оz. Коло лежить в площині z =z₀ з центром в точці Р₀(0,0,z₀) і радіусом М₀Р₀, і М₀Р₀² =х₀² + y₀². Рівняння кола запишемо як перетин колового циліндра і площини

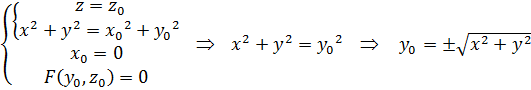Þ

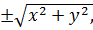F ( z)=0

F ₁(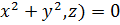

Отже, рівняння поверхні обертання з віссю Оz можна записати у такому вигляді:

G (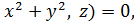тобто, змінні х, у входять в це рівняння не окремо, а групою 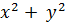. І навпаки, якщо рівняння має такий вигляд, то це рівняння поверхні обертання з віссю Оz (Подумати чому.).

Приклад. Впізнати і зобразити поверхню: 2(х²+у²)+3z=0. Це поверхня обертання з віссю Оz, бо змінні х,у входять групою х²+у². Перетнемо її площиною, що проходить через вісь Оz, наприклад площиною Оуz. Її рівняння х=0.

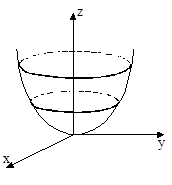Отримаємо рівняння кривої: 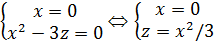– це парабола вітками вверх в площині Оуz. Намалюємо цю параболу. При обертанні навколо Оz отримаємо поверхню обертання (трошки пізніше ми дізнаємось її назву – коловий параболоїд).

Інші поверхні другого порядку.

Метод плоских перерізів дослідження поверхонь. Нехай є рівняння поверхні. Перетинаємо її площинами отримуємо деякі криві, які зображаємо в декартовій системі координат Охуz. Ці криві допоможуть уявити поверхню і намалювати її. Частіше використовують координатні площини та паралельні їм.

Еліпсоїд: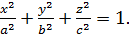

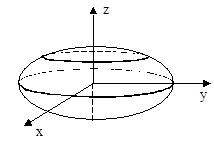Дослідимо поверхню методом плоских перерізів.

Перетнемо спочатку площиною Оху: z=0.

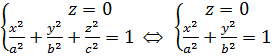-- еліпс з півосями а і b в площині Оху. Малюємо його.

Аналогічно, перетинаючи поверхню площинами Оуz та Охz, отримаємо еліпси з півосями відповідно b,c та a,c. Зображуємо їх.

Перетнемо площиною, паралельною до площини Оху: z=с. Отримаємо: 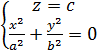-- одна точка, координатами (0,0,с).

Перетнемо ще площиною, паралельною до площини Оху: z=с/2. Отримаємо: 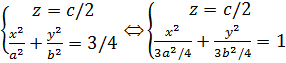-- еліпс з півосями 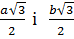(вужчий еліпс) в площині z=с/2. Отримали поверхню, подібну на яйце.

Частковий випадок: a=b=c=r.

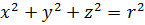– рівняння сфери з центром в початку координат з радіусом r.

Гіперболоїди: а) однопорожнинний

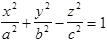-- рівняння однопорожнинного гіперболоїда (у рівнянні один мінус).

Перетнемо площиною Оуz. Лінія перетину визначається системою рівнянь: 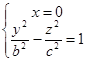-- маємо гіперболу з півосями b і с, причому дійсна вісь гіперболи співпадає з віссю O у.

Перетнемо площиною Оху. Отримаємо 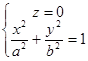-- рівняння еліпса з півосями а і b в площині Оху.

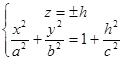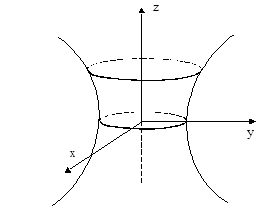
Розглянемо переріз поверхні площинами z=±h, паралельними до площини O ху. В перерізі одержуємо лінію, визначену системою рівнянь -- еліпс з півосями 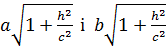(ширший еліпс) в площинах z= ±h. Отримали поверхню, зображену на малюнку.

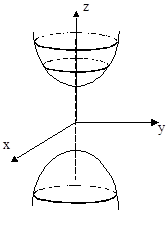
б) Двопорожнинний гіперболоїд:

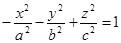-- рівняння двопорожнинного гіперболоїда (у рівнянні два мінуси).

Перетнемо площиною Оуz. Лінія перетину визначається системою рівнянь: 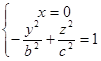-- маємо гіперболу з півосями b і с, причому дійсна вісь гіперболи співпадає з віссю Oz.

При z=0 отримаємо 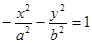. Отже, перетин з площиною Оху є Æ.

При z=±с отримаємо 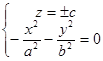-- точки М₁(0,0,с) і М₂(0,0,-с).

Розглянемо переріз поверхні площинами z=± 2 с, паралельними до площини O ху. В перерізі одержуємо лінію, визначену системою рівнянь 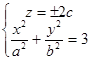-- еліпс з півосями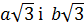

При більших |z| отримаємо ширші еліпси. Поверхня зображена на малюнку.

Параболоїди: а) еліптичний параболоїд

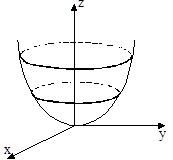
—рівняння еліптичного параболоїда;

Вправа. Переконатись методом плоских перерізів, що він має саме такий вигляд як на малюнку.

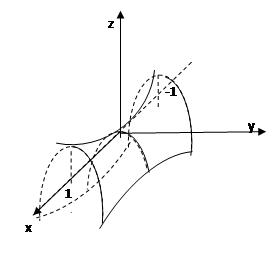
б) гіперболічний параболоїд

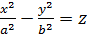— рівняння гіперболічного параболоїда.

В площині Oyz: х= 0 то 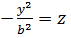– парабола вітками вниз.

В перерізі площинами x=± 1 одержуємо: x=± 1, 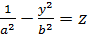– подібні параболи вітками вниз з вершинами, піднятими на висоту .

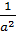В площині Oхz: у= 0 то 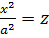– парабола вітками вверх. На цій параболі якраз розміщені вершини попередніх парабол. (Уявляємо поверхню, утворену рухом параболи (паралельної до площини Оyz) вітками вниз так, що її вершина на параболі вітками вверх в площині Охz.)

В площині z= -1 отирмуємо: z= -1, 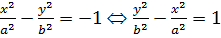— гіпербола, з дійсною віссю Оу. Отже, точки рухомої параболи на висоті z= -1 з’єднуються цією гіперболою.

Отримали поверхню подібну на сідло.

Дата добавления: 2014-01-07