Полярна система координат на площині

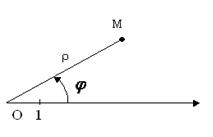Виберемо на площині деяку фіксовану точку О - початок координатної системи або полюс. Фіксований промінь (напівпряма) з вибраним на ньому одиничним відрізком з початком в полюсі назвемо полярною віссю.

Положення будь-якої точки М на площині будемо визначати впорядкованою парою чисел: довжиною r радіуса - вектора 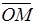та кутом j між полярною віссю і вектором 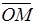. Кут вважається додатнім, якщо напрям обертання від полярної осі до радіус-вектора береться проти годинникової стрілки.

Числа r і j називаються полярними координатами точки М, М(r,j). Координати r і j повністю визначають положення точки М. Задання точки М однозначно визначає лише число r - довжину радіуса-вектора. Полярний кут визначається тільки з точністю до доданка, кратного 2p. Для полюса полярний кут взагалі не визначений. Довжина радіус-вектора r для різних точок площини може змінюватися від 0 до + ¥, полярний кут j від - ¥ до + ¥.

Як і в декартовій системі координат, кожній лінії на площині відповідає рівняння, яке зв`язує r і j, і, навпаки, кожному рівнянню, яке зв`язує r і j, відповідає, як правило, деяка лінія на площині із заданою полярною системою координат. Отже, F(r,j)=0 – рівняння лінії в полярній системі координат. Можна виразити змінну r. Отримаємо рівняння r=r(j).

Для побудови лінії, заданої рівнянням r=r(j) в полярній системі координат, частіше використовують метод побудови по точках, але спочатку доцільно знайти область зміни кута j, зважаючи на те, що відстань до початку координат r³0.

Розглянемо деякі лінії в полярній системі координат.

1. r=с, де с=сonst – коло з центром в полюсі з радіусом с (с³0).

2. j=с, де с=сonst – промінь, що виходить з початку координат під кутом с до полярної осі.

3. Побудувати лінію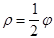

Область допустимих значень (ОДЗ): r³0, то j³0.

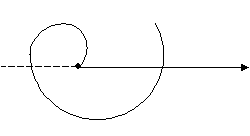
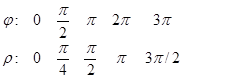
Одержана лінія називається спіраллю Архімеда.

4. Побудувати лінію r= а (1+cosj). (а = сonst, а ³0).

ОДЗ: r³0

1+cosj³0 Û cosj³-1 Û jÎℝ. Але достатньо побудувати для jÎ[0,2 π ], далі і напрямок буде повторюватись і r також, бо cosj має період 2 π.

Складаємо таблицю: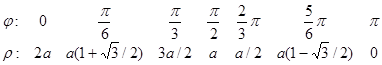

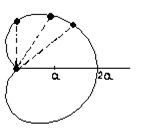Оскільки сosj=cos(2p-j), то обчислення значення r при p<j<2p не потрібно. Крива повинна бути симетричною відносно полярної осі. Наносячи відповідні точки на рисунок і сполучаючи їх плавною лінією, одержимо лінію. Ця лінія називається кардіоїдою.

Перехід від полярної системи координат до декартової і навпаки

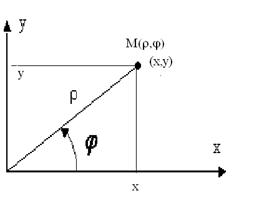
Помістимо початок декартової системи координат в полюсі полярної системи і направимо вісь абсцис вздовж полярної осі. Одиничні відрізки на осях Ох, Оу виберемо рівними одиничному відрізку на полярній осі.

Нехай точка М має координати (r,j) та (х,у) в полярній та декартовій системах відповідно. Тоді із співвідношень в прямокутному трикутнику: x=r×cosj, y=r×sinj.

Також знаходимо: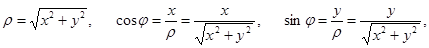tg j = .

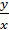j = arctg + πk, kÎℤ, k – парне, або непарне – вибирають так, щоб кут j був у потрібному квадранті.

Приклад. Зобразити криву r= a cosj (a >0). Потім перейти в рівнянні до декартової системи координат і впізнати криву.

ОДЗ: r³0

cosj³0 Û cosj³0 Û jÎ[-p/2+2pk, p/2+2pk], kÎℤ. Але достатньо побудувати для jÎ[-p/2, p/2], далі і напрямок буде повторюватись і r також, бо cosj має період 2p.

O a

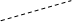
Складаємо таблицю: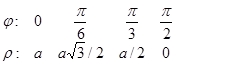

Оскільки сos(-j)=cosj, то обчислення значення r при -p/2<j<0 не потрібно. Крива повинна бути симетричною відносно полярної осі. Наносячи відповідні точки на рисунок і сполучаючи їх плавною лінією, одержимо лінію.

Перейдемо до декартової системи координат: 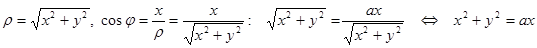-- рівняння кола. Знайдемо центр і радіус:

. Отже, це коло з центром в точці (a /2,0), з радіусом a /2. Малюнок це підтверджує.

Дата добавления: 2014-01-07