Пример 2.1.3 (ненасыщенного потока )

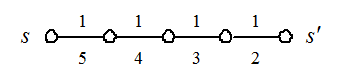
Рис. 2.2

Пусть из истока 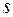в сток 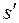пущен поток 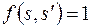. Тогда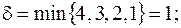

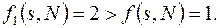
Пример 2.1.4. Пусть задана сеть, см. рис. 2.3. Построить максимальный поток и минимальное сечение.

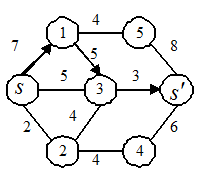
Рис. 2.3

Построим путь 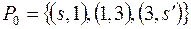. Множество вершин, образующих путь, обозначим через , см. рис. 2.3а). Очевидно, что 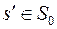. Следовательно, сечения нет. Пропустим вдоль пути 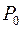поток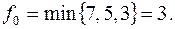

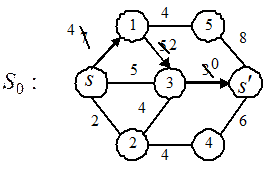
Рис. 2.3а)

,

Матрица пропускных способностей имеет вид, см. табл. 2.1.

Таблица 2.1

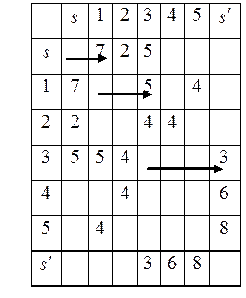
Аналогично продолжаем построения путей, ненасыщенных потоком , см. рис. 2.3б) – 2.3в).

Рис. 2.3б)

,

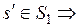
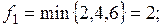
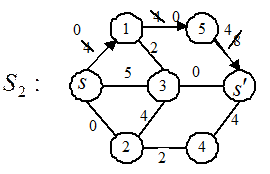
Рис. 2.3б)

,

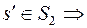
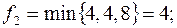
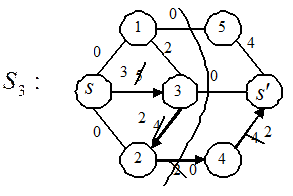
Рис. 2.3в)

,

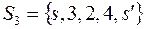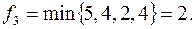
Поскольку больше путей, ненасыщенных потоком 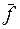построить не удается, то максимальный поток (сумма всех потоков из 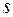в сеть) , а минимальное сечение где 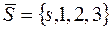, , см. рис. 2.3в).

Пример 2.1.5. Рассмотрим сеть 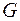, рис. 2.4. Цифры на ребрах – пропускная способность. Требуется найти максимальный поток и минимальное сечение.

Рис. 2.4

Составим матрицу пропускной способности 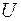(симметричная матрица), см. табл. 2.2.

Таблица 2.2

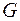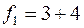Шаг 1. Пропустим по сети произвольный поток пускаем поток по вершинам 1, 3. Пропускаем также поток через вершину 4: . Мощность потока (сумма всех потоков из 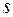в сеть).

Запишем матрицу 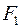для данного потока, см. табл. 2.3. 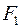– кососимметричная матрица: .

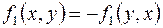Мощность потока можно также посчитать, как сумму элементов 1-й строки матрицы 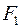. Сумма потоков из сети в 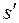равна мощности потоков, взятой с обратным знаком (сумма элементов последней строки). Для всех вершин, кроме 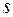и 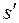, мощность потока в сеть равна нулю (сумма элементов соответствующей строки).

Найдем разность матриц 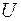и 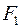и получим матрицу остаточной пропускной способности после прохождения потока , табл. 2.3.

Таблица 2.3

Найдем путь , ненасыщенный относительно потока . Пусть 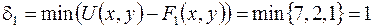. Пропускная способность ребра : .

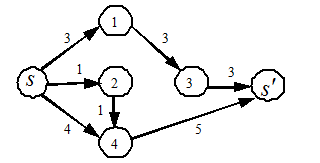
Рис. 2.4а)

Шаг 2. Аналогично строятся матрицы и 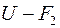, табл. 2.4. Найдем путь 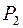, ненасыщенный относительно потока : , .

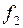Таблица 2.4

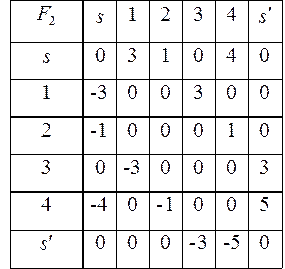
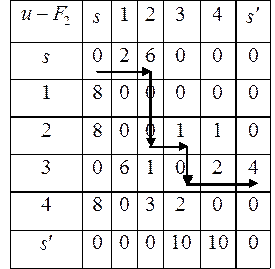
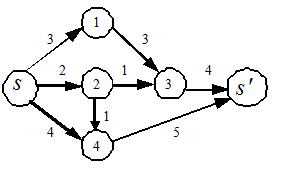
Рис. 2.4б)

Шаг 3. Строим матрицы и 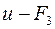, табл. 2.5. Мощность потока , , .

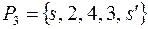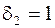Таблица 2.5

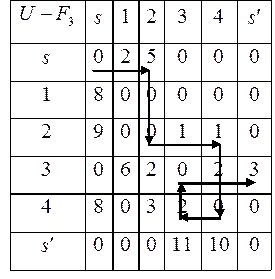
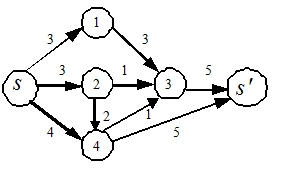
Рис. 2.4в)

Шаг 4. Строим поток 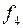мощности 1, табл. 2.6, добавляем к потоку .

Таблица 2.6

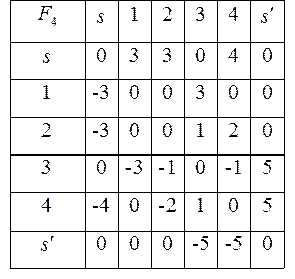
Так как больше на пути ничего не встречается, максимальный поток .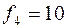

Дата добавления: 2014-01-07