
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Приклад 38
Написати рівняння площини, яка проходить через початок координат і через лінію перетину двох площин, заданих рівняннями x+y-5=0 і x-2z+1=0.
Розв'язання: Шукана площина належить пучку площин, які проходять через лінію перетину даних площин. Рівняння цього пучка площин має вигляд: α(x+y-5)+β(x-2z+1)=0, причому коефіцієнти α і β визначені з точністю до пропорційності. Так як початок координат повинен належати шуканій площині, то координати точки О задовольнятиму останнє рівняння. Отримаємо: -5α+β=0. Покладемо, наприклад, α=1, тоді β=5 і рівняння 6x+y-10z=0 є рівнянням шуканої площини.
4. Геометричний зміст знака Ах+Ву+Сz+D.
Нехай в афінній системі координат (0,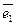 ,
,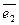
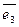 ) задано площину
) задано площину 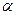 : Ах+Ву+Сz+D=0. Вона розділяє множину точок простору на два підпростори. Знайдемо умови, які визначають ці підпростори.
: Ах+Ву+Сz+D=0. Вона розділяє множину точок простору на два підпростори. Знайдемо умови, які визначають ці підпростори.
Зафіксуємо на площині 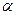 точку
точку 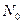 і відкладемо від неї нормальний вектор площини
і відкладемо від неї нормальний вектор площини 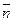 =(А,В,С) (рис.27). Кінець вектора позначимо N. Отже,
=(А,В,С) (рис.27). Кінець вектора позначимо N. Отже, 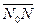 =
= .
.
Нехай M(x,y,z) довільна точка простору, яка не належить площині 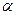 , Проведемо через М пряму d паралельну
, Проведемо через М пряму d паралельну
до вектора  , і отримаємо точку
, і отримаємо точку 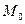 (
(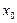 ,
, ,
,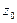 ) - точку перетину прямої d з
) - точку перетину прямої d з 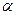 . Оскільки
. Оскільки  //
//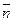 , то за теоремою 1
, то за теоремою 1  =
=
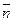 , або в координатах: х-
, або в координатах: х-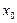 =
= A, y-
A, y- =
= B, z-
B, z-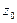 =
= C. Звідки х=
C. Звідки х= A+
A+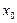 , у=
, у= B+
B+ , z=
, z= C+
C+ 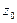 .Підставивши отримані змінні в многочлен Ax+By+Cz+D, отримаємо:
.Підставивши отримані змінні в многочлен Ax+By+Cz+D, отримаємо:
Ax+By+Cz+D=A( A+
A+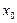 )+B(
)+B( B+
B+ )+C(
)+C( C+
C+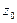 )+D=
)+D= (A2+B2+C2) (Так як точка
(A2+B2+C2) (Так як точка 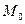 (
(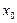 ,
, ,
,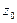 ) належить площині
) належить площині 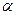 , то A
, то A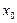 +B
+B +C
+C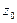 +D=0). Нехай
+D=0). Нехай 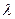 півпростір з границею
півпростір з границею 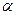 , який містить точку N. Тоді, із рівності
, який містить точку N. Тоді, із рівності  = =
= =
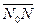 випливає, що точка М належить півпростору
випливає, що точка М належить півпростору 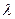 тоді і тільки тоді, коли
тоді і тільки тоді, коли  >0, а оскільки А2+В2+С2>0, то точка М належить півпростору
>0, а оскільки А2+В2+С2>0, то точка М належить півпростору 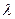 тоді і тільки тоді, коли Ах+Ву+Сz+D>0. Отже, нерівність Ax+By+Cz+D>0 визначає півпростір, обмежений площиною
тоді і тільки тоді, коли Ах+Ву+Сz+D>0. Отже, нерівність Ax+By+Cz+D>0 визначає півпростір, обмежений площиною 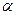 . Так як площина розділяє простір на два півпростори, то очевидно, що другий півпростір
. Так як площина розділяє простір на два півпростори, то очевидно, що другий півпростір 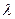 ' визначається нерівністю:Ax+By+Cz+D<0.
' визначається нерівністю:Ax+By+Cz+D<0.
|
|
Дата добавления: 2014-01-07; Просмотров: 443; Нарушение авторских прав?; Мы поможем в написании вашей работы!