Лекція 4. Тверді розчини – основна мінеральна форма знаходження хімічних елементів в природі

Механізм складається з двох рухомих ланок 2 і 3, що входять в обертальні пари 5-го класу А і В зі стояком 1 і вищу пару С 4-го класу, елементи ланок якої являють собою кола деяких радіусів.

Визначимо ступінь вільності даного механізму

w=3n-2P₅-P₄=3*2-2*2 - 1 = 1. (9)

Можна показати, що розглянутий механізм може бути замінений еквівалентним йому механізмом шарнірного чотириланковика (АО₂О₃В). Вища пара 4-го класу в точці С замінюється ланкою 4, щовходить у точка х О₂ і О₃ в обертальні пари 5 класу. Отриманий у результаті заміни механіз м (АО₂О₃В) еквівалентний вихідному. Ступінь вільності W механізму, що отримали, буде такий, що й у заданого механізму. Маєм о

w=3n-2P₅=3*3-2*4 = 1. (10)

Розглянутий спосіб отримання еквівалентного механізму, можна узагальнити. Нехай заданий механізм із вищою парою, елементи ланок якої являють собою довільно задані криві (а) і (в) (рис.2).

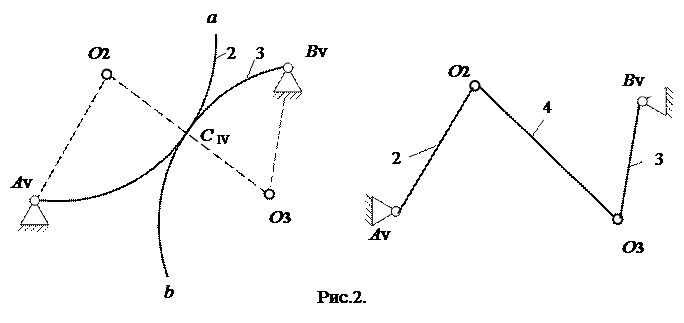
Для побудови схеми еквівалентного механізму, проведемо нормаль n-n у точці С дотику кривих і відзначаємо на ній центри О₂ і О₃ кривизни кривих (а) і (в). Як і раніше центри кривин и О₂ і О₃ ми вважаємо шарнірами, що утворюють обертальні пари.

Описана заміна правильна для заданого положення основного механізму. В іншому положенні схема еквівалентного механізму, залишиться тією ж, але розміри його ланок зміняться, тому що центрикривини О₂ і О₃ змістяться.

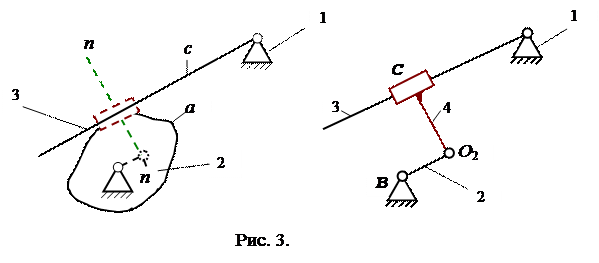Якщо один з дотичних елементів буде являти собою деяку криву, а другий - пряму (рис.3), то центр кривизни другого профілю буде знаходитись нескінченно далеко.

Умовна ланка 4 у цьому випадку буде входити в центрі кривизни О₂ ділянки дотику ланки 2 в обертальну пару 5-го класу. Друга обертальна пара, в яку повинна входити ланка 3 має вісь обертання нескінченно далеко і тому переходить у поступальну пару також 5-го класу.

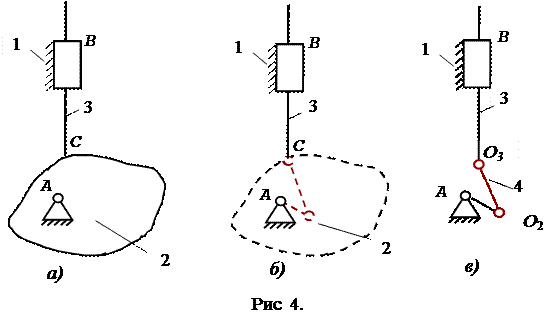Далі розглянемо випадок коли один з елементів пари крива (ланка 2), а інший – точка (ланка 3) (рис.4).

У цьому випадку центр кривини О₃ збігається із самою точкою С і тому умовна ланка 4 мусить входити в дві обертальні пари 5-го класу - з віссю, що проходить через центр кривини О₂ криволінійного елемента (а) і в обертальну пару з віссю, що проходить через точку С.

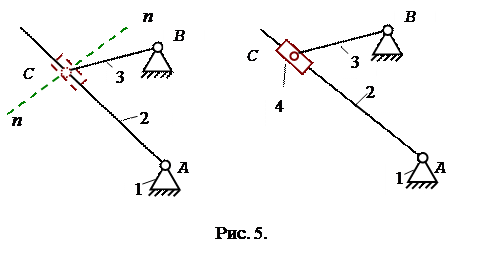Розглянемо ще один випадок, коли одним елементом є пряма АС, а

іншим – точка С (рис.5).

У цьому випадку заміна зводиться до постановки умовної ланки 4, що входить в одну поступальну й одну обертальну пари. Вісь обертальної пари і вісь руху поступальної пари повинні проходити через точку дотику С.

Розглянемо далі випадок, коли обертальний рух передається за допомогою зубчастого евольвентного зачеплення (рис.6).

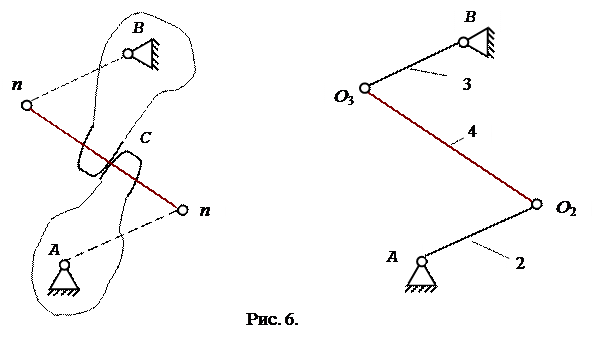У цьому випадку аналогічно на загальній нормалі n-n визначаємо центри кривизни, які з'єднуємо додатковою ланкою

Так, будь-який плоский механізм із вищими парами 4-го класу може бути замінений механізмом, до складу якого входять тільки нижчі кінематичні пари 5-го класу. Рекомендується наступна перевірка правильності виконаної заміни: у результаті заміни замість однієї кінематичної пари 4-го класу з'являються дві пари 5-го класу і додаткова умовна ланка. Ступінь рухомості механізму, що замінює, повинен бути рівним ступеню рухомості вихідного механізму.

Розчини термодинамічно вигідні. Якщо ми згадаємо рівняння вільної енергії Ґібса G=H-TS, а також визначення ентропії S як міри впорядкованості системи, тоді зможемо зробити висновок, що збільшення кількості сортів атомів, що приймають участь у будові речовини призводить до збільшення ентропії системи. Так як ентропія входить у рівняння із від’ємним знаком, значить її збільшення спричинює зменшення вільної енергії Ґібса.

Якщо у нас є дві речовини, то із ними ми можемо зробити дві операції:

1. Змішати їх утворивши механічну суміш; при цьому хімічна взаємодія між речовинами не відбувається.

2. Змішати із взаємним розчиненням. При розчиненні відбувається хімічна взаємодія, що проявляється в зміні вільної енергії системи і виділенні або поглинанні тепла.

Розчинення – це реакція, що може бути екзотермічною або ендотермічною. Так взаємне розчинення спирту і води відбувається із виділенням тепла – екзотермічно, а розчинення нітрату амонію у воді із поглинанням тепла – ендотермічно. Інтенсивне швидке розчинення NaNO₃ в H₂O може призвести до замерзання розчину, тоді як таке ж розчинення H₂SO₄ в H₂O може викликати кипіння розчину.

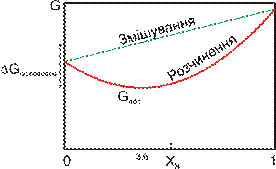
Рис. 6.1. Схема, що ілюструє енергетичну відмінність між утворенням механічної суміші двох речовин і їх розчиненням. Зміна вільної енергії системи при змішуванні лінійна, пропорційна частці компонента B (XB) в суміші. Вільна енергія розчину при всіх значеннях XB є меншою енергії механічної суміші. Різниця між ними складає енергію розчинення (ΔG) сполук A і B. Максимальне виділення енергії відповідає мінімуму вільної енергії розчину і певному значенню XB (в даному випадку ~ 3.6), що відповідає стехіометрії мінералу-твердого розчину.

Із рис. 6.1 ми бачимо, що розчинення є енергетично вигідним. Якщо ж звернемося до рівняння вільної енергії, то ми бачимо, що збільшення температури призводить до збільшення вкладу ентропії у зменшення енергії. Відповідно, збільшення температури призводить до зростання ролі розчинів у геохімічних системах.

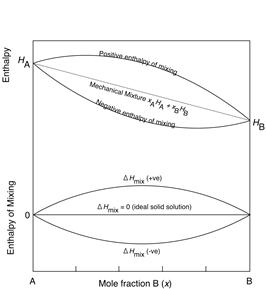
Поряд із цим, хімічні взаємодії в ході розчинення супроводжуються зміною хімічних зв’язків в системі, тобто зміною внутрішньої енергії системи. На рис. 6.2 показана можлива зміна ентальпії системи при розчиненні, порівняно із формуванням механічної суміші.

Якщо між двома речовинами не відбувається хімічна взаємодія, то сумарна ентальпії системи наближається до ентальпії механічної суміші. Зменшення вільної енергії системи досягається тільки за рахунок зростання ентропії. Такі розчини називаються ідеальними.

У більшості геохімічних систем між компонентами, що формують розчин, відбувається хімічна взаємодія, що супроводжується зменшенням або збільшенням ентропії розчину (на рисунку ми бачимо криві, що відповідають позитивній чи негативній ентальпії розчинення). Такі розчини називаються реальними.

В ідеальних розчинах взаємодіючі кількості сполук відповідають їх концентрації в суміші, тоді як в реальних розчинах, внаслідок взаємодії між атомами, молекулами та іонами, взаємодіючі кількості відрізняються від концентрації, переважно в сторону зменшення. Тому, описуючи взаємодії в реальних розчинах, ми повинні користуватися поняттям активності компонента, що пов’язана із концентрацією виразом

,

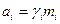де a_i – активність компонента i, m_i – моляльна концентрація компонента i, γ _i – коефіцієнт активності компонента i.

Ентропія і ентальпії здійснюють протилежний вплив на вільну енергію системи. Якщо в ході змішування ентальпія зростає, а її приріст буде перевищувати приріст ентропії і результуюча вільна енергія буде зростати ­ розчин не буде утворюватися.

Якщо при змішуванні ентальпія розчину зменшується, або її приріст є меншим за приріст ентропії, то вільна енергія системи буде зменшуватися і розчин буде стабільним.

Так як ентальпія та ентропія залежать від температури, то зміна ентальпії та ентропії розчинення із температурою є важливими факторами, що контролюють стабільність розчинів. Із збільшенням температури частка ентропії у вільній енергії системи зростає і розчини будуть формуватися навіть при позитивній ентальпії розчинення. Підтвердженням цього є повсякденні спостереження росту розчинення речовин у гарячій воді. Зниження температури веде до зниження розчинності і випадіння із розчину кристалів розчиненої речовини.

А

Б

В

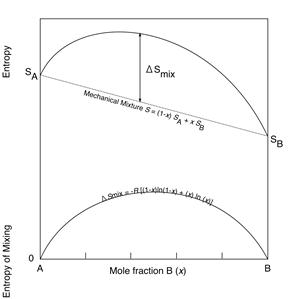
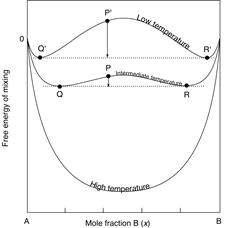
Рис. 5.2. Зміна ентропії та ентальпії при розчи­нен­ні двох сполук А і В. Показані криві ентропії та ентропії розчину в порівнянні із лінійною зміною параметрів механічної суміші та зміна ентро­пії та ентальпії розчинення. На рис. В показана зміна вільної енергії розчину із позитивним приростом ентальпії розчинення при зменшенні температури. При високій температурі розчин є стабільним у всьому інтервалі змішування, а при низькій існують два розчини: розчин незначної кількості B в сполуці A та розчин незначної кількості A в сполуці B.

Компонент, який переважає в розчині називається розчинником, а компонент що міститься у меншій кількості називається розчиненим. Якщо в системі при змішуванні існує тільки один мінімум вільної енергії, то розчинник і розчинений компонент будуть змінюватися місцями із зміною X_B.

За речовинним станом виділяють два типи розчинів:

1. рідкі розчини, в яких розчинник знаходиться в рідкому стані. В геохімічних системах такими розчинами є

a. водний розчин – розчинник вода, розчиненими компонентами є та аніони, комплексні аніони, нейтральні молекули;

b. магма – розчинником є алюмосилікатний розплав в якому розчинені оксиди мета­лів, вода, гази;

c. нафта – складний вуглеводневий розчинник, в якому розчинені різноманітні рід­кі та тверді вуглеводні, гази, вода та мінеральні речовини та метали.

2. Тверді (кристалічні) розчини – тверді кристалічні тіла, що мають однорідну струк­ту­ру, в якій певні еквівалентні позиції можуть бути зайняті різними іонами (атомами, комплексами) без істотної зміни симетрії структури в цілому.

Розглянемо спочатку природу і особливості формування твердих розчинів.

Дата добавления: 2014-01-07