
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Метод однородных функций и метод моделирования для восстановления геологического разреза в Тибете по данным преломленных волн
|
|
|
|
В.Б. Пийп, Е.А. Ефимова
Новые структуры региона получены в результате интерпретации первых вступлений сейсмических преломленных волн по профилю INDEPH III в Центральном Тибете.
Метод обращения есть численное обобщение формулы Герглотца-Вихерта на случай 2-мерно неоднородной среды – метод однородных функций.
Новый разрез показывает, что сутура BNS представляет собой сложный контакт в верхней коре, а в средней коре ее продолжает листрический надвиг, выполаживающийся на кровле нижней коры, которая приподнята в северной части разреза до глубины 32 км. Ниже кровли средней коры прослеживается слой с пониженной скоростью волн. Средняя кора деформирована и образует наклонные листрические надвиги в южном направлении. В верхней коре южнее BNS выделяются области с повышенной скоростью и градиентом скорости, это, видимо, области развития магматизма. Севернее BNS в верхней коре различаются спокойные очертания структур. Использованные нами входные данные были интерпретированы ранее международным коллективом авторов методом моделирования. Результаты сравниваются и различия объясняются.
Ключевые слова: Глубинное сейсмическое зондирование, обратные задачи, Тибет, метод моделирования, метод однородных функций
Введение. Интерпретация данных ГСЗ имеет определенные проблемы. Обычно применяются следующие методы: лучевое трассирование (моделирование) или методы томографии, при этом каждый из этих методов, нуждается в начальной модели, которая обычно производится одномерной инверсией. Техника лучевого трассирования требует экстремально большого времени. Для использования томографии требуется чрезвычайно плотная система наблюдений. Результативный разрез при этом оказывается бедным и гладким без каких-либо скоростных (геологических) границ. Вдобавок оба метода испытывают трудности при восстановлении сред с волноводами. Метод моделирования требует, чтобы каждый сегмент годографов был предварительно отнесен к какому-либо слою или границе раздела. А это очень трудная и неоднозначная проблема для интерпретатора. Присутствие в разрезе волноводов – это не исключительный случай. Волноводы существуют внутри каждого разреза на фоне общего увеличения скорости с глубиной. Об этом свидетельствуют многочисленные данные акустического каротажа скважин.
Метод однородных функций во многих отношениях свободен от проблем, связанных с низкоскоростными слоями (волноводами). Сейсмический профиль в центральном Тибете это пример интерпретации данных в сложных неоднородных средах с волноводами. Данные взяты из Zhao et al. (2001).
Геологическое строение. Субмеридиональный профиль INDEPH III пересекает сложный геологический шов между полуостровом Индостан и Гималаями в районе Тибета (рис. 5.1). По геологическим представлениям полуостров Индостан был причленен к структурам южной Азии в Четвертичном периоде коллизией между блоками Лхаса и Киангтанг и последующей коллизией с южной Азией (Allegre et al., 1984). Вдобавок мы показали, что главные черты нашего разреза находят отражение в наблюденном временном поле, т.е. в разрезе офсетов.
Метод инверсии. Метод однородных функций (Piip, 2001) - это решение обратной задачи для двухмерно-неоднородных сред методом простой инверсии.
Геологические среды очень сложны. Это трехмерные многослойные среды с криволинейными поверхностями раздела и множеством субвертикальных поверхностей разрыва – тектонических нарушений. Следовательно, мы должны использовать подходящие модели для аппроксимации сейсмических сред. Преобладающей чертой геологических разрезов можно считать подобие геологических границ. Достаточно представить себе синклинальные, антиклинальные и другие складки. Изолинии скорости однородных функций 2-х координат это кривые подобные друг другу, форма кривых может быть произвольной. Однородные функции 2-х координат не имеют ограничений в отношении величин вертикальной и горизонтальной составляющих градиента скорости и могут содержать прямолинейные наклонные линии разрыва скорости – границы раздела. Однородные функции это широкий класс бесконечномерных функций. По этим причинам однородные функции очень удобны для сейсмической аппроксимации геологических сред и интерпретации сейсмических данных. Метод однородных функций автоматически обращает годографы первых вступлений в двухмерное скоростное распределение, которое включает границы раздела.
Метод обобщает классические методы решения обратных кинематических задач сейсмики на случай двухмерно-неоднородных сред. Методы томографии и методы лучевого моделирования не относятся к классическим обратным задачам. Эти методы решают обратную задачу путем многократного решения прямой задачи, что обусловливает непомерно большое время, требуемое для такого решения, помимо других трудностей.
Классические методы решения обратной задачи это метод t0 для преломленных волн, методы определения эффективной скорости по годографам отраженных волн (постоянной разности, квадратичных координат и др.), а также метод обращения годографа рефрагированной волны – формула Герглотца-Вихерта-Чибисова. Все классические методы обращения разработаны для одномерных скоростных зависимостей. Модели однородно-слоистых сред, для которых созданы традиционные методы интерпретации, представимы как функции одной координаты – полярного угла. Более сложные разрезы получаются в результате локального применения исходных моделей.
Программный пакет ГОДОГРАФ для обработки, интерпретации и построения сейсмических разрезов по данным преломленных волн производит локальную аппроксимацию разреза непрерывными монотонно возрастающими с увеличением полярного угла 2D однородными функциями. Из рассмотрения алгоритма видно, что построение локального приближения скоростного поля, в сущности, является обобщением метода Герглотца-Вихерта-Чибисова на случай двухмерно-неоднородных сред. Теория наиболее подробно изложена в (Пийп, 1984; Пийп, 1991; Piip 2001).
 |
Алгоритм состоит в следующем. Для каждой пары встречных годографов, увязанных во взаимных точках, вычисляется аппроксимация реального разреза однородной функцией 2-х координат в области, куда проникают сейсмические лучи. В полярных координатах аппроксимирующая функция имеет вид
где действительное число m - степень однородной функции, ψ(φ) - произвольная возрастающая функция полярного угла и r >0. Так как ψ(φ) - произвольная функция, скоростная функция (1) является бесконечномерной. Функция (1) в декартовых координатах имеет вид
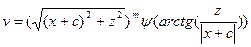 | |||
 | |||
Неизвестными здесь являются: m - степень однородной функции - действительное число, с – параметр, определяющий положение начала координат (полюса) на профиле, и функция ψ. Неизвестна также область среды, куда проникают сейсмические лучи, отвечающие паре встречных годографов.
Для нахождения значений m и с используется следующее свойство встречных годографов для среды (1), сформулированное в (Piip, 2001). Точки обратного наблюденного годографа с помощью простых преобразований непрерывно и однозначно отображаются в точки прямого годографа. Неизвестные параметры m и с находятся с помощью минимизации среднеквадратического отклонения прямого годографа от преобразованного в него встречного перебором искомых параметров. Наблюденные прямой и преобразованный в него обратный годографы совмещаются и осредняются некоторым «среднеарифметическим» годографом. Это, по существу, является сглаживанием наблюденных годографов. Так как для двух встречных годографов вычисляется единый «среднеарифметический» годограф, то автоматически производится отождествление точек встречных годографов, а значит и их особенностей для одноименных границ раздела. До настоящего времени, такую процедуру можно было осуществить только с использованием интерактивных систем интерпретации.
Далее мы ищем возрастающую функцию полярного угла по единственному «среднеарифметическому» годографу. Таким образом, двухмерная обратная задача сводится к одномерной задаче. Так же как и для случая возрастающей зависимости скорости от глубины, годограф для искомой возрастающей функции полярного угла является выпуклым (Piip, 2001). Мы не применяем произвольное сглаживание годографа выпуклой кривой, а выбираем среди множества точек «среднеарифметического» годографа некоторое подмножество его точек, лежащее на выпуклой ломаной. Это второй этап сглаживания, который используется при вычислении локальной скоростной зависимости. Таким образом, рассматриваемая нами задача в некоторой степени аналогична задаче Герглотца-Вихерта-Чибисова.
По найденному выпуклому годографу неизвестная функция полярного угла вычисляется численными методами как возрастающая ступенчатая функция. При этом используются формулы, справедливые для головных волн. Одновременно вычисляется семейство лучей. Это семейство лучей, вычисленное в предположении, что искомая функция полярного угла непрерывно возрастает, является регулярным, т.е. близкие лучи не пересекаются между собой. Это показано в работе (Piip, 2001). Для двух встречных годографов лучи заполняют область среды, ограниченную лучом, проходящим через точки источников. При этом точки поворота лучей располагаются, как показано на 4.21. Значения скорости вычисляются в точках поворота лучей. Точки поворота лучей концентрируются в нижней части локального скоростного поля. Это означает, что нижняя часть поля скорости определяется наиболее точно. Луч, проходящий через источники, ограничивает область, для которой найдена аппроксимация реального скоростного распределения однородной функцией 2х координат – локальное поле скорости.
Если интерпретируется сложная система наблюденных годографов, то для каждой пары встречных годографов, выбранной из системы годографов, независимо друг от друга вычисляется аппроксимация реального разреза некоторой однородной функцией (1). В результате вычисляется множество функций, количество которых всегда равно количеству пар встречных годографов. Этим самым автоматически устанавливается соответствие между детальностью скоростного поля и геометрией системы наблюдений. Таким образом, не нужны специальные тесты для проверки такого соответствия, как это делается в случае методов математического моделирования (Zelt, 1992).
Так как мы используем осреднение вычисляемого годографа выпуклой кривой, волновод внутри любого локального скоростного поля, если он существует, вместе с его высокоскоростной кровлей автоматически заменяется слоем с практически постоянной скоростью. Протяженные слои с низкой скоростью могут существовать только на границах локальных скоростных полей. Различные локальные скоростные поля для близких годографов мало отличаются друг от друга в областях, где они перекрываются. Это обусловлено тем, что обратная задача на множестве однородных функций имеет устойчивое решение (Пийп, 1984). Скоростные отклонения в точках разреза, полученные для различных близких пар встречных годографов, составляют погрешность аппроксимации.
Интерпретация, таким образом, включает два главных этапа: строгое решение обратной задачи, которое состоит в определении увеличивающейся однородной функции двух координат по двум встречным годографам первых вступлений и суперпозиции скоростных функций, вычисленных для различных пар встречных годографов. Результат этой суперпозиции оставляет только нижние (наиболее точные) части локальных скоростных полей в скоростном поле, Верхние части скрыты перекрывающим скоростным полем с более коротким расстоянием между источниками (рис. 4.22). Такая процедура фактически аналогична зрительному восприятию пространства. Человек, рассматривая удаленные предметы, фокусирует на них взгляд и не видит близко расположенные предметы. Человеческое зрение не способно видеть всю глубину пространства одновременно.
Чтобы визуализировать глубинный скоростной разрез после того, как определены все скоростные функции, можно применять различные способы. Можно, например, вычислять каждую изолинию скорости отдельно для наперед заданного значения скорости. Удобно, для визуализации разреза использовать многочисленные современные программные комплексы, предназначенные для работы с картами. Двухмерно-неоднородный разрез в математическом смысле является поверхностью. Следовательно, окончательный скоростной разрез может быть представлен скоростными значениями, вычисленными в точках прямоугольной сетки (грид презентация). Таким образом, представление разреза в виде сетки (грид) используется на конечном этапе только для того, чтобы визуализировать уже вычисленный разрез, и размер грид, который мы задаем, определяет только форму визуализации разреза.
Разрывы первого порядка для случая грид презентации выглядят подобно переходной зоне – протяженному региону сгущения скоростных изолиний, чья мощность равна размеру соответствующей сетки. Разрыв (граница) 2-го порядка в этом представлении есть линия, где резко изменяется величина градиента скорости. Инверсионные границы раздела, на которых скорость уменьшается сверху вниз, также определяются методом однородных функций Они тоже изображаются переходной зоной, мощность которой определяется размером ячейки.
При визуализации скоростного разреза параметры сетки не могут быть выбраны произвольно, так как при очень маленьком шаге сетки, будут видны границы локальных скоростных полей, а при очень крупном шаге не будут прослеживаться границы раздела и другие особенности скоростного поля. Таким образом, размер сетки определяет разрешенность разреза.
Для применения метода однородных функций могут быть использованы все типы волн, в том числе и отраженные волны, как это сделано в работе (Piip, 1984), однако, автоматический пакет «Годограф» в его настоящем виде использует только первые волны. При вычислении разреза мы не можем и не должны использовать никакую априорную информацию, так же как в случае применения формулы Герглотца-Вихерта-Чибисова, так как это обратная задача,
Чтобы выделить особенности глубинного скоростного разреза, можно использовать различные трансформации окончательного скоростного поля (градиент, составляющие градиента и т. д.).
Применяется интерполяция исходных данных – годографов первых вступлений в отношении приемников и источников. Непосредственно годографы трудно интерполировать, так как они зависят друг от друга. Мы интерполируем не годографы, а разрез равных удалений - это те же годографы, представленные в других координатах. При построении разреза равных удалений предварительно каждый годограф линейно и равномерно интерполируется в отношении приемников. Затем каждое интерполированное значение времени рассматривается как время во взаимной точке, и это значение относится к середине интервала источник-приемник. Таким образом, взаимные точки изображаются одной точкой. Полученное временное поле является однозначным и непрерывным и легко интерполируется, по этому полю можно восстановить годографы с источником в любой точке профиля. Так как для каждой пары встречных годографов мы можем вычислить только возрастающую функцию, использование только наблюденных годографов в случае слабой системы годографов, как в случае INDEPTH III, приведет к пропуску волноводов. Если система годографов достаточно полная или нет выраженных во временном поле волноводов, интерполяция не используется. Формулы интерполяции, которые мы используем, предложены Пузыревым Н.Н. в 1963 г. (Пузырев 1963) Это линейная интерполяция. Интерполяция всегда используется в сейсморазведке при построении любых сейсмических разрезов, так как наблюдения дискретны, а получаемые нами разрезы непрерывны. Ничего исключительного нет и в линейной интерполяции наблюденных времен, как в отношении приемников, так и в отношении источников, так как по принципу взаимности источник и приемник всегда можно поменять местами. Линейная равномерная интерполяция является сглаживающей процедурой и не вносит искажений в наблюденное временное поле. Параметры интерполяции выбираются по таким же принципам, как и в случае разрезов, полученных методом ОГТ - это хорошая прослеживаемость границ раздела и разломов, хороший контраст скоростей, решение геологической задачи. Использование сверх детальной интерполяции для достаточно полных систем наблюдений не приводит к улучшению разрешенности разреза, а наоборот приводит к увеличению шума (некоррелируемой изменчивости скоростного разреза).
Временной разрез равных удалений является изображением наблюденных годографов в специальных координатах. Главные особенности реального глубинного разреза отображаются во временном разрезе равных удалений. Это показано в Piip, 2001 с помощью модельных расчетов и скважинных данных. Временной разрез равных удалений позволяет увидеть, имеют ли отображение в наблюденном временном поле главные особенности вычисленного глубинного скоростного разреза.
Для демонстрации достоверности скоростных разрезов, полученных методом однородных функций, многократно рассчитывались теоретические годографы, которые всегда достаточно хорошо совпадают с наблюденными. Среднеквадратические отклонения лежат в пределах допустимых значений, принятых при оценке разрезов в современной интерпретации. При использовании метода однородных функций решение прямой задачи, вообще говоря, не требуется и применяется только для оценки окончательного глубинного разреза.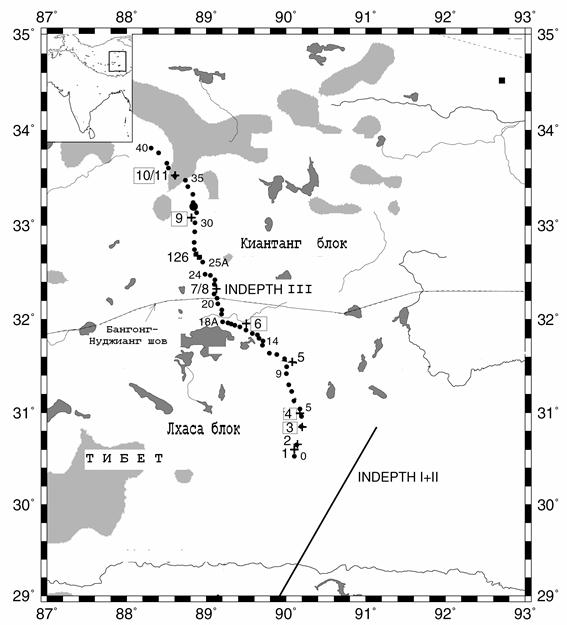
Рис. 5.1
Перентерпретация данных в центральном Тибете. Данные, относящиеся к 5 большим взрывам из 11, произведенных на INDEPTH III, приведены в Zhao et al. (2001). Если данные, относящиеся к трем крайним взрывам, исключить из рассмотрения, тогда только записи из 3 взрывов могут рассматриваться как пропущенные в этой работе. Записи, использованные нами, могут рассматриваться как наиболее информативные, как указывают Zhao et al. (2001).
Наша переобработка касается времен первых вступлений, которые Zhao et al. (2001) идентифицировали на записях и отметили крестиками. (рис 5.2). Мы не пикировали первые вступления на записях кроме тех, которые выделены Zhao и его соавторами. Первые вступления от Мохо не были записаны авторами, поэтому мы не произвели эту границу на новом разрезе. Незначительные ошибки, возникшие при оцифровке, оцениваются по невязкам времен во взаимных точках как 0.1 с, что лежит в пределах погрешности указанной в Zhao et al. (2001, таблицa 3)
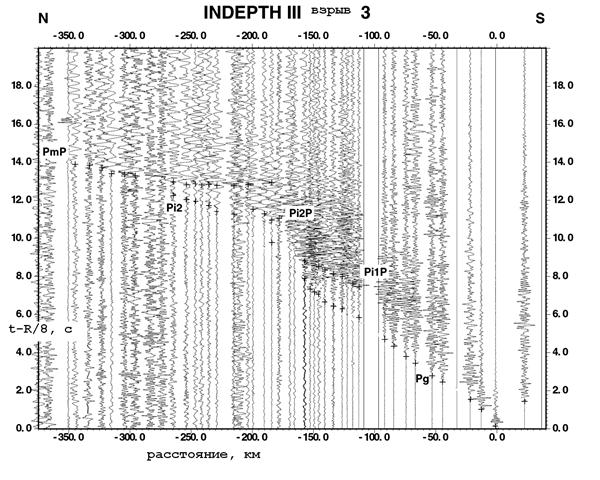
Рис.5.2
Наблюденные годографы - это ломаная линия с вершинами в точках, где зарегистрированы времена первых вступлений (пики) (рис. 5.3). Мы представляем годограф как непрерывную линию, а не как отдельные пики. Это связано с тем, что алгоритм является автоматическим и предусматривает вычисление производных. При таком представлении годографов зоны тени проявляются как участки с пониженной кажущейся скоростью. Такие же участки могут существовать на годографах и в случае существования в разрезе вертикальных блоков с пониженной скоростью. Эти случаи разделяются автоматически при вычислении скоростного разреза в случае достаточной системы наблюдений (более чем два встречных годографа).
Мы произвели линейную интерполяцию наблюденных годографов в отношении приемников с шагом 4 км. Мы используем наблюденное временное поле (поле изолиний равных удалений источник-приемник с шагом между изолиниями 4 км) для интерполяции годографов между источниками. Были вычислены годографы с источниками, расположенными с постоянным шагом 12 км (рис. 5.4). Эти годографы использованы для обращения методом однородных функций.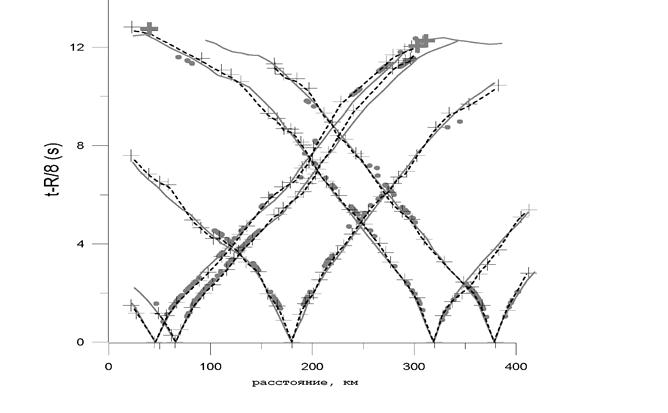
Рис. 5.3
Наблюденный временной разрез. Временной разрез с редукцией 8 км/с изображен на рис. 5.4 с осью времен, направленной вниз. Плотность изолиний пропорциональна кажущейся скорости. Области с высокой плотностью изолиний соответствуют областям с высокой кажущейся скоростью и области с низкой плотностью изолиний отвечат областям с низкой кажущейся скоростью. Линии изменения плотности изолиний могут рассматриваться как границы раздела слоев. мы выделяем эти черты на качественном уровне и только для сравнения с окончательным глубинным разрезом.
Следующие слои и зоны могут быть качественно выделены на наблюденном временном поле. На временах ниже 2 – 3 с, изолинии свидетельствуют о присутствии скоростных слоев с ненарушенной субгоризонтальной слоистостью. К югу от BNS крупная область с повышенной кажущейся скоростью прослеживается на временах 2 – 5 с, а к северу от BNS мощность этой области уменьшается и она трассируется приблизительно на временах 4 – 5 с. ля Кровля средней коры ограничивает эту область снизу. Мощная область с низкой кажущейся скоростью следится на временах от 5 до 8 с. Шов BNS трассируется в средней коре приблизительно на временах от 5 до 11 с. Он отделяет область с уменьшенной скоростью на юге от области с относительно высокой скоростью в северной части разреза. Несколько границ может быть выделено на временах от 8 до 11 с. Вблизи кровли нижней коры небольшой волновод прослеживается. Нижняя кора выделяется на временах около 11 с как область с высокой плотностью изолиний (рис. 5.4)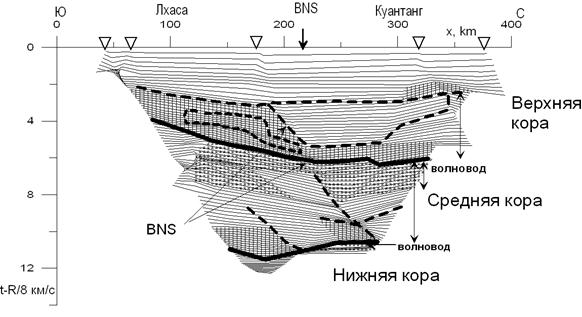
.
Рис. 5.4

Рис. 5.5
Глубинный разрез. Когда вычисляется глубинный разрез наблюденные времена предварительно не сопоставляются с какими либо слоями. Окончательный глубинный разрез - результат обращения годографов методом однородных функций - с геологической интерпретацией (границы и разломы) показан на рис. 5.6. Глубинный разрез представлен скоростными значениями на регулярной сетке размером 151 x 101 с 2.5 x 0.6 km ячейками. На глубинном разрезе, который мы произвели, резкие разрывы заменены переходными зонами, чья мощность равна размеру ячейки. Чтобы выделить границы раздела на этом разрезе мы использовали визуализацию глубинного разреза как поверхности с освещенным рельефом. На этом рисунке отчетливо видны границы раздела и разломы. Максимальное освещение (светлые линии) соответствует переходным зонам, где скорость резко возрастает с глубиной, минимальное (темные линии) инверсионным границам раздела (кровлям волноводов небольшой мощности).
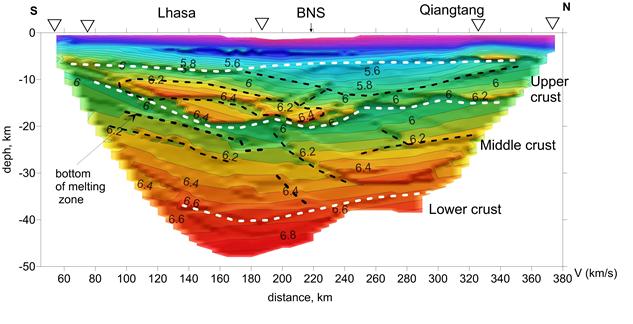
Рис.5.6
Протяженные границы раздела и разломы в новом глубинном разрезе превышают разрешение модели (2.5 х 0.6 км), они четко видны на разрезе, представленном как поверхность с освещенным рельефом и практически однозначно сопоставляются с границами раздела и разломами, которые видны в наблюденном временном поле равных удалений (на рис. 5.4).
Геологическая интерпретация нового разреза. Новый разрез для профиля INDEPTH III с геологической интерпретацией приведен на рис. 5.6.
Высокоградиентный осадочный слой располагается в верхней части разреза. В районе блока Лхаса его мощность составляет около 7 км, в районе
Киангтанг 5 км. Резкая инверсионная граница км отделяет осадочный слой от кровли консолидированной коры. Кровля консолидированной коры практически располагается на глубинах 5-7 км Сложный структурный раздел BNS (Бангонг-Нужианг шов) отделяет верхнюю кору блока Лхаса от верхней коры блока Киангтанг. Верхняя кора террейна Лхаса в новом разрезе содержит два субгоризонтальных слоя на глубине 7 -18 км и имеет повышенную скорость (6.4 км/с вблизи подошвы). Эти слои могут относится к изверженным породам, которые залегают в этой области, как известно из геологических данных. Верхняя консолидированная кора Киангтанг блока также разделяется на два слоя с относительно низкой скоростью и скоростным градиентом. Верхний слой образует хорошо выраженную депрессию до глубины 12 км.
Кровля средней коры - это криволинейная кровля слоя с пониженной скоростью, выделенная на глубинах 15-20 км мощностью около 5 км. Скорость падает от 6.2 до 5. км/с на кровле слоя. Мощность слоя с низкой скоростью переменна и увеличивается с севера на юг от значений 3 до 9 км. Относительно существования волновода в работе Zhao et al (2001) утверждается, что не имеется очевидных свидетельств существования среднекорового волновода в данных продольных волн, хотя эти данные не противоречат существованию такого слоя. Наши результаты отчетливо говорят о существовании волновода и хорошо согласуются с данными Zhi Min and Wu, (1987), где указывается, что в районе структурного шва BNS в Тибете интерпретация P и S волн приводит к выводу о существовании низкоскоростной зоны на глубинах от 10 до 20 км. Главный надвиг (BNS) имеет вид листрического надвига в средней коре со смещением около 3.5 км и протяженностью 10 км, что превышает размер ячейки поля скорости. Он делит нижнюю и среднюю кору на две части. Другой надвиг того же направления идентифицируется к северу от BNS.Средняя кора Киангтанг блока имеет повышенный градиент скорости и пониженную мощность по.сравнению с блоком Лхаса. Южнее BNS средняя кора включает пододвинутый блок, чья южная граница может быть трассирована по изменению наклона скоростных изолиний. Несколько субгоризонтальных инверсионных разрывов относительно короткой протяженности и идентичного наклона могут быть прослежены в обоих блоках.
Различие может свидетельствовать о различном вещественном составе средней коры блоков Лхаса и Киангтанг. По геологическим данным блоки Лхаса и Киангтанг являются террейнами. Это может быть надвиг блока Куангтанг на блок Лхаса.
Средняя кора прослеживается до глубин от 40 км на юге до 28 км на севере. Скорость вблизи подошвы средней коры составляет около 6.4 км/с. Нижняя кора прослежена до глубины 48 км. Скорости в ней увеличиваются с глубиной от 6.4 до 6.8 км/с. Нижняя кора имеет постоянный скоростной градиент и общий наклон скоростных контуров, ее кровля совпадает с подошвой листрического надвига на севере.
Новый глубинный разрез по профилю INDEPTH III позволяет проследить известный структурный шов BNS на всю глубину коры, установить характер сочленения блоков Лхаса и Киангтанг, а также оценить различия в их строении. В целом разрез свидетельствует о различном характере деформаций в верхней и средней коре, что в свою очередь указывает на различную историю их формирования. Прежняя модель, полученная методом моделирования (Zhao et al., 2001), значительно менее подробна, не сjдержит указанных сведений (рис. 5.7).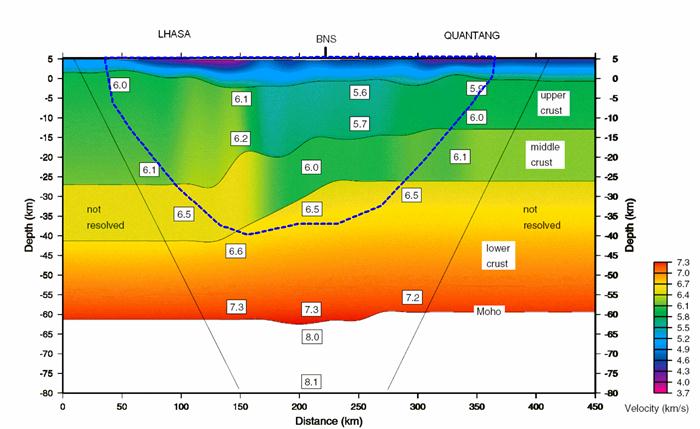
Вычисленный нами разрез хорошо соответствует модели структуры литосферы в Тибетско-Гималайском регионе (рис. 5.8), опубликованной в (Allegre et al., 1984). Эта модель является результатом 3-х годичной французско-китайской экспедиции в Тибет. Авторы статьи пришли к выводу, что сутура BNS, представляет собой листрический надвиг в южном направлении океанической коры на континентальную, возникший в процессе коллизии блока Лхаса и блока Киангтанг. Надвиги в этом же направлении по мнению Allegre et al. (1984) существуют южнее BNS.

Рис.5.8
Полученный нами новый глубинный разрез отвечает указанным представлениям, подтверждает и детализирует их, дает конкретные цифровые значения мощностей слоев, характера расслоенности разреза и формы тектонических нарушений, хотя мы не использовали при его построении никаких априорных данных, кроме наблюденных времен первых вступлений.
Модель Zhao et al (рис.5.7) и новый разрез (рис. 5.6) подобны в отношении средней скорости. Новый разрез отличается от модели Zhao et al волноводом в средней коре, так же как и изменчивостью скорости в вертикальном и горизонтальных направлениях внутри слоев. Кровля верхней коры практически та же самая в обоих разрезах. Это инверсионная граница и она видна в поле скоростных контуров как линия резкого понижения скорости и как граница показанная непрерывной линией на разрезе модели Zhao et al. Высокоскоростные слои в верхней коре блока Lhasa на новом глубинном разрезе по своему положению больше чем наполовину перекрывают вертикальный блок повышенных скоростей в модели Zhao et al.
Новый глубинный разрез является, в целом, более гладким и естественным в геологическом смысле, чем модель Zhao et al. Достаточно внимательно рассмотреть сложную и резкую скоростную структуру в центральной части модели Zhao et al., которая показана тоном, а не изолиниями. Эту структуру образуют три резкие вертикальные скоростные границы раздела, расположенные на пикетах 100, 155 и 280 км, и простирающиеся на всю глубину верхней и средней коры.
Достоверность новой интерпретации. Следующее возражение может быть рассмотрено против разреза, который мы произвели.
Это то, что система наблюдений (5 взрывов) и данные только первых вступлений недостаточны для инверсии. Новый разрез, произведенный методом однородных функций, был проверен лучевым трассированием. Лучи и времена пробега вычислены с использованием программы SISM (Ефимова, 1973). Программа выполняет решение системы дифференциальных уравнений, вычисляет лучи и времена пробега волн вдоль них. Скорость в разрезе задана значениями в узлах прямоугольной сетки. Существует два вида задач лучевого трассирования, которые называются начальная задача и граничная задача лучевого трассирования. Программа SISM основана на решении начальной задачи, когда в качестве начальных данных задаются точка, через которую проходит луч, и направление луча в этой точке. Эта задача решается наиболее точно и устойчиво. Однако в этом случае невозможно указать точку на поверхности, куда должен придти, вышедший из источника луч. Поэтому рассчитанные нами лучевые диаграммы для всех реальных взрывов позволяют оценить рассчитанное время только в отдельных точках профиля, которые мы заранее не можем выбрать.

рис. 5.9
Лучи, вычисленные для наблюденных источников для нового разреза, показаны на Рис. 5.9. Рассматривая лучевые диаграммы, мы видим многочисленные лучи, имеющие точки поворота в средней коре. В области волновода лучи не имеют точек поворота. Лучи обходят и рассеиваются в областях разреза с повышенными скоростью и градиентом скорости и глубоко проникают туда, где скорость и ее градиент понижены. Это нормальное поведение лучей для двухмерно-неоднородных сред.
Сопоставление наблюденных и рассчитанных времен дается на рис.5.3 Крестиками показаны наблюденные времена (пики). Они соединены прямыми линиями. Кружками показаны времена, рассчитанные для нового глубинного разреза. Среднеквадратическое отклонение вычисленных времен от наблюденных составляет 0.17 s. Вычислено всего 540 значений времен для
.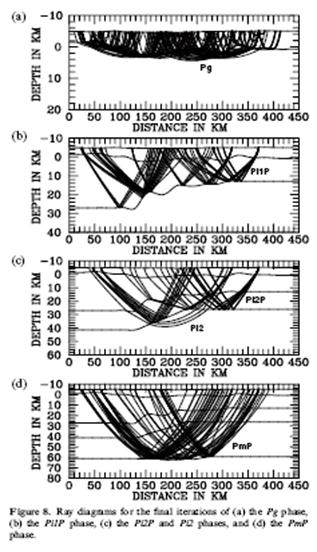
Рис.5.10
нового глубинного разреза Тонкие непрерывные линии - это теоретические годографы для Zhao et al. модели. Хотя теоретические годографы, приведенные в Zhao et al. (2001) являются непрерывными линиями, им отвечает огромный разрыв в глубинной модели. Ни один луч не имеет точек поворота на глубинах от 10 до 35 км для этой модели. Иными словами, лучи, которые сформировали теоретические годографы до времен 11 с, не проникают глубже 10 км. Кроме того, как видно из рис. 5.3, времена, рассчитанные для нового глубинного разреза, лучше согласуются с наблюденными годографами в отношении значений кажущейся скорости, чем теоретические годографы для Zhao модели.
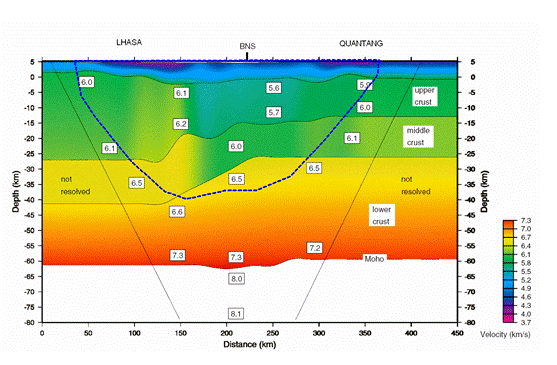
Рис.5.10
Дискуссия и обсуждение. Идентификация волн на множестве двухмерных однородных функций есть автоматический процесс, который имеет единственное решение.
Мы вычислили автоматически методом однородных функций сейсмический разрез, который включает волновод. Мы не использовали какой-либо начальной модели или другой априорной информации. Три обстоятельства подтверждают достоверность нового разреза.
Структуры, полученные на окончательном разрезе, имеют отображение в наблюденном временном поле.
Теоретические времена близки к наблюденным и лучи им соответствующие проникают на полную глубину разреза
Разрез, который мы получили, хорошо согласуется с геологической и геофизической моделью литосферной структуры для Тибет-Гималайского региона.
Окончательный глубинный разрез содержит новую информацию и также дает конкретные численные значения для скоростей продольных волн, мощностей слоев, характера расслоенности и формы надвигов.
Преимущества сейсмического разреза вдоль профиля INDEPH III может быть объяснено, фактом, что реальное скоростное распределение было аппроксимировано бесконечномерной функцией двух координат при инверсии годографов. Также очень важно, что свойства аппроксимирующей функции адекватны свойствам реальных геологических сред. Метод однородных функций это метод простой инверсии. Процедура инверсии при использовании этого метода не занимает много времени, потому что это полностью автоматическая процедура
СПИСОК ЛИТЕРАТУРы
Ефимова E.A. Решение.прямой задачи сейсморазведки численными методами // Вестник Моск. ун-та, Сер. 4. Геология. 1973. С. 118-122.
Пийп В.Б. Новые методы интерпретации сейсмических волновых полей в средах с переменными скоростями // Вестник Моск. ун-та. Сер. 4. Геология. 1984. № 3. С. 86-95..
Пийп В.Б. Локальная реконструкция сейсмического разреза по данным преломленных волн с использованием однородных функции // Физика Земли.1991. № 10. С. 844-850.
Пузырев Н.Н. К теории интерпретации точечных сейсмических зондирований // Геология и Геофизика. 1963. № 9, С. 85-99.
Allegre C.J., et al. Structure and evolution of the Himalaya-Tibet orogenic belt // Nature. 1984.N 307. P. 17-22.
Piip V.B., 2001. 2D inversion of refraction traveltime curves using homogeneous functions // Geophysical prospecting. 2001. V. 49. P. 461-4826.
Zhao W., Mechie J., Brown L.D., et al. Crustal structure of central Tibet as derived from project INDEPTH wide angle seismic data // Geophys. J. Int. 2001. V. 145, P. 486-498
Zelt C. A. and Smith R. B. Seismic traveltime inversion for 2-D crustal velocity structure // Geophysical Journal International. 1992. V.108. P. 16-34.
Приложение. Устойчивость решения обратной кинематической задачи сейсмики на множестве двухмерных однородных скоростных функций
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1527; Нарушение авторских прав?; Мы поможем в написании вашей работы!