
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Наибольшее и наименьшее значение функции
|
|
|
|
Пусть функция y=f(x) непрерывна на отрезке [ a;b ]. Как известно, такая функция достигает своих наибольшего и наименьшего значений. Эти значения функция может принять либо во внутренней точке 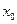 отрезка [ a;b ], либо на его концах.
отрезка [ a;b ], либо на его концах.
Получаем следующее правило нахождения наибольшего и наименьшего значений функции на [ a;b ]:
1. Найти критические точки функции на интервале (a;b).
2. Вычислить значения функции в найденных критических точках.
3. Вычислить значения функции на концах отрезка.
4. Среди всех вычисленных значений выбрать наибольшее и наименьшее.
Пример: Найти наибольшее и наименьшее значение функции 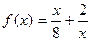 на отрезке
на отрезке
[1;6]. 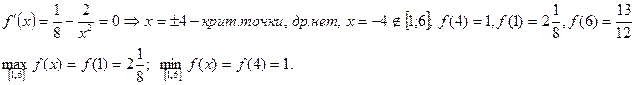
Замечание 1: Если функция y=f(x) на отрезке [ a;b ] имеет лишь одну критическую точку и она является точкой максимума (минимума), то в этой точке функция принимает наибольшее (наименьшее) значение.
Пример: На прямой y=2x найти такую точку, чтобы сумма квадратов расстояний от
нее до точек А(2;0) и в(0;4) была наименьшей.
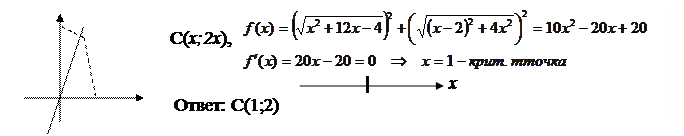
Замечание 2: Если функция не имеет критич. точек на отрезке, то на нем функция возрастает или убывает и свое наиб. (наим.) значение принимает на концах отрезка.
Пример: Чему равно наибольше значение функции f(x)=sin(sinx)?
1) 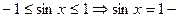 наибольшее значение;
наибольшее значение;
2) f(z)=sin z возрастает при 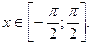 Этот отрезок включает отрезок [-1;1]. Значит,
Этот отрезок включает отрезок [-1;1]. Значит,
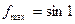 .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 634; Нарушение авторских прав?; Мы поможем в написании вашей работы!