Эмпирическая функция распределения

Определение. Эмпирической функцией распределения (функцией распределения выборки) называют функцию F* (х), определяющую для каждого значения х относительную частоту события Х < х.

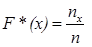, где n_x – число вариантов (число х_i) меньших х, n – объем выборки.

Свойства:

1. Значение F* (х) принадлежит отрезку [0, 1]: ;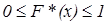

2. F* (х) – неубывающая функция;

3. Если x_i – наименьшее наблюдаемое значение, х_k – наибольшее наблюдаемое значение, то F* (х) = 0 при ;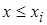

F* (х) = 1 при .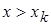

Пример 7. Пусть результаты наблюдений представлены в виде следующего ДСР (данные примера 3 из § 3):

xi
wi	1/20	2/20	3/20	4/20	5/20	3/20	2/20

Объем выборки по условию примера n = 20. Наименьшая варианта равна 1, значит, m_x = 0 при x ≤ 1. Тогда 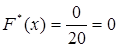при x ≤ 20. Следующая варианта в ранжированном ряду равна 2. Рассмотрим 1 < x ≤ 2. В этом случае неравенство X < x выполняется для варианты x ₁ = 1. Эта варианта встречается один раз в выборке, поэтому m_x = 1 и 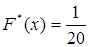. Далее, если 2 < x ≤ 3, то неравенство X < x выполняется для вариант x ₁ = 1 и x ₂ = 2. Варианта x ₁ встречается один раз, а варианта x ₂ встречается два раза, поэтому m_x = 1 + 2 = 3 и 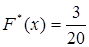и так далее. Следовательно, аналитически функция 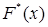определяется следующим образом:

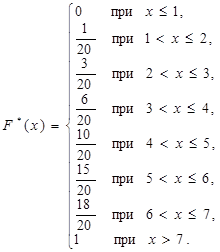
Замечание. Вообще, если известен ДСР, то 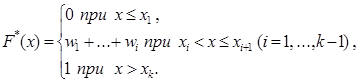  Здесь xk совпадает с xmax.

Суммы 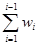обычно называются накопленными относительными частотами. 

Построим график 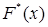по данным примера 7.

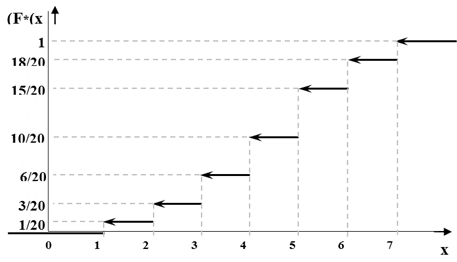
Рис. 5

Если результаты наблюдений представлены в виде ИСР, то выборочную функцию строят иначе.

Пример 8. Рассмотрим для этого следующий вариационный ряд:

[ xi; xi +1)	[0; 10)	[10; 20)	[20; 30)	[30; 40)	[40; 50)
wi	1/30	2/30	3/30	4/30	5/30
[ xi; xi +1)	[50; 60)	[60; 70)	[70; 80)	[80; 90)	[90; 100]
wi	5/30	4/30	3/30	2/30	1/30

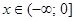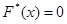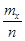Очевидно, что для функция , так как m_x = 0. Пусть теперь . В этом случае число не определено, так как неизвестно, сколько выборочных значений случайной величины, принадлежащих этому интервалу, меньше x. Если x = 10, то m_x = 1. Следовательно, в этом случае 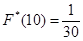. Рассуждая аналогично, убеждаемся, что точками, в которых значение функции 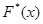можно определить, являются правые концы интервалов и все точки интервала 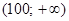. Значение функции 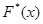в указанных точках можно записать в виде таблицы:

x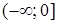

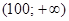
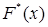
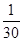
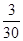
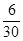
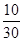
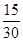
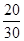
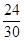
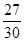
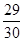
Так как эта таблица определяет функцию 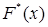не полностью (не для всех x известны ее значения), то при графическом изображении данной функции ее доопределяют, соединив точки графика, соответствующие концам интервалов отрезками прямой. В результате график функции 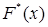будет представлять собой непрерывную линию. Подобный график выборочной функции 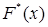часто называют кумулятивной кривой (от англ. accumulation – накопление). 

Построим график 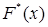по данным примера 8.

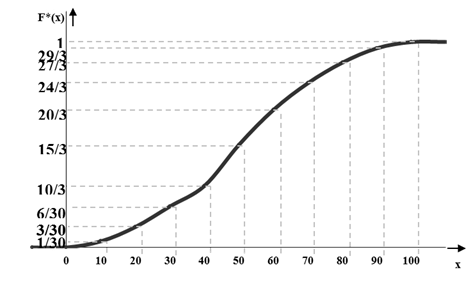
Рис. 6

Дата добавления: 2014-01-07