Динамика вращательного движения

ЛЕКЦИЯ 1.4

Момент силы. Момент импульса. Рассмотрим материальную точку М массой m, движущуюся в некоторой системе отсчета относительно точки О под действием силы F (см. рис. 1). Моментом силы F относительно точки О называется векторная величина

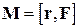. (1)

Моментом импульса точки М относительно точки О называется векторная величина

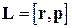. (2)

Модули момента импульса и момента силы соответственно равны

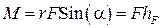, (3)

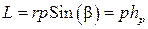. (4)

Величины 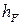и 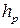называются плечом силы F и импульса p относительно точки О соответственно. Как мы видим, модули M и L зависят от точки О, относительно которой рассматривается движение материальной точки.

Основной закон динамики вращательного движения для материальной точки. Продифференцируем соотношение (2) по времени, получим

.

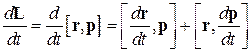Заметим теперь, что

,

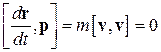а

.

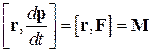Таким образом,

. (5)

Соотношение (5) в векторной форме выражает основной закон динамики вращательного движения. Выражение (5) мы получили пока применительно к материальной точке.

Вращательное движение твердого тела относительно неподвижной оси. Момент инерции материальной точки и твердого тела. Перейдем теперь к рассмотрению вращательного движения твердого тела, осуществляемого под действием приложенных к нему сил. Как мы же установили, в поступательном движении мерой интенсивности воздействия одного тела на другое является сила, а количественной мерой инертности тела по отношению к этому воздействию является физическая величина, называемая массой. Из повседневного опыта известно, что при вращательном движении, когда силовое воздействие осуществляется с целью придать некоторому телу вращение относительно какой-либо оси, интенсивность воздействия зависит не только от величины приложенной силы, но и от расстояния от точки приложения силы до оси (пример с закручиванием гаек). В связи с этим при рассмотрении вращения тел и вводится понятие момента силы. Ясно, что, как и в случае поступательного движения, попытка придать телу, обладающему массой, вращение будет характеризоваться некоторой инерционностью, выражающейся в том, что тело приобретет желаемую угловую скорость вращения не сразу, а через некоторое время. Из опыта известно, что степень инерционности в данном случае будет зависеть не только от массы тела, но и от его геометрии, от того, каким образом, на каких расстояниях от оси вращения находятся отдельные части (элементы) тела. Для характеристики меры инертности тела при вращательном движении вводится физическая величина, называемая моментом инерции тела. Сначала рассмотрим это понятие применительно к материальной точке.

Рассмотрим материальную точку М находящуюся на расстоянии r от оси ОО ' (см. рис. 2). Моментом инерции этой точки относительно рассматриваемой оси называется величина

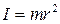. (6)

Заметим, теперь, что

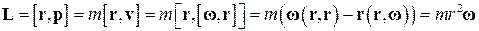
или

.

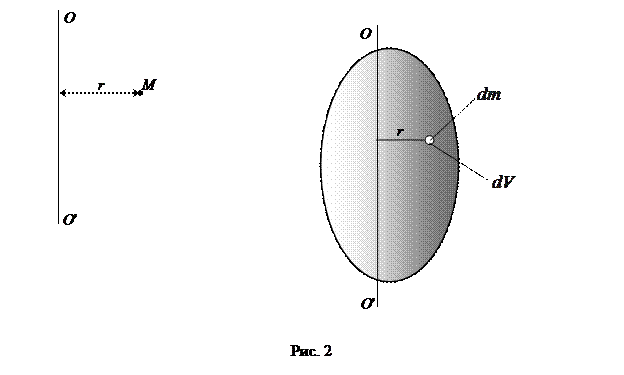
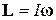Как мы видим, момент инерции, как и масса, есть величина не отрицательная. Теперь рассмотрим твердое тело, которое расположено относительно введенной нами оси так, как показано на рис. 2. Выделим в теле элемент объем и массой 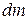, находящийся на расстоянии r от оси. Так как размеры этого элемента малы, то его можно считать материальной точкой. Тогда момент инерции этого элемента относительно оси можно записать, пользуясь формулой (6):

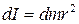. (7)

Момент инерции тела относительно рассматриваемой оси, очевидно, будет складываться из моментов инерции составляющих его элементарных частей, т.е.

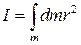. (8)

Формула (8) является основной при расчете моментов инерции твердых тел произвольной формы. Важно отметить, что при суммировании (интегрировании) элементарных моментов инерции величина r будет меняться, так как каждому элементу тела массой 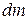будет соответствовать свое расстояние от оси r. В связи с этим в (8) величина r не может быть вынесена из под знака интеграла.

Заметим, что, используя представление 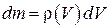, (8) можно переписать в виде

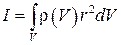. (9)

Если тело однородное, то плотность во всех точка его объема постоянна и одинакова, так что

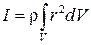. (10)

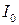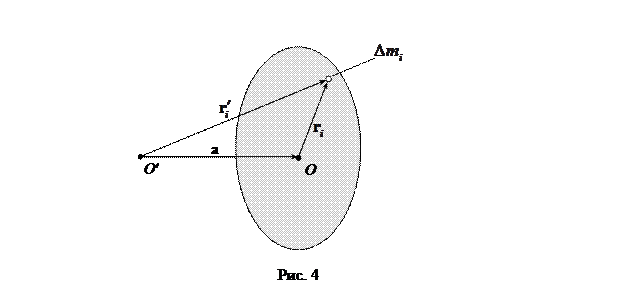
Предположим, что момент инерции относительно этой оси известен и равен . Вычислим момент инерции этого тела относительно оси O'Y', параллельной оси OY и отстоящей от нее на расстояние 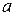. Разобьем объем тела на N элементов достаточно малого размера, чтобы их можно было считать материальными точками.. Расстояние от элемента массой 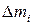до оси OY равно 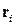. От оси O'Y' этот же элемент отстоит на расстояние 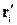. Из рис. 4 видно, что

.

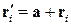Возводя это соотношение в квадрат, получим

.

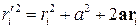Умножая обе части полученного равенства на 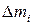, получим

.

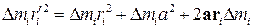Суммируя по всем элементам, получим

.

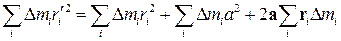Последнее соотношение можно переписать в виде

.

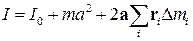Заметим также, что

,

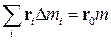где 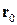- вектор, проведенный от оси OY к центру масс тела. Так как ось OY проходит через центр масс, вектор 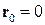. В итоге имеем

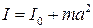. (13)

Соотношение (13) представляет собой математическую форму записи теоремы Штейнера: момент инерции I относительно произвольной оси равен сумме момента инерции I ₀ относительно оси, параллельной данной и проходящей через центр масс тела, и произведения массы тела m на квадрат расстояния а между осями.

Вывод основного закона динамики вращательного движения твердого тела. Пусть на каждый элемент тела массой 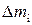действует сила 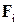. Для каждого i -го элемента справедлива формула (5):

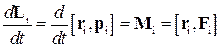. (14)

Перепишем (14) в виде

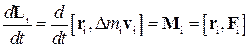. (15)

Ранее мы уже получали связь между угловой и линейной скоростями точки при ее вращении вокруг оси в виде

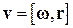. (16)

С учетом (16) можем записать

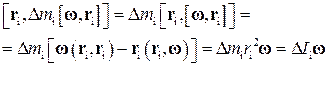, (17)

где 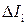- момент инерции элемента массой 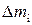относительно выбранной оси. В (17) мы учли, что угловая скорость всех элементов абсолютно твердого тела должна быть одинаковой.

Теперь (15) можно записать в виде

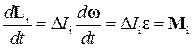. (18)

Проведем суммирование по всем N элементам нашего тела, получим

.

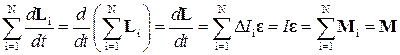Как мы видим, это соотношение может быть записано в одной из трех форм

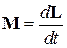, (19)

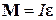, (20)

выражающих в математической форме основной закон динамики вращательного движения твердого тела: результирующий момент сил, приложенных к телу, равен изменению во времени момента импульса этого тела относительно рассматриваемой оси или результирующий момент сил, приложенных к телу, равен произведению момента инерции этого тела относительно рассматриваемой оси на его угловое ускорение.

Закон сохранения момента импульса. Как и в случае вывода закона сохранения импульса рассмотрим механическую систему, состоящую из N взаимодействующих частиц (материальных точек). Вновь обозначим силу, действующую на частицу с номером i со стороны частицы с номером j через 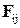Предположим снова, что кроме внутренних сил на каждую частицу действуют также внешние силы, равнодействующую которых для 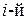частицы обозначим через 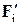Запишем уравнение движения для всех N материальных точек, получим

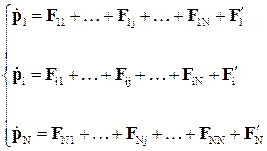(21)

Умножим каждое из уравнений системы (21) слева и справа векторно на 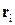, получим

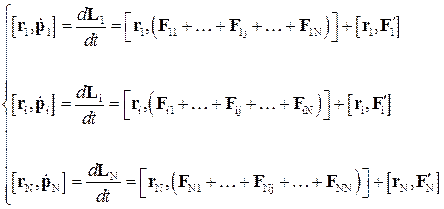(22)

Складывая уравнения системы, получим

,

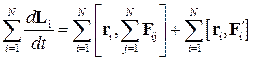или

,

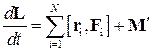где L, F _i и М ' – суммарный момент импульса системы точек, равнодействующая внутренних сил, действующих на i -ю точку и результирующий момент внешних сил, действующих на систему материальных точек соответственно.

Покажем, что

.

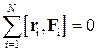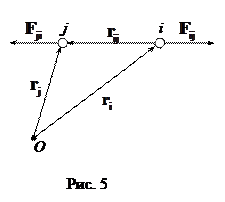Рассмотрим рис. 5, на котором представлена пара взаимодействующих тел с номерами i и j. По третьему закону Ньютона 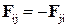. Видно, что

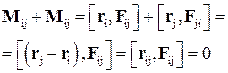
Таким образом,

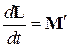. (23)

Соотношение (23) выражает собой закон изменения момента импульса системы материальных точек: изменение во времени момента импульса системы равно суммарному моменту действующих на нее внешних сил.

Из (23) в частности следует, что если на систему не действуют внешние силы или их сумма равна нулю (тогда и момент внешних сил равен нулю), то

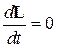. (24)

Соотношение (24) есть математическая форма записи закона сохранения момента импульса: изменение во времени момента импульса замкнутой механической системы равно нулю.

Гироскоп. Гироскопом называется массивное симметричное тело, вращающееся с большой скоростью вокруг оси симметрии. Если ось гироскопа неподвижна, то его момент импульса может быть записан в виде

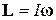, (25)

где 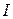- момент инерции гироскопа относительно оси симметрии, 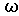- угловая скорость его вращения. Из (25) видно, что в этом случае вектор момента импульса параллелен оси гироскопа. Если ось гироскопа вращается с угловой скоростью 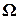вокруг какой-либо другой оси, проходящей через центр масс гироскопа, то (25) необходимо записать в виде

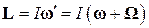. (26)

Как видно из (26), теперь вектор 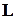уже не совпадает с осью гироскопа. Однако обычно 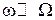, так что приближенно можно считать, что

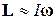. (27)

В дальнейшем будем считать, что .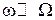

Рассмотрим гироскоп, представленный на рис. 6. Приложим к оси ОО гироскопа силы F и попробуем повернуть гироскоп вокруг оси 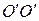. Мы увидим, что гироскоп поведет себя не так, как мы ожидали: ось гироскопа начнет поворачиваться не вокруг оси 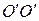, а вокруг 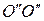. Такое необычное на первый взгляд поведение гироскопа получило название гироскопический эффект. Объяснить данный эффект можно на основе основного закона динамики вращательного движения. Действительно, пара сил 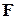, приложенная к оси гироскопа, создаст момент сил 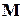, направленный так, как показано на рис. 6. Из основного закона динамики вращательного движения твердого тела следует, что за время 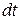вектор 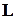момента импульса гироскопа получит приращение

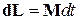, (28)

причем, как видно из (28), направление вектора 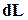сонаправлено с 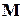. В результате по прошествии времени 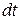вектор 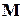, а следовательно и ось гироскопа, замет новое положение в пространстве, повернувшись на малый угол 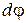вокруг оси .

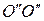Установим связь между вектором угловой скорости 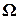вращения оси 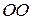относительно оси 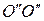вектором момента импульса гироскопа 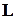и вектором момента приложенных сил 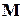. Из рис. 6 видно, что

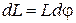. (29)

Из соотношения (28) получаем

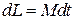. (30)

Разделив (29) на (30) и проведя несложные преобразования, получим

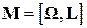. (31)

Соотношение (31) полученное при условии, что вектора 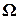и 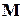перпендикулярны, справедливо и в общем случае произвольной взаимной ориентации указанных векторов.

При конструктивном исполнении гироскопа его ось закрепляется в подшипниках. Поэтому попытка повернуть принудительно ось гироскопа заданным образом приведет к возникновению сил, действующих со стороны оси гироскопа на подшипники. Эти силы называют гироскопическими. Если, например, принудительно повернуть ось гироскопа вокруг оси 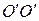так, как это показано стрелкой на рис. 6, то в подшипниках возникнут гироскопические силы, момент которых равен

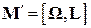. (32)

Применение гироскопа. Гирокомпас. (Самостоятельно).

Кинетическая энергия вращающегося тела. Рассмотрим еще раз рис. 2. Элемент тела массой 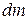, вращаясь вокруг неподвижно оси 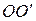на расстоянии 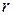от нее с угловой скоростью 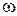, будем иметь линейную скорость движения 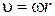. Кинетическая энергия этого элемента будет равна

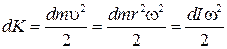. (33)

Интегрирование (33) даст, очевидно, кинетическую энергию вращательного движения твердого тела:

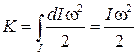, (34)

где 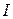- момент инерции тела относительно оси вращения.

Выражение для кинетической энергии тела при сложном движении. Пусть тело, представленное на рис. 2, совершает плоское движение так, как это показано на рис. 7. Как видно из рис. 7, движение произвольной точки М тела за малый интервал времени 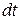можно представить как комбинацию двух видов движения: поступательного, определяемого вектором и вращательного, задаваемого вектором 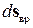, так что общее перемещение за время 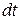будет .

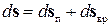Разделив обе части полученного соотношения на 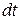, найдем, что

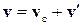, (35)

где 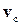, 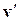- скорость поступательного движения центра масс тела 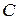и скорость вращения рассматриваемой точки относительно оси, проходящей через центр масс. Как мы уже выяснили, величину 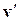можно представить в виде

.

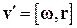Тогда для кинетической энергии элемента 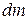, связанного с точкой 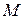тела получим

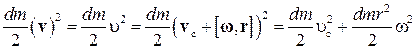. (36)

Интегрируя (36) получим

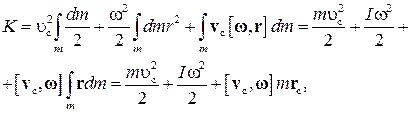
где 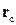- радиус-вектор центра масс тела.

Так как подвижную систему отсчета мы связали с центром масс тела, то, очевидно, что 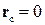. Тогда для кинетической энергии тела при сложном движении получаем

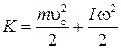, (37)

где 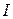- момент инерции тела относительно оси, проходящей через его центр масс.

Таким образом, кинетическая энергия тела при его произвольном плоском движении равна сумме кинетической энергии поступательного движения тела, происходящего со скоростью его центра масс, и вращательного движения тела вокруг его центра масс, происходящего с угловой скоростью .

Дата добавления: 2014-01-07