
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Механические колебания
|
|
|
|
ЛЕКЦИЯ 1.6
Колебаниями называются процессы, отличающиеся той или иной степенью повторяемости. В зависимости от физической природы колебания делят на механические, электромагнитные, электромеханические и т.д. Примером механической системы, совершающей колебания, могут служить в частности колебания грузика на пружине или шарика на нити. В зависимости от характера воздействия на механическую систему, совершающую колебания, различают свободные затухающие и незатухающие колебания, а также вынужденные колебания. Если механическую систему, находящуюся в состоянии устойчивого равновесия, вывести из этого положения путем какого-нибудь кратковременного воздействия, например, слегка качнуть шарик, подвешенный на нити, рукой, а затем предоставить ее самой себе, то возникают механические колебания. В примере с шариком на нити, эти колебания сопровождаются периодическим изменением угла отклонения нити от вертикального положения. Такие колебания, протекающие без внешнего периодического воздействия, называются свободными или собственными. Если начавшиеся колебания механической системы протекают без потерь энергии, то амплитуда колебаний остается постоянной в течение бесконечно долгого промежутка времени. Такие свободные колебания называются незатухающими. Как мы увидим, в случае малых по величине изменений во времени колеблющейся величины (угла отклонения нити в случае колебаний шарика на нити, или координаты грузика на пружине) эти изменения можно описать законом косинуса или синуса, т.е. гармонической функцией. Поэтому про свободные незатухающие колебания говорят также, что они гармонические. Если на механическую систему, совершающую колебания, действуют диссипативные силы, например, силы трения, то в результате рассеяния механической энергии системы амплитуда колебаний будет постепенно уменьшаться до тех пор, пока колебания не прекратятся совсем. Такие свободные колебания называются затухающими. Если же колебания происходят под действием внешней периодической силы, стимулирующей (иначе вынуждающей) эти колебания, то такие колебания называются вынужденными.
 Свободные незатухающие (гармонические) колебания.
Свободные незатухающие (гармонические) колебания.
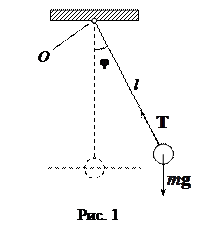
Математический маятник. Рассмотрим механическую систему в виде шарика радиусом  и массой
и массой  , подвешенного на нити длиной
, подвешенного на нити длиной  (см. рис. 1). Выведенный из положения равновесия, шарик начнет совершать колебания. Предположим, что сила трения, действующая на шарик со стороны молекул окружающей среды пренебрежимо мало. Будем считать также, что отсутствует и трение нити в точке подвеса О, и что нить достаточно жесткая для того, чтобы можно было пренебречь потерями энергии при ее деформациях растяжения и сжатия. При таких условиях рассматриваемые колебания будут незатухающими. Получим уравнение, описывающее изменение во времени угла
(см. рис. 1). Выведенный из положения равновесия, шарик начнет совершать колебания. Предположим, что сила трения, действующая на шарик со стороны молекул окружающей среды пренебрежимо мало. Будем считать также, что отсутствует и трение нити в точке подвеса О, и что нить достаточно жесткая для того, чтобы можно было пренебречь потерями энергии при ее деформациях растяжения и сжатия. При таких условиях рассматриваемые колебания будут незатухающими. Получим уравнение, описывающее изменение во времени угла  отклонения нити от положения равновесия. Из рис. 1 видно, что относительно оси
отклонения нити от положения равновесия. Из рис. 1 видно, что относительно оси  , проходящей через точку О перпендикулярно чертежу, шарик будет совершать вращательные движения. Запишем для шарика основной закон динамики вращательного движения относительно оси
, проходящей через точку О перпендикулярно чертежу, шарик будет совершать вращательные движения. Запишем для шарика основной закон динамики вращательного движения относительно оси  . Будем иметь
. Будем иметь
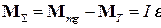 , (1)
, (1)
где  - суммарный момент сил, действующих на шарик, взятый относительно оси
- суммарный момент сил, действующих на шарик, взятый относительно оси 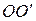 ,
, 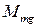 ,
, 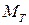 - моменты силы тяжести и силы натяжения нити,
- моменты силы тяжести и силы натяжения нити,  ,
, 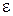 - момент инерции системы «шарик - нить» относительно оси
- момент инерции системы «шарик - нить» относительно оси 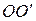 и угловое ускорение системы соответственно.
и угловое ускорение системы соответственно.
Из рис. 1 видно, что  , а
, а 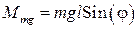 . Предположим, что масса шарика
. Предположим, что масса шарика 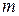 значительно больше массы нити, а радиус шарика
значительно больше массы нити, а радиус шарика  много меньше длины нити
много меньше длины нити  , тогда момент инерции системы относительно оси
, тогда момент инерции системы относительно оси 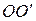 будет равен монету инерции шарика относительно этой оси, причем шарик можно считать материальной точкой, т.е.
будет равен монету инерции шарика относительно этой оси, причем шарик можно считать материальной точкой, т.е. 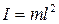 . Из рис. 1 видно также, что вектор φ поворота нити и вектор
. Из рис. 1 видно также, что вектор φ поворота нити и вектор  противоположны по направлению. Сделав эти замечания, теперь можем записать, что
противоположны по направлению. Сделав эти замечания, теперь можем записать, что
 . (2)
. (2)
Рассматривая малые колебания шарика, при условии 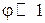 , т.е.
, т.е. 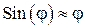 , придем к уравнению
, придем к уравнению
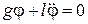 . (3)
. (3)
Приведя (3) к каноническому виду, получим
 , (4)
, (4)
где 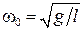 .
.
Уравнение (4) представляет собой линейное однородное дифференциальное уравнение (ЛОДУ) второго порядка относительно переменной φ. Известно, что записанное таким образом уравнение, представляет собой уравнение гармонических колебаний, решение которого имеет вид
 , (5)
, (5)
где 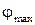 ,
,  и
и 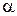 есть амплитуда, циклическая частота и начальная фаза колебаний соответственно. Период колебаний определяется по формуле
есть амплитуда, циклическая частота и начальная фаза колебаний соответственно. Период колебаний определяется по формуле
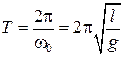 .
.
Зная характер изменения с течением времени угла отклонения нити, можно записать выражения, характеризующие изменение во времени угловой скорости и ускорения движения шарика. Согласно определению
 , (6)
, (6)
 , (7)
, (7)
где  и
и 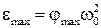 - амплитудные значения угловой скорости и ускорения соответственно.
- амплитудные значения угловой скорости и ускорения соответственно.
Заметим теперь, что
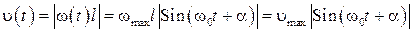 , (7)
, (7)
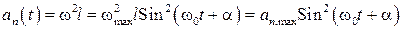 , (8)
, (8)
где 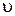 и
и 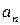 есть модули линейной скорости и нормального ускорения шарика.
есть модули линейной скорости и нормального ускорения шарика.
Из (5) и (7) следует, что
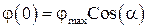 , (9)
, (9)
 . (10)
. (10)
Взяв отношение (10) к (9), получим формулы, позволяющие определить начальную фазу и амплитуду колебаний
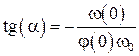 , (11)
, (11)
 . (12)
. (12)
Найдем теперь выражения для кинетической, потенциальной и полной механической энергий шарика.
Согласно определению
 .
.
Из (7) получаем
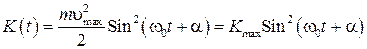 , (13)
, (13)
где 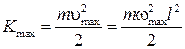 .
.
 Изменение потенциальной энергии шарика связано с работой силы тяжести. Найдем это изменение для элементарного перемещения
Изменение потенциальной энергии шарика связано с работой силы тяжести. Найдем это изменение для элементарного перемещения  шарика по траектории. Из рис. 2 следует, что
шарика по траектории. Из рис. 2 следует, что
 . (14)
. (14)
Взяв интеграл от этого выражения, найдем
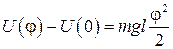 . (15)
. (15)
Взяв за нулевой уровень потенциальной энергии уровень, соответствующий положению равновесия шарика, получим
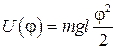 . (16)
. (16)
Принимая во внимание (5), перепишем (16) в виде
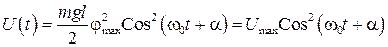 . (17)
. (17)
Полная механическая энергия рассматриваемой замкнутой механической системы рана
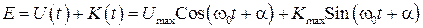 . (18)
. (18)
Заметим, что
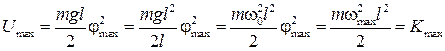 .
.
Тогда
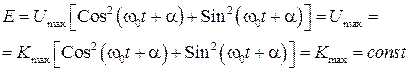 (19)
(19)
Графики зависимостей  показаны на рис. 3. Из рис. 3 видно, что период колебаний значений потенциальной и кинетической энергий шарика вдвое меньше периода колебаний значения угла, угловой скорости и ускорения. Соответственно, частота колебаний потенциальной и кинетической энергий шарика будет равна
показаны на рис. 3. Из рис. 3 видно, что период колебаний значений потенциальной и кинетической энергий шарика вдвое меньше периода колебаний значения угла, угловой скорости и ускорения. Соответственно, частота колебаний потенциальной и кинетической энергий шарика будет равна
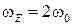 . (20)
. (20)
Заметим, что шарик, совершающий гармонические колебания, подчиняющиеся полученным уравнениям, называется математическим маятником. Согласно указанным выше допущениям колебания шарика на нити можно считать колебаниями математического маятника только тогда, когда:
1) шарик совершает гармонические колебания, которые будут иметь место только в случае отсутствия потерь энергии и малой амплитуды колебаний;
2) размеры шарика значительно меньше размеров длины подвеса, иначе говоря, когда шарик можно считать материальной точкой.
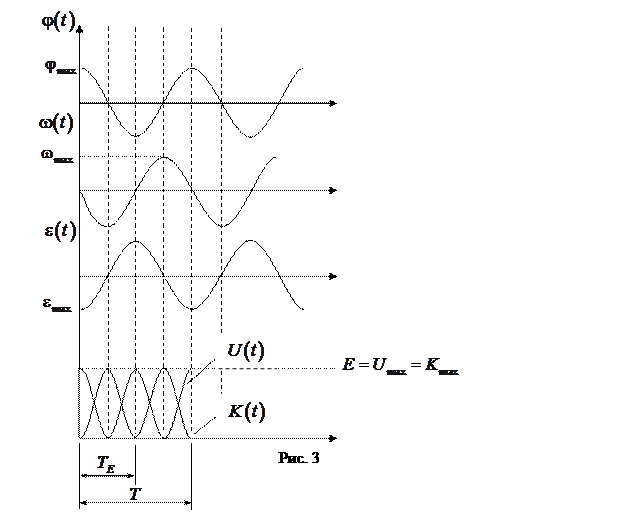
По аналогии с только что рассмотренными колебаниями шарика можно получить соответствующие выражения для гармонических колебаний грузика на пружине.
Пружинный маятник. Рассмотрим теперь малые колебания груза массой m, закрепленного на пружине жесткостью k (см. рис. 4). Как видно из рис. 4, в отсутствие сил трения на груз вдоль оси ОХ будет действовать только сила упругости:
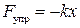 , (21)
, (21)
где k – коэффициент жесткости пружины, которая согласно второму закону Ньютона должна быть равна произведению массы груза на его ускорение, т.е.
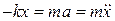 . (22)
. (22)
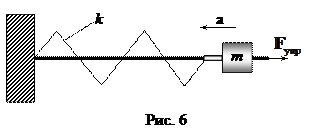 Как и ранее приведем (22) к каноническому виду:
Как и ранее приведем (22) к каноническому виду:
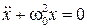 . (23)
. (23)
Как мы видим, вновь получается ЛОДУ, решение которого полностью идентично ранее рассмотренному. Теперь, однако, выражение для частоты собственных колебаний маятника имеет вид
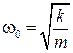 . (23)
. (23)
Соответствующие выражения для координаты, скорости, ускорения, кинетической и потенциальной энергий будут иметь вид
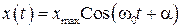 , (24)
, (24)
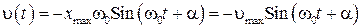 , (25)
, (25)
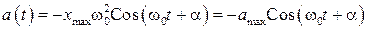 , (26)
, (26)
 , (27)
, (27)
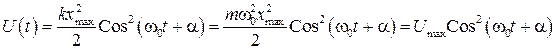 . (28)
. (28)
Как и в случае математического маятника, записав выражение для полной энергии, придем к соотношению
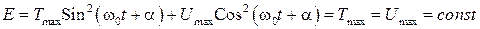 . (29)
. (29)
Физический маятник. Физическим маятником называется твердое тело, совершающее колебания вокруг некоторой оси, проходящей через тело (см. рис. 7). Обозначим расстояние от оси вращения до центра масс тела через  , а момент инерции тела относительно этой оси через
, а момент инерции тела относительно этой оси через  . Массу тела будем считать равной
. Массу тела будем считать равной 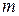 . Согласно основному закону динамики вращательного движения можем записать, что
. Согласно основному закону динамики вращательного движения можем записать, что
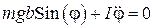 . (30)
. (30)
Так как 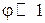 , то
, то 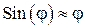 , так что
, так что
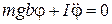 . (31)
. (31)
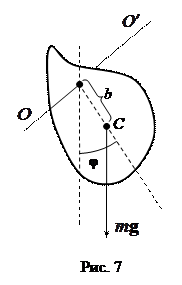 Вновь приведем (31) к каноническому виду:
Вновь приведем (31) к каноническому виду:
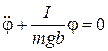 , (32)
, (32)
или
 , (33)
, (33)
где 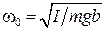 .
.
Поскольку уравнение (33) идентично (4), то с учетом выражения для 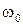 справедливы соотношения (5) – (20).
справедливы соотношения (5) – (20).
Свободные затухающие колебания. Рассматривавшееся нами ранее условие об отсутствии в системе диссипативных сил, очевидно, является абстракцией. В реальных колебательных системах в той или иной форме присутствуют диссипативные силы. В частности всегда существует сила трения. Наличие диссипативных сил, как уже отмечалось приводит к рассеянию механической энергии колебательной системой. Амплитуда колебаний при этом постепенно уменьшается. Ясно, что скорость убывания амплитуды колебаний будет зависеть от интенсивности процесса диссипации энергии, в частности, например, от величины силы трения. Если при выводе системы из положения равновесия возникающие силы трения слишком велики, то колебания либо быстро затухают, либо могут и вовсе не возникнуть.
Получим уравнение свободных затухающих колебаний на примере колебаний математического маятника, происходящих в воздухе. Теперь, в отличие от ранее рассматривавшегося случая, учтем, что на шарик со стороны молекул воздуха будет действовать сила вязкого трения. Если амплитуда и скорость колебаний маятника малы, то сила вязкого трения будет примерно пропорциональна линейной скорости движения шарика, т.е.
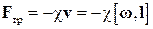 , (34)
, (34)
где  - коэффициент вязкого трения.
- коэффициент вязкого трения.
Момент сил трения тогда запишется в виде
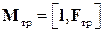 . (35)
. (35)
Теперь основной закон динамики вращательного движения для маятника в проекции на ось вращения запишется в следующем виде
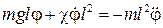 ,
,
или
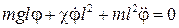 . (36)
. (36)
Приведем (36) к каноническому виду, получим
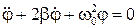 , (37)
, (37)
где 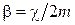 - коэффициент затухания,
- коэффициент затухания, 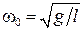 - собственная частота колебаний системы.
- собственная частота колебаний системы.
Будем искать решение (37) в виде
 ,
,
где 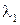 и
и  - корни характеристического уравнения
- корни характеристического уравнения
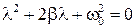 . (38)
. (38)
Решая, находим, что
 .
.
Рассмотрим случай, когда коэффициент затухания 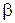 мал, тогда
мал, тогда 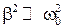 . Введем обозначение
. Введем обозначение
 . (39)
. (39)
Тогда
 .
.
Корнями уравнения (38) в этом случае будут
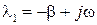
и
 .
.
Теперь можем записать, что

Возьмем действительную часть от последнего соотношения, получим
 .
.
В общем случае с учетом начальной фазы колебаний получим
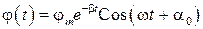 . (40)
. (40)
Итак, мы получили дифференциальное уравнение свободных затухающих колебаний (37) и его решение в виде (40). Из (40) видно, что 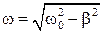 есть не что иное, как частота затухающих колебаний. Эта частота, вообще говоря, не равна
есть не что иное, как частота затухающих колебаний. Эта частота, вообще говоря, не равна 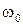 . Заметим, что функция, определяемая соотношением (40), может быть записана в виде
. Заметим, что функция, определяемая соотношением (40), может быть записана в виде
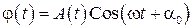 , (41)
, (41)
где 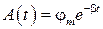 - амплитуда затухающих колебаний, которая как мы видим, зависит от времени.
- амплитуда затухающих колебаний, которая как мы видим, зависит от времени.
График колебательного процесса представлен на рис. 8.
 Как видно из графика, затухающие колебания не являются гармоническими ввиду того, что амплитуда колебаний есть монотонно убывающая функция времени. Тем не менее, по графику видно, что функция
Как видно из графика, затухающие колебания не являются гармоническими ввиду того, что амплитуда колебаний есть монотонно убывающая функция времени. Тем не менее, по графику видно, что функция  повторяет себя по виду на каждом интервале времени
повторяет себя по виду на каждом интервале времени
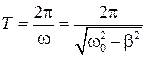 ,
,
что можно интерпретировать как наличие у функции периода колебаний длительностью  .
.
Логарифмический декремент. Добротность. Затухание колебаний принято характеризовать величиной, называемой логарифмическим декрементом затухания
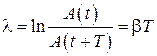 . (42)
. (42)
Физический смысл этой величины состоит в следующем. Пусть за  полных колебаний их амплитуда уменьшилась в
полных колебаний их амплитуда уменьшилась в 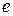 раз. Тогда
раз. Тогда
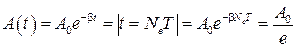 ,
,
и, следовательно,
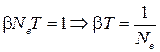 .
.
Теперь видно, что
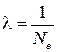 , (43)
, (43)
т.е. логарифмический декремент есть величина, обратная количеству колебаний, за которое амплитуда колебаний уменьшается в 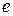 раз.
раз.
Добротностью колебательной системы называется величина
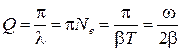 . (44)
. (44)
Если затухание мало, то 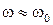 , так что
, так что
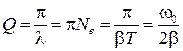 . (45)
. (45)
Тогда, например, для колебаний математического маятника получим
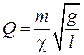 . (46)
. (46)
Энергия затухающих колебаний. Получим выражение для кинетической энергии затухающих колебаний. Рассматривая вращательное движение шарика вокруг оси 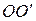 можем записать, что
можем записать, что
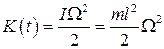 ,
,
где 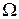 - угловая скорость вращения шарика.
- угловая скорость вращения шарика.
По определению
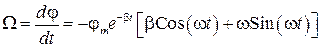 . (47)
. (47)
Введем обозначения
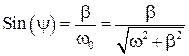 ,
, 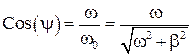 .
.
Тогда
 .
.
Теперь можно записать
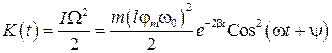 . (48)
. (48)
Очевидно, что
 . (49)
. (49)
Полная механическая энергия колебаний будет равна
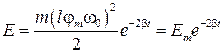 . (50)
. (50)
Как видно из (50), полная энергия диссипативной системы, как и следовало ожидать, убывает со временем. Убывание носит экспоненциальный характер.
Посмотрим теперь, как связана добротность колебательной системы с убылью ее энергии за один период колебаний. Последнюю величину можно представить в виде
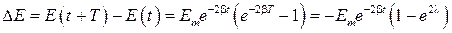 .
.
Найдем отношение
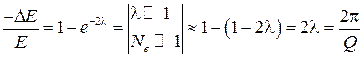 .
.
Таким образом,
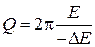 , (51)
, (51)
т.е. добротность колебательной системы с точностью до 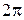 равна относительной убыли энергии колебательной системы за один период.
равна относительной убыли энергии колебательной системы за один период.
Вынужденные колебания. Пусть на нашу колебательную систему оказывается какое-либо периодическое воздействие. Предположим, что это воздействие можно представить в виде
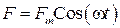 . (52)
. (52)
В таком случае уравнение основного закона динамики вращательного движения необходимо записать в виде
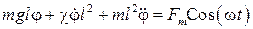 . (53)
. (53)
Снова приведем уравнение к каноническому виду:
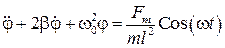 . (54)
. (54)
Представим (54) в комплексон виде:
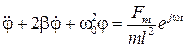 . (55)
. (55)
Решение ЛНДУ (55) будем искать в виде
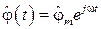 , (56)
, (56)
где 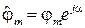 . Подставив (56) в (55), получим
. Подставив (56) в (55), получим
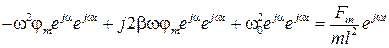 . (57)
. (57)
Приведем (57) к виду
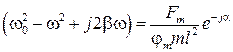 ,
,
и далее
 , (58)
, (58)
где
 .
.
Из (58) видно, что для выполнения равенства необходимо 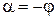 , т.е.
, т.е.
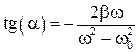 . (59)
. (59)
Таким образом, решение ЛНДУ (54) имеет вид
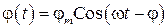 , (60)
, (60)
где
 ,
,
а 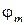 выражается соотношением
выражается соотношением
 . (61)
. (61)
 Явление резонанса. Как видно из (61), амплитуда колебаний
Явление резонанса. Как видно из (61), амплитуда колебаний 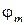 является функцией частоты вынуждающей силы. График этой функции имеет вид (см. рис. 9). Как видно из графика при приближении частоты вынуждающей силы к некоторому значению (как мы увидим, это значение равно собственной частоте колебаний системы) происходит резкое увеличение амплитуды колебаний, при этом говорят, что колебания входят в резонанс. Резонансом называется резкое возрастание амплитуды колебаний колебательной системы при приближении частоты колебаний вынуждающей силы к собственной частоте колебаний колебательной системы. Определим условие резонанса, исследуем на экстремум выражение (61). Будем иметь
является функцией частоты вынуждающей силы. График этой функции имеет вид (см. рис. 9). Как видно из графика при приближении частоты вынуждающей силы к некоторому значению (как мы увидим, это значение равно собственной частоте колебаний системы) происходит резкое увеличение амплитуды колебаний, при этом говорят, что колебания входят в резонанс. Резонансом называется резкое возрастание амплитуды колебаний колебательной системы при приближении частоты колебаний вынуждающей силы к собственной частоте колебаний колебательной системы. Определим условие резонанса, исследуем на экстремум выражение (61). Будем иметь
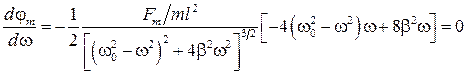 ,
,
откуда
 . (62)
. (62)
Амплитуда колебаний при этом достигает максимума
 . (63)
. (63)
Представление колебаний в векторном виде. Вектор-амплитуда.
Посмотрим еще раз на решение уравнения гармонических колебаний, имеющее в общем случае вид
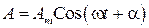 . (64)
. (64)
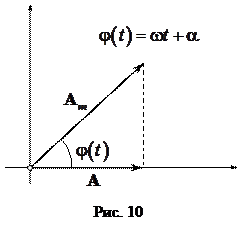 Этому уравнению можно поставить в соответствие векторную диаграмму (см. рис. 10). Таким образом, уравнение (64) можно представить в векторной форме:
Этому уравнению можно поставить в соответствие векторную диаграмму (см. рис. 10). Таким образом, уравнение (64) можно представить в векторной форме:
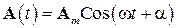 , (65)
, (65)
где  - вектор-амплитуда.
- вектор-амплитуда.
Векторные диаграммы удобно использовать для определения амплитуды результирующего колебания при сложении колебаний, имеющих одинаковое направление и одинаковую частоту. Приведем пример. Допустим, что имеются два колебания
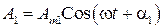 ,
,
 .
.
Представим эти колебания с помощью векторной диаграммы (см. рис. 11):
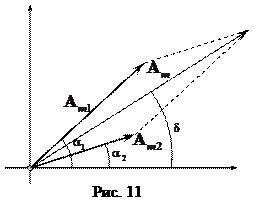 Как мы видим, амплитуда результирующего колебания равна
Как мы видим, амплитуда результирующего колебания равна
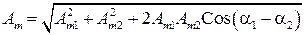 . (66)
. (66)
Начальная фаза результирующего колебания 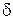 может быть найдена из соотношения
может быть найдена из соотношения
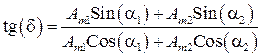 . (67)
. (67)
Сложение сонаправленных колебаний близких по частоте. Биения. Важным с практической точки зрения является случай сложения одинаково направленных гармонических колебаний в случае, когда частоты колебаний отличаются на малую величину  . В этом случае возникают так называемые биения, т.е. колебания с пульсирующей амплитудой. Посмотрим, каков в этом случае результат сложения колебаний. Итак, пусть имеются два гармонических колебания
. В этом случае возникают так называемые биения, т.е. колебания с пульсирующей амплитудой. Посмотрим, каков в этом случае результат сложения колебаний. Итак, пусть имеются два гармонических колебания
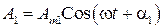 ,
,
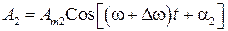 .
.
Для простоты предположим, что 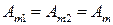 и
и 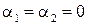 . Результирующее колебание будет иметь вид
. Результирующее колебание будет иметь вид
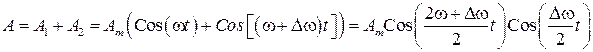 .
.
Таким образом,
 . (68)
. (68)
Здесь мы положили 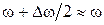 .
.
Как мы видим, выражение
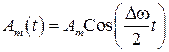 ,
,
представляющее собой амплитуду результирующего колебания, претерпевает периодические изменяется с частотой 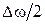 . Эти изменения происходят значительно медленнее, чем изменения величины
. Эти изменения происходят значительно медленнее, чем изменения величины 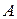 , задаваемые основной частотой
, задаваемые основной частотой 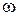 . График результирующего колебания представлен на рис. 12.
. График результирующего колебания представлен на рис. 12.
Сложение перпендикулярных колебаний. Фигуры Лиссажу. Рассмотрим два взаимно перпендикулярных колебания одинаковой частоты
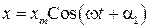 ,
,
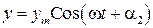 .
.
 Предположим, что
Предположим, что 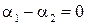 , тогда из векторной диаграммы (см. рис. 13) видно, что вектор результирующего колебания будет совершать колебания вдоль прямой, показанной пунктиром. Конец вектора при этом будет прописывать прямую линию.
, тогда из векторной диаграммы (см. рис. 13) видно, что вектор результирующего колебания будет совершать колебания вдоль прямой, показанной пунктиром. Конец вектора при этом будет прописывать прямую линию.
Нетрудно видеть, что к аналогичному результату приводит соотношение между начальными фазами колебаний
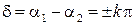 ,
,
где 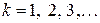 .
.
Если разность фаз колебаний
 ,
,
то
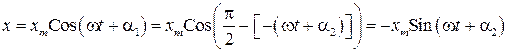 .
.
Но тогда
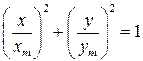 ,
,
т.е. имеем уравнение эллипса. Конец вектора амплитуды результирующего колебания будет описывать на плоскости эллипс. Ясно, что к аналогичному результату приведет любая разность фаз из ряда
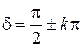 .
.
Заметим, что в частном случае при  получим окружность. При постепенном изменении
получим окружность. При постепенном изменении 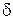 от
от 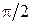 до
до 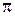 , или от
, или от 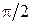 до 0 эллипс постепенно вырождается в прямую.
до 0 эллипс постепенно вырождается в прямую.
Из приведенных примеров видна область практического применения сложения перпендикулярных колебаний одинаковой частоты. Если подать два таких колебания на X и Y пластины осциллографа, что будет означать сложение перпендикулярных колебаний, то движение электронного луча по экрану будет соответствовать движению конца вектора амплитуды результирующего колебания. По наблюдаемой при этом траектории луча можно определит разность фаз складываемых колебаний.
Результаты сложения колебаний для различного соотношения между фазами колебаний представлены на рис. 14 и называются фигурами Лиссажу.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1535; Нарушение авторских прав?; Мы поможем в написании вашей работы!