
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Неинерциальные системы отсчета. Элементы СТО
|
|
|
|
ЛЕКЦИЯ 1.5
Понятие об неинерциальных системах отсчета. При формулировке законов Ньютона мы отметили, что эти законы выполняются только в инерциальных системах отсчета. Любая неинерциальная система отсчета движется относительно инерциальной с некоторым ускорением. Обозначим это ускорение символом  . Если ускорение тела в неинерциальной системе отсчета обозначить через
. Если ускорение тела в неинерциальной системе отсчета обозначить через 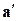 , то ускорение тела в инерциальной системе отсчета
, то ускорение тела в инерциальной системе отсчета  можно представить в виде
можно представить в виде
 . (1)
. (1)
Согласно второму закону Ньютона движение тела в инерциальной системе отсчета с ускорением  означает, что на тело действует сила
означает, что на тело действует сила
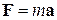 . (2)
. (2)
С учетом (2) соотношение (1) можно записать в виде
 , (3)
, (3)
или
 . (4)
. (4)
Из (3) видно, что в неинерциальной системе отсчета даже при условии, что  , тело будет иметь ускорение
, тело будет иметь ускорение  . Рассматривая соотношение (4), можно заметить, что ему можно придать вид, идентичный второму закону Ньютона:
. Рассматривая соотношение (4), можно заметить, что ему можно придать вид, идентичный второму закону Ньютона:
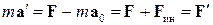 , (5)
, (5)
где
 (6)
(6)
есть так называемая сила инерции. Из (6) видно, что сила инерции противоположна по направлению ускорению  , с которым неинерциальная система отсчета движется относительно инерциальной системы отсчета.
, с которым неинерциальная система отсчета движется относительно инерциальной системы отсчета.
Пример с равномерным и равноускоренным движением вагона с подвешенным к его потолку шариком.
Важно понимать, что сила инерции является фиктивной. Фиктивность здесь надо понимать в том смысле, что возникающая сила не является ни результатом непосредственного воздействия одного тела на другое при механическом контакте, ни результатом воздействия одного тела на другое посредством какого-либо силового поля (например, гравитационного или электростатического). Действительно, движение вагона с ускорением как мы только что увидели приводит к изменению состояния движения шарика на нити: шарик отклоняется. Однако при этом непосредственно на шарик никаких дополнительных сил, кроме уже имевшихся силы гравитационного притяжения и силы натяжения нити, не действует. Таким образом, сила инерции не подпадает под данное нами ранее определение понятия силы, используемое в механике.
Центробежная сила инерции. Рассмотрим стержень, вращающийся с постоянной угловой скоростью  вкруг вертикальной оси
вкруг вертикальной оси  , проходящей через конец стержня. На стрежень надета пружина закрепленная одним концом в точке О, на другой конец которой надет маленький шарик, массой m (см. рис. 1). При вращении пружина растянется на некоторую величину, при этом на шарик будет действовать сила упругости
, проходящей через конец стержня. На стрежень надета пружина закрепленная одним концом в точке О, на другой конец которой надет маленький шарик, массой m (см. рис. 1). При вращении пружина растянется на некоторую величину, при этом на шарик будет действовать сила упругости  , которая согласно второму закону Ньютона будет равна
, которая согласно второму закону Ньютона будет равна
 ,
,
где R – радиус-вектор, проведенный из начала координат инерциальной системы отсчета 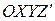 в центр шарика. В системе отсчета
в центр шарика. В системе отсчета  , связанной со стрежнем шарик покоится. Однако сила
, связанной со стрежнем шарик покоится. Однако сила  очевидно будет действовать на него и в этой системе отсчета. Нахождение шарика в состоянии покоя можно формально объяснить, введя силу инерции
очевидно будет действовать на него и в этой системе отсчета. Нахождение шарика в состоянии покоя можно формально объяснить, введя силу инерции
 , (7)
, (7)
направленную противоположно силе упругости вдоль стержня. Такую силу, возникающую в системе отсчета, вращающейся относительно инерциальной системы отсчета, называют центробежной силой инерции.
Элементы специальной теории относительности (СТО).
1. Механический принцип относительности Галилея. Рассмотрим две инерциальные системы отсчета К и К', движущиеся друг относительно друга со скоростью 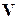 . Условимся, что система К покоится, а система К' движется относительно нее со скоростью
. Условимся, что система К покоится, а система К' движется относительно нее со скоростью 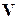 в некотором направлении (см. рис. 2). Принцип преобразования скоростей Галилея основан на двух аксиомах:
в некотором направлении (см. рис. 2). Принцип преобразования скоростей Галилея основан на двух аксиомах:

1) величина временного интервала между двумя событиями инвариантна (не зависит) от выбора инерциальной системы отсчета, иначе говоря скорость течения времени одинакова во всех инерциальных системах отсчета;
2) расстояние между двумя точками инвариантно относительно любой инерциальной системы отсчета.
Основываясь на этих принципах из рис. 2 легко видеть, что
 .
.
Дифференцируя данное соотношение по времени, найдем
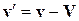 . (8)
. (8)
Соотношение (8) выражает в математической форме принцип преобразования скоростей Галилея.
Заметим, что второй и третий законы Ньютона оказываются инвариантными относительно инерциальных систем отсчета. Таким образом, в классической ньютоновской механике справедлив механический принцип относительности (принцип относительности Галилея): законы механики инвариантны относительно инерциальных систем отсчета.
2. Постулаты и основные соотношения специальной теории относительности. В основу специальной теории относительности, разработанной Эйнштейном, положены два постулата, которые являются обобщением экспериментально установленных закономерностей.
Постулат первый (принцип относительности Эйнштейна): в любых инерциальных системах отсчета все физические явления при одних и тех же условиях протекают одинаково.
Постулат второй (принцип инвариантности скорости света): скорость света в вакууме одинакова во всех инерциальных системах отсчета и не зависит от движения источников и приемников света.
3. Преобразования Лоренца. Из постулатов специальной теории относительности, а также из однородности и изотропности пространства и однородности времени следует, что связь между координатами и временем в двух инерциальных системах отсчета К и К' будет описываться не преобразованиями Галилея, а преобразованиями Лоренца. Для простоты изложения примем, что система К' движется относительно системы К только вдоль оси ОХ, т.е. скорость V системы К' совпадает по направлению с этой осью. Тогда преобразование координат точки М из системы К в систему К' имеет вид
 , (9)
, (9)
 . (10)
. (10)
Преобразование для времени будет иметь вид
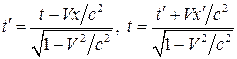 . (11)
. (11)
4. Относительность длин и промежутков времени. Из полученных соотношений вытекает, что интервалы времени между одними и теми же событиями, а также расстояния между двумя точками в двух инерциальных системах отсчета различны. Действительно из (9) и (10) следует, что
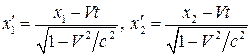
и
 .
.
Введя обозначения 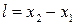 и
и  , получим
, получим
 .
.
Таким образом, для наблюдателя, находящегося в системе отсчета К, расстояние между двумя точками, движущимися относительно этой системы со скоростью V, будет видеться меньшим, чем для наблюдателя в системе К', относительно которого эти точки покоятся. В таком случае говорят, что происходит релятивистское сокращение длины.
Анализируя соотношение (11) можно заметить, что
 .
.
Вводя обозначения 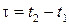 и
и  , получим
, получим
 .
.
Таким образом, в условно неподвижной системе отсчета К промежуток времени между двумя событиями оказывается больше, чем в системе К'. при этом для наблюдателя в системе К' скорость течения времени как бы замедляется (по отношению к наблюдателю в системе К). В таком случае говорят о релятивистском замедлении хода времени.
5. Преобразование скоростей. Получим на основе (9) – (11) соотношения для скоростей движения точки в системах К и К'. По определению
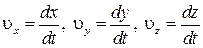 ,
,
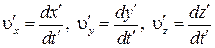 .
.
Заметим, кроме того, что
 .
.
Проводя дифференцирование, получим
 , (12)
, (12)
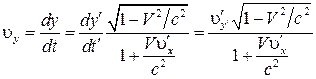 , (13)
, (13)
 . (14)
. (14)
Действуя аналогично, получим
 , (15)
, (15)
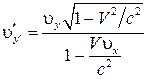 , (16)
, (16)
 . (17)
. (17)
Релятивистские выражения для импульса и кинетической энергии. Энергия покоя. Уравнения Ньютона оказываются не инвариантными относительно преобразований Лоренца. Релятивистское выражение для импульса частицы, движущейся со скоростью 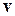 принимает вид
принимает вид
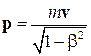 , (18)
, (18)
где 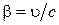 . Выражению (18) можно придать классический вид:
. Выражению (18) можно придать классический вид:
 .
.
Величины  и
и  называют релятивистской массой и массой покоя соответственно.
называют релятивистской массой и массой покоя соответственно.
Выражение для кинетической энергии тела получим из следующих соображений. Запишем второй закон Ньютона:
 .
.
Умножим это соотношение слева на  , а справа на
, а справа на  , получим
, получим
 .
.
Как мы уже установили, работа внешних сил над телом, затрачивается на изменение его кинетической энергии  . Перепишем левую часть полученного соотношения в виде
. Перепишем левую часть полученного соотношения в виде
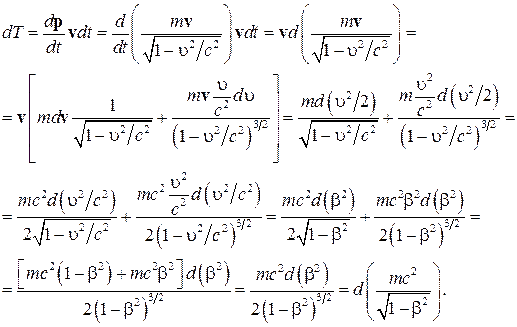
Проинтегрировав последнее соотношение, получим
 . (19)
. (19)
Для нахождения константы используем условие 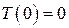 , получим
, получим
 ,
,
откуда 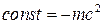 . Тогда соотношение (19) принимает вид
. Тогда соотношение (19) принимает вид
 . (20)
. (20)
Анализ выражения (20) применительно к системе из N взаимодействующих частиц в отсутствие силового поля, показывает, что сумма кинетических энергий частиц не остается постоянной. Этот факт указывает на то, что в отсутствие потенциальных сил выражение (20) не является эквивалентным полной энергии частицы 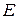 . Можно показать, что выражение для полной энергии частицы должно записываться в виде
. Можно показать, что выражение для полной энергии частицы должно записываться в виде
 . (21)
. (21)
Входящая в (21) величина  называется энергией покоя частицы.
называется энергией покоя частицы.
Соотношение (21) можно также записать в форме
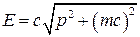 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 1166; Нарушение авторских прав?; Мы поможем в написании вашей работы!