Условные законы распределения. В книге «Представление и использование знаний» (стр.140 ) рассматривается система логического вывода

ИСЧИСЛЕНИЕ ПРЕДИКАТОВ (ГЕНЦЕНА)

В книге «Представление и использование знаний» (стр.140) рассматривается система логического вывода, создателем которой является Г. Генцен (нем. Logische Kalkul).

В этой системе одна аксиома С |– С и 19 правил вывода. В правиле вывода из секвенции (или двух), записанных над чертой выводится секвенция, записанная под чертой. Свойство правила заключается в том, что если справедлива верхняя секвенция, то справедлива и нижняя секвенция.

Секвенция является аналогом теоремы.

A₁, A₂,.., A_m |– B₁,.., B_n

Левая часть секвенции (A₁, A₂,.., A_m) описывает условие теоремы и

называется антецедентом, а правая часть (B₁,.., B_n) – сукцедентом. Смысл секвенции в том, что если выполняется A₁ и... и A_m, то справедливо B₁ или... или B_n.

Если m = 0, то сукцедент считается истиной, при n = 0 антецедент считается ложью (набор формул противоречив).

Антецедент - лат. antecedens (предшествующий, предыдущий).

Консеквент - лат. consequens (следствие, последующий вывод).

Сукцедент - лат. (сукцессия - последовательность)

Правила, в которые входят символы кванторов общности и существования нуждаются в пояснении. Начнем его с правил ® 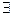и ®. В этих правилах х - переменная, a t- терм. Таким образом A(t) есть результат подстановки t в х.

Пример. Рассмотрим формулу

р(х, у) & x(q(x, z) V r(z, x))

В этой формуле четыре раза появляется переменная х. При этом переменная х, стоящая в формуле со второй по четвертую позиции, является связанной, потому что она присутствует в кванторе общности. А вот первая переменная х является свободной. В этой формуле имеются еще две свободные переменные - это у и z. Результат подстановки терма на место свободной переменной также является формулой. Если вместо свободной переменной z подставить терм (функциональный символ) f(u), то формула примет следующий вид:

р(х, у) & x(q(x, f(u)) V r(f(u), x)

Однако не каждый терм можно подставлять вместо свободной переменной. Например, рассмотрим формулу

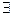x(Øeq(y,x)).

Существует х не равный у. В этой формуле х - связанная переменная, а у - свободная. При замене у на х получим

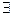x(Øeq(x,x)),

а это уже неправильная формула (существует х не равный х). Следовательно, нельзя производить подстановку, в результате которой свободная переменная, вместо которой подставляется терм, превращается в связанную. Другими словами, среди всех свободных переменных, вместо которых подставляется терм t, в результате подстановки не должно возникнуть ни одной связанной переменной.

Рассмотрим теперь правила 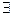® и ® . В этих правилах u – переменная, а А(u) – результат подстановки u вместо х в формуле А(х). При этом переменная u не появляется в нижней секвенции правила и называется собственной переменной правила вывода. Обратим внимание на возможные нарушения при определении собственной переменной. Пусть lt(x, у) интерпретируется как «х меньше, чем у». Тогда применяя вышеуказанные правила, получаем следующий вывод:

eq(u,1) |– lt(0, u)eq(u,1) |– lt(0, u)

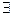x eq(x,1) |– lt(0, u) eq(u,l) |– x lt(0, х)

В данном случае правильной является только верхняя секвенция, так как переменная и осталась в нижней секвенции, а этого быть не должно.

Для дискретных величин были введены условные вероятности по формулам

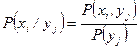и .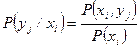

Для непрерывных величин аналогично вводятся плотности для условных законов распределения

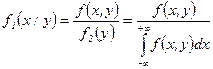и .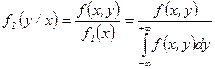

Числовые характеристики составляющих 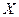и двумерной случайной величины можно найти по формулам

,

,

,

.

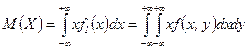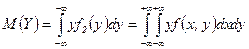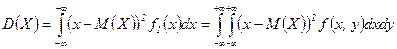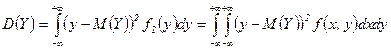Аналогичные характеристики можно ввести и для условных распределений, например, условные математические ожидания

, .

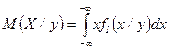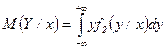Условное математическое ожидание 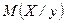будет функцией от :

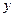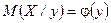, (1)

и наоборот, условное математическое ожидание 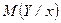будет функцией от:

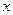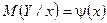. (2)

Функции (1) и (2) называются функциями регрессии: (1) − 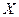на , а (2) − на 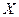. Графики этих функций называются линиями регрессии или кривыми регрессии.

Дата добавления: 2014-01-07