
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Ковариация (корреляционный момент) и коэффициент корреляции
|
|
|
|
Для двумерной случайной величины  характеристики ее составляющих
характеристики ее составляющих 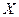 и
и 
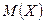 ,
, 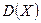 ,
, 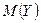 ,
, 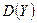 никак не отражают зависимости между
никак не отражают зависимости между 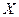 и
и  или ее отсутствия. Поэтому вводится еще одна числовая характеристика − корреляционный момент или ковариация.
или ее отсутствия. Поэтому вводится еще одна числовая характеристика − корреляционный момент или ковариация.
Определение. Ковариацией или корреляционным моментом  случайных величин
случайных величин 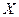 и
и  называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:
называется математическое ожидание произведения отклонений этих величин от их математических ожиданий:
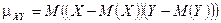 .
.
Используя формулы для математических ожиданий, получаем
для дискретных величин 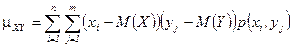 ,
,
для непрерывных величин  .
.
Ковариация характеризует зависимость величин.
Свойства корреляционного момента
1. Для независимых случайных величин 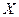 и
и 
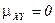 .
.
2. Если 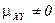 , то случайные величины
, то случайные величины 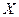 и
и  зависимы.
зависимы.
3. 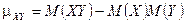 . (Для доказательства достаточно раскрыть скобки под знаком математического ожидания в определении.) В частности
. (Для доказательства достаточно раскрыть скобки под знаком математического ожидания в определении.) В частности
для дискретных величин 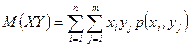 ,
,
для непрерывных величин 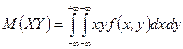 .
.
4. 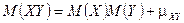 . (Свойство сразу вытекает из 3.)
. (Свойство сразу вытекает из 3.)
5. 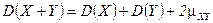 . (Выразите дисперсию через математические ожидания.)
. (Выразите дисперсию через математические ожидания.)
6. 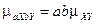 .
.
7. 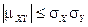 . (Доказательство этого свойства можно найти в [1, гл.14, § 17].)
. (Доказательство этого свойства можно найти в [1, гл.14, § 17].)
Ковариация имеет размерность произведения размерностей случайных величин 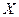 и
и  и зависит от того, в каких единицах измерялись величины. Для получения безразмерной характеристики вводится понятие коэффициента корреляции.
и зависит от того, в каких единицах измерялись величины. Для получения безразмерной характеристики вводится понятие коэффициента корреляции.
Определение. Коэффициентом корреляции 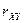 случайных величин
случайных величин 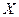 и
и  называется отношение корреляционного момента к произведению средних квадратических отклонений этих случайных величин:
называется отношение корреляционного момента к произведению средних квадратических отклонений этих случайных величин:
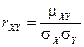 .
.
Свойства коэффициента корреляции
1. Для независимых случайных величин 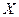 и
и 
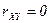 .
.
2. 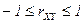 . Коэффициент корреляции по абсолютной величине не превосходит единицы.
. Коэффициент корреляции по абсолютной величине не превосходит единицы.
3. Если 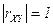 , то случайные величины
, то случайные величины 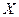 и
и  связаны линейной зависимостью, т.е.
связаны линейной зависимостью, т.е. 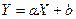 .
.
Определение. Случайные величины 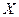 и
и  называются некоррелированными, если
называются некоррелированными, если 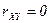 , и коррелированными, если
, и коррелированными, если 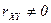 .
.
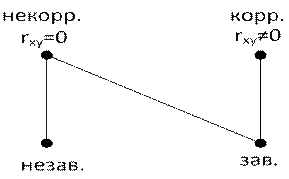
Следует помнить, что понятия некоррелированности и независимости не совпадают, несмотря на внешнее сходство. Независимые величины − некоррелированные, но обратное неверно. Коррелированные величины − зависимые, но обратное неверно. Любые коррелированные величины всегда зависимые, любые независимые величины всегда некоррелированные. Это можно отразить на двудольном графе.
Пример. У случайных величин 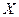 и
и 
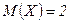 ,
, 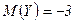 ,
, 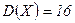 ,
, 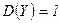 ,
, 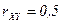 . Найдите
. Найдите 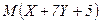 и
и 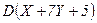 .
.
Решение. 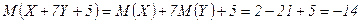 .
.
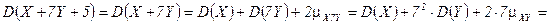
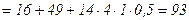 .
.
Ответ. 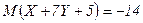 ,
, 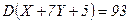 .
.
В заключение рассмотрим пример на вычисление всех характеристик системы случайных величин. Этот же пример рассмотрен в заданиях 6. СИСТЕМЫ СЛУЧАЙНЫХ ВЕЛИЧИН.
Пример. Задан закон распределения системы случайных величин  :
:
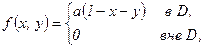
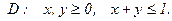
Найдите значение параметра 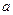 . Найдите законы распределения составляющих
. Найдите законы распределения составляющих 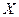 и
и  . Найдите условные законы распределения составляющих. Найдите
. Найдите условные законы распределения составляющих. Найдите 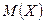 ,
, 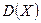 ,
, 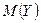 ,
, 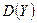 ,
, 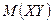 ,
,  ,
, 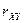 .
.
Решение. а) Согласно свойству 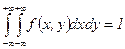 совместной плотности вероятности
совместной плотности вероятности 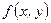 системы случайных величин
системы случайных величин  (свойство 4 из §10) для заданной плотности также
(свойство 4 из §10) для заданной плотности также
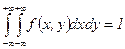 , т.е.
, т.е. 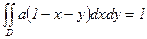 . Вычислим интеграл:
. Вычислим интеграл:
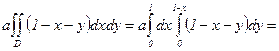
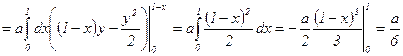 . Следовательно,
. Следовательно, 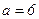 .
.
Итак, плотность вероятности имеет вид
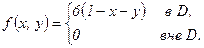
б) Законы распределения составляющих 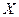 и
и  найдем по формулам:
найдем по формулам:
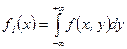 − плотность вероятности составляющей
− плотность вероятности составляющей 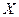 и
и
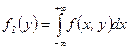 − плотность вероятности составляющей
− плотность вероятности составляющей  .
.
Если 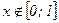 , то
, то 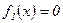 , а при
, а при 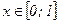
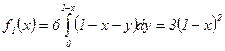 , поэтому
, поэтому
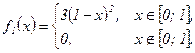
Аналогично, если 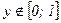 , то
, то 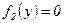 , а при
, а при 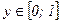
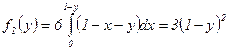 , поэтому
, поэтому
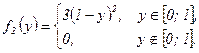
в) Условные законы распределения составляющих 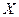 и
и  найдем по формулам:
найдем по формулам:
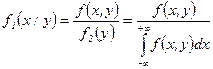 и
и 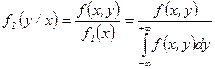 .
.
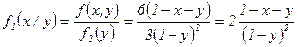 при
при 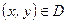 , т.е.
, т.е.
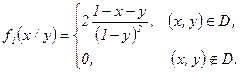
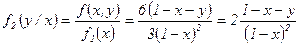 при
при 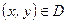 , т.е.
, т.е.
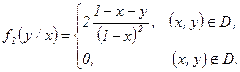
г) Математическое ожидание 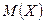 найдем по формуле
найдем по формуле
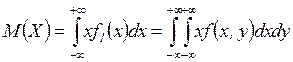 , а т.к.
, а т.к. 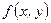 отлична от 0 только в области
отлична от 0 только в области 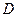 , то
, то
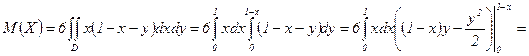
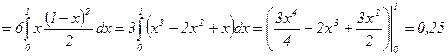 .
.
Аналогично, 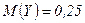 .
.
Для вычисления дисперсии найдем 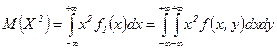 . А т.к.
. А т.к. 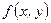 отлична от 0 только в области
отлична от 0 только в области 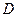 , то
, то
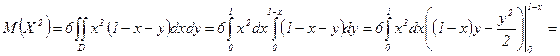
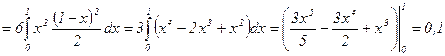 .
.
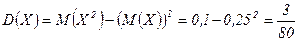 .
.
Аналогичные вычисления для  дают
дают 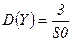 .
.
Средние квадратические отклонения 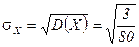 и
и 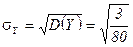 .
.
д) Математическое ожидание 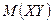 найдем по формуле
найдем по формуле
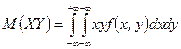 . А т.к.
. А т.к. 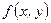 отлична от 0 только в области
отлична от 0 только в области 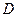 , то
, то
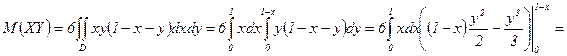
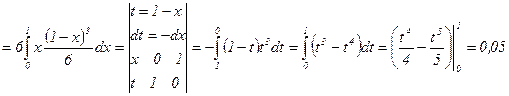 .
.
е) Корреляционный момент  найдем по формуле
найдем по формуле 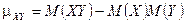 .
.
 .
.
Коэффициент корреляции 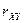 вычисляется по формуле
вычисляется по формуле 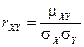 .
.
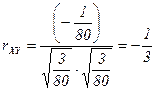 .
.
Так как коэффициент корреляции отличен от 0, случайные величины 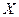 и
и  коррелированные, а значит, зависимые.
коррелированные, а значит, зависимые.
Ответ. 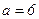 ,
,
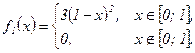 ,
,
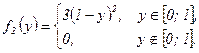
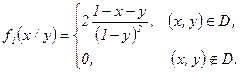
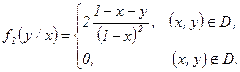
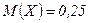 ,
, 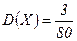 ,
, 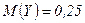 ,
, 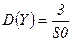 ,
,
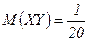 ,
, 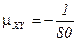 ,
, 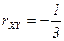 .
.
Замечание. Симметричные значения для составляющих в данном примере получились благодаря симметричности плотности совместного распределения и области 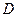 . В общем случае таких совпадений не будет.
. В общем случае таких совпадений не будет.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3658; Нарушение авторских прав?; Мы поможем в написании вашей работы!