
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Лекция 10 . Теоремы о среднем для производных
|
|
|
|
П.1 Локальный экстремум функции.
ОПР. Точка 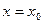 называется точкой локального максимума функции
называется точкой локального максимума функции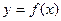 , определенной в некоторой окрестности
, определенной в некоторой окрестности 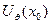 , если
, если  . Если неравенство строгое для всех
. Если неравенство строгое для всех 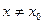 , то говорят о строгом локальном максимуме.
, то говорят о строгом локальном максимуме.
ОПР. Точка 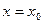 называется точкой локального минимума функции
называется точкой локального минимума функции 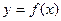 , определенной в некоторой окрестности
, определенной в некоторой окрестности 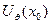 , если
, если 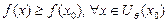 . Если неравенство строгое для всех
. Если неравенство строгое для всех 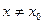 , то говорят о строгом локальном минимуме. Если функция имеет в точке
, то говорят о строгом локальном минимуме. Если функция имеет в точке 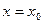 локальный минимум или локальный максимум, то говорят о локальном экстремуме функции.
локальный минимум или локальный максимум, то говорят о локальном экстремуме функции.
ПРИМЕР 1.(не характерный)
Функция  имеет, по определению, в точке
имеет, по определению, в точке 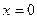 строгий локальный максимум, поскольку
строгий локальный максимум, поскольку 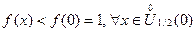 , не смотря на то, что убывает в левосторонней окрестности и возрастает в правосторонней окрестности точки
, не смотря на то, что убывает в левосторонней окрестности и возрастает в правосторонней окрестности точки 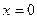 . Следующая теорема устанавливает необходимые условия локального экстремума.
. Следующая теорема устанавливает необходимые условия локального экстремума.
ТЕОРЕМА 1. (Ферма)
Если функция 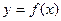 в точке
в точке 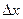 имеет локальный экстремум, то либо функция не имеет производную в точке
имеет локальный экстремум, то либо функция не имеет производную в точке 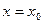 , либо эта производная равна нулю.
, либо эта производная равна нулю.
ДОК. (1) Если производной в точке 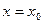 нет, то теорема доказана (см. пример 1). (2) Пусть производная
нет, то теорема доказана (см. пример 1). (2) Пусть производная 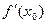 существует и
существует и 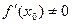 . Тогда
. Тогда 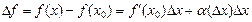
и знак 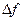 для достаточно малых
для достаточно малых 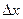 определяется знаком выражения
определяется знаком выражения 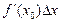 , а он меняется в зависимости от знака
, а он меняется в зависимости от знака 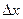 . Последнее противоречит условию локального экстремума в точке
. Последнее противоречит условию локального экстремума в точке 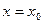 , т.е.
, т.е. 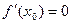 .
.
П.2 Теоремы о среднем для производных.
ТЕОРЕМА 2. (Ролля)
Если функция 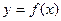 1) непрерывна на отрезке [a;b],
1) непрерывна на отрезке [a;b],
2) дифференцируема в каждой точке интервала (a;b), 3) принимает на концах отрезка равные значения: 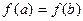 ,
,
то существует на интервале (a;b) такая точка c, для которой  .
.
ДОК. По доказанной теореме непрерывная на [a;b] функция принимает на этом отрезке наибольшее и наименьшее значения: 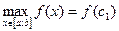 и
и 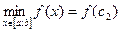 . Если одна из точек c1 или c2 лежит на интервале (a,b), то теорема доказана, поскольку эта точка является точкой локального экстремума и по теореме 1
. Если одна из точек c1 или c2 лежит на интервале (a,b), то теорема доказана, поскольку эта точка является точкой локального экстремума и по теореме 1  . Если
. Если 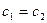 или
или 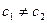 , но они совпадают с концами отрезка, то
, но они совпадают с концами отрезка, то 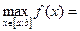
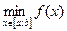 и функция постоянная на отрезке[a;b] и
и функция постоянная на отрезке[a;b] и  .
.
ПРИМЕР 2. Функция 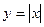 на отрезке
на отрезке 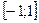 удовлетворяет всем условиям теоремы Ролля, кроме одного: в точке
удовлетворяет всем условиям теоремы Ролля, кроме одного: в точке 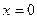 функция не имеет производную. При этом утверждение теоремы не выполняется:
функция не имеет производную. При этом утверждение теоремы не выполняется: 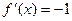 для
для 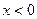 и
и 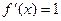 для
для 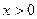 .
.
ТЕОРЕМА 3. (Коши)
Если функции 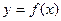 и
и 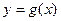 1) непрерывны на отрезке [a;b], 2) дифференцируемы в каждой точке интервала (a;b), 3)
1) непрерывны на отрезке [a;b], 2) дифференцируемы в каждой точке интервала (a;b), 3) 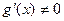 на интервале
на интервале 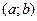 ,
,
то существует на интервале (a;b) такая точка c, для которой
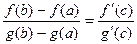 .
.
ДОК. Из условия теоремы следует, что  . Действительно, если
. Действительно, если  , то функция
, то функция 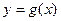 удовлетворяет условиям теоремы Ролля и тогда найдется такая точка c, для которой
удовлетворяет условиям теоремы Ролля и тогда найдется такая точка c, для которой 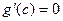 , что противоречит условию 3) теоремы. Рассмотрим вспомогательную функцию
, что противоречит условию 3) теоремы. Рассмотрим вспомогательную функцию 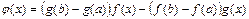 .
.
Проверим, что 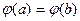 . Действительно,
. Действительно, 
и функция 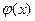 удовлетворяет условию теоремы Ролля. Тогда найдется
удовлетворяет условию теоремы Ролля. Тогда найдется 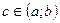 , для которой
, для которой
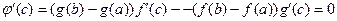 .
.
Из последнего равенства следует утверждение теоремы.
ТЕОРЕМА 4 (Лагранжа)
Если функции 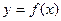 1) непрерывна на отрезке [a;b],
1) непрерывна на отрезке [a;b],
2) дифференцируема в каждой точке интервала (a;b), то существует на интервале (a;b) такая точка c, для которой
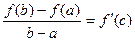 .
.
ДОК. Следует из теоремы Коши для 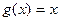 .
.
П.3 Следствия из теорем о среднем.
ТЕОРЕМА 5. (правило Лопиталя для раскрытия неопределенности 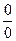 )
)
Если функции 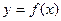 и
и 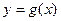 1) непрерывны на [a;b), (а и b не обязательно конечны), 2) дифференцируемы в каждой точке интервала (a;b), 3)
1) непрерывны на [a;b), (а и b не обязательно конечны), 2) дифференцируемы в каждой точке интервала (a;b), 3)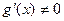 на интервале
на интервале 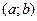 ,
,
4) 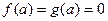 , 5) существует
, 5) существует 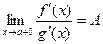 ,
,
то существует 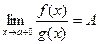 .
.
ДОК. Для любого 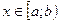 на отрезке
на отрезке  выполняются условия теоремы Коши и найдется
выполняются условия теоремы Коши и найдется 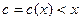 , для которого
, для которого 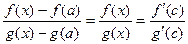 .Если
.Если 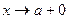 , то
, то 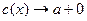 и
и 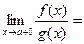
 =
=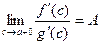 .
.
В теореме допускается случай 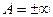 .
.
ТЕОРЕМА 6. (правило Лопиталя для раскрытия неопределенности 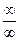 )
)
Если функции 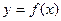 и
и 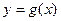 1) непрерывны на [a;b), (а и b не обязательно конечны), 2) дифференцируемы в каждой точке интервала (a;b), 3)
1) непрерывны на [a;b), (а и b не обязательно конечны), 2) дифференцируемы в каждой точке интервала (a;b), 3) 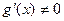 на интервале
на интервале 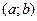 ,
,
4) 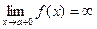 ,
,  ,5) существует
,5) существует 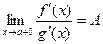 .,
.,
то существует 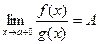 .
.
ДОК. (1) Пусть А – конечное число. Тогда  .Определим функцию
.Определим функцию 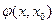 из условия
из условия 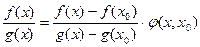 , т.е.
, т.е.
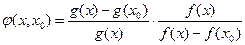 Заметим, что
Заметим, что 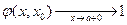 .(условие 5)) Применим для отрезка
.(условие 5)) Применим для отрезка  и функций
и функций 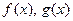 теорему Коши. Тогда для некоторой точки
теорему Коши. Тогда для некоторой точки 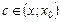 :
: 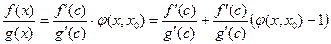
и для всех x, для которых 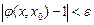 имеем
имеем 
т.е.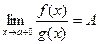 .
.
(2) Пусть 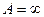 . Тогда
. Тогда 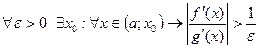 .
.
Если x достаточно близок к a, то из  следует
следует 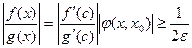 и
и 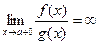 .
.
УПРАЖНЕНИЯ 1) Пусть 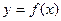 определена на отрезке
определена на отрезке 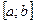 и при любых
и при любых 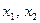 из этого отрезка выполняется неравенство:
из этого отрезка выполняется неравенство:  ,
, 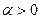 . Доказать, что функция
. Доказать, что функция 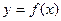 постоянная.
постоянная.
ВОПРОСЫ К ЭКЗАМЕНУ.
1) Локальный экстремум функции, теорема Ферма.
2) Теоремы о среднем для производных. Теорема Ролля.
3) Теоремы о среднем для производных. Теорема Коши.
4) Теоремы о среднем для производных. Теорема Лагранжа. Теорема Лопиталя для раскрытия неопределенностей 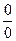 .
.
5) Теорема Лопиталя для раскрытия неопределенностей 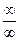 .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 648; Нарушение авторских прав?; Мы поможем в написании вашей работы!