Лекция 12 . Формула Тейлора 2

П.1 Формула Тейлора с остаточным членом в форме Лагранжа.

ТЕОРЕМА 1. (обобщенная теорема Коши)

Пусть даны функции 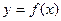, , 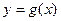определенные на отрезке 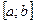, имеющие непрерывные производные до порядка 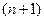на интервале 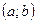, причем

1) 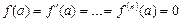(производные в точке a правые)

2) ,

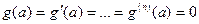3) 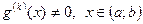, для .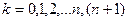

Тогда существует 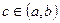, для которого .

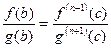ДОК. Применим последовательно теорему Коши: существует :.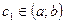

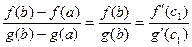На отрезке 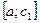выполняются условия теоремы Коши и существует 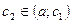, для которого 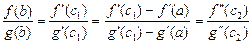. Продолжая, на отрезке 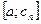существует точка 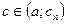, для которого .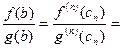

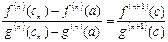ТЕОРЕМА 2. (формула Тейлора с остаточным членом в форме Лагранжа)

Пусть функция 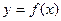непрерывна и имеет непрерывные производные до (n+ 1) порядка на конечном отрезке 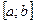. Тогда существует 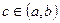, для которого 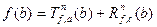, где 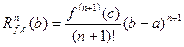(остаточный член в форме Лагранжа).

ДОК. Применим обобщенную теорему Коши для функци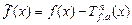й и 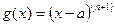. Условия теоремы проверялись для функции 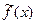(см. пример) и очевидны для функции 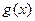. Тогда существует точка 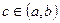, для которой

.

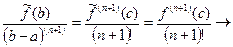
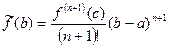П.2 Интервалы монотонности.

ОПР. Функция возрастает в точке 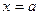, если для любых достаточно малых 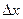, т.е. положительным приращениям аргумента соответствуют положительные приращения функции и уменьшению аргумента (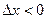) соответствует уменьшение значения функции ().

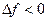ОПР. Функция убывает в точке 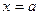, если 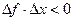для любых достаточно малых 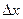, т.е. положительным приращениям аргумента соответствуют отрицательные приращения функции и уменьшению аргумента (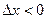) соответствует увеличения значения функции ().

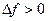ОПР. Интервал 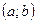называется интервалом возрастания (убывания) функции 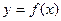,если каждая его внутренняя точка является точкой возрастания (убывания) функции.

ТЕОРЕМА 3. (ДОСТАТОЧНЫЕ УСЛОВИЯ МОНОТОННОСТИ функции на интервале)

Пусть функция 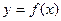дифференцируема на интервале 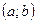и 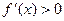(),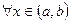. Тогда функция 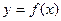строго возрастает (убывает) на интервале .

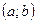ДОК. (1) Пусть 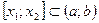. Тогда по теореме о среднем Лагранжа существует 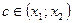, для которого .

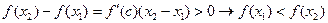(2) для убывания по аналогии.

Таким образом, интервалы монотонности функции совпадают с интервалами знакопостоянства ее производной. Для их нахождения необходимо найти производную функции, приравнять ее нулю и найти точки из области определения функции, в которых производная равна нулю или не существует. Эти точки, называемые критическими, являются границами интервалов монотонности. Если на одном из них производная 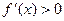, то это интервал возрастания функции, в противном – интервал убывания. Точка, в которой 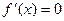, может служить границей противоположных интервалов монотонности или, например, двух интервалов возрастания, которые можно объединить в один.

ПРИМЕР 1. Функция 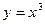строго возрастает на R, но имеет точку 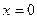критической.

П.3. Экстремумы функции. Необходимые и достаточные условия.

Понятия локального экстремума (максимума или минимума) можно сформулировать в терминах приращения функции: функция 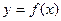имеет в точке 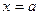строгий локальный максимум, если ее приращение 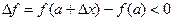для любых достаточно малых 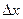. Для локального минимума знак неравенства противоположный. Для не строгого локального максимума знаки неравенства не строгие.

ТЕОРЕМА 4.(НЕОБХОДИМОЕ УСЛОВИЕ ЭКСТРЕМУМА)

Пусть в точке 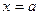функция 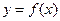имеет локальный экстремум. Тогда либо 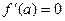, либо производной в точке 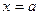не существует.

ДОК. (1) для максимума. Если производной в точке 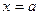нет, то теорема доказана. Если производная существует, то 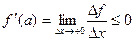и 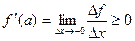, т.е. .

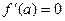(2) для минимума (по аналогии).

ПРИМЕР 2. Функция 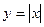имеет в точке 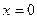строгий локальный минимум, хотя в точке 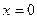производной у функции нет.

ТЕОРЕМА 5. (ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА по первой производной)

Пусть точка a является границей двух интервалов монотонност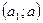и и 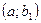, функция 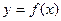непрерывна в точке 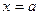, причем

(1) интервал 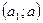является интервалом возрастания, а 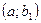- интервалом убывания функции. Тогда в точке 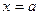функция имеет локальный максимум.

(2) интервал 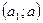является интервалом убывания, а 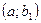- интервалом возрастания функции. Тогда в точке 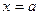функция имеет локальный минимум.

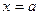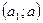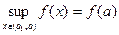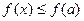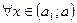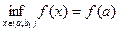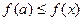ДОК. (1) Из непрерывности функции в точке и монотонного роста функции на интервалеследует, что и для . Аналогично, и для 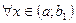. Тогда 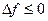для достаточно малых 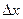. Если предположить строгую монотонность на интервалах 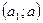и 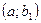, то экстремум будет строгим.

ТЕОРЕМА 6. (ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА по второй производной)

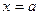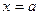Если точка критическая и существует , то в точке функция имеет локальный минимум, если 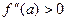, и локальный максимум, если .

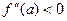ДОК. Заметим, что в условиях теоремы 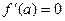. Разложим функцию 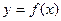по формуле Тейлора в окрестности точки :

.

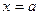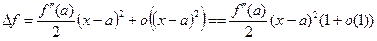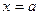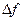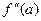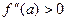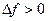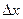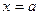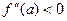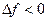Тогда в малой окрестности точки , приращение сохраняет знак производной . Если , то для достаточно малых значений , т.е. в точке локальный минимум. Если , то для достаточно малых 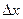и в точке 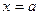- локальный максимум. Последняя теорема обобщается на случай производных более высоких порядков.

ТЕОРЕМА 7. (ДОСТАТОЧНОЕ УСЛОВИЕ ЭКСТРЕМУМА по производной четного порядка)

Если в точке 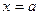производные , ,

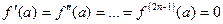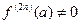то в точке 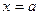функция имеет локальный минимум, если 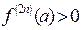и максимум, если .

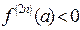ДОК. Воспользуемся формулой Тейлора: 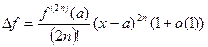. Тогда знак приращения 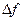определяется знаком производной .

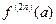УПРАЖНЕНИЕ. Каково поведение функции в окрестности точки 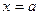, если

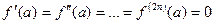, а ?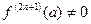

ВОПРОСЫ К ЭКЗАМЕНУ.

1) Обобщенная теорема Коши и формула Тейлора с остаточным членом в форме Лагранжа.

2) Возрастание функции в точке и на интервале. Теорема о достаточном условии возрастания функции на интервале. Нахождение интервалов монотонности.

3) Локальный экстремум функции. Необходимое условие экстремума. Достаточное условие экстремума по первой производной.

4) Достаточное условие экстремума по второй производной и четной производной.

Дата добавления: 2014-01-07