Непрерывный спектр стационарной случайной функции

Среди стационарных случайных функций есть такие функции, корреляционные функции которых нельзя представить в виде 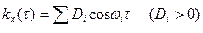, где число слагаемых конечно или счетно. Спектр этих функций не дискретный, а непрерывный. Для рассмотрения стационарных случайных функций с непрерывным спектром необходимо ввести понятия спектр плотности.

Пусть в варианте Б п. 2.1 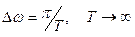, тогда 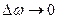. Ясно, что при этом частота изменяется непрерывно (поэтому обозначим ее через w без индекса), соседние ординаты спектра сближаются и в пределе вместо дискретного спектра получим непрерывный спектр, то есть каждой частоте 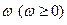соответствует ордината, которую обозначим через .

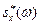Хотя отрицательные частоты физического смысла не имеют, для упрощения вычислений целесообразно считать, что частоты изменяются в интервале 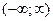, и вместо функции 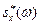рассматривать функцию, которая имеет вдвое меньшие ординаты:

.

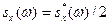Определение 2.3. Спектральной плотностью стационарной случайной функции X(t) называют функцию s_x(w), которая связана с корреляционной функцией k_х(t) взаимно обратными преобразованиями Фурье:

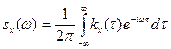, (8)

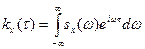. (9)

Эти формулы называются формулами Винера - Хинчина. В действительной форме они представляют собой взаимно обратные косинус преобразования Фурье:

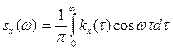(10)

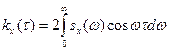(11)

Важное значение спектральной плотности состоит в том, что, зная ее, можно найти корреляционную функцию, и обратно.

Из (10) следует, что спектральная плотность - четная функция:

.

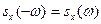Выясним вероятностный смысл функции 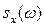. Положив t = 0 в соотношении (11) и учитывая, что 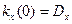, 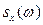- четная функция, получим:

.

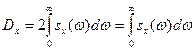Видим, что дисперсия стационарной случайной функции X(t) представляет собой «сумму» элементарных дисперсий 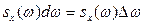, каждая элементарная дисперсия соответствует частичному интервалу частот 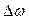. В частности, частичному интервалу 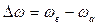соответствует дисперсия

.

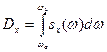По теореме о среднем,

.

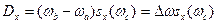где .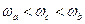

Отсюда

.

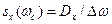Из чего заключаем:

а) величину 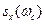можно истолковывать как среднюю плотность дисперсии на частном интервале 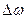, содержащим частоту ;

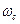б) при 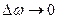естественно считать, что 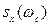- плотность дисперсии в точке 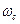. Поскольку никаких ограничений на 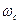не наложено, полученный результат справедлив для любой частоты.

Итак, спектральная плотность описывает распределение дисперсий стационарной случайной функции по непрерывно изменяющейся частоте. Спектральная плотность - неотрицательная функция .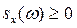

Определение 2.4. Нормированной спектральной плотностью стационарной случайной функции X (t) называют отношение спектральной плотности к дисперсии случайной функции:

.

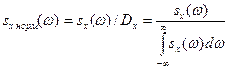Пусть X(t) и У(t) - стационарные и стационарно связанные случайные функции со взаимной корреляционной функцией r_xy(t).

Определение 2.5. Взаимной спектральной плотностью двух стационарных и стационарно связанных случайных функций X(t) и Y(t) называют функцию s_xy(w), определяемую преобразованием Фурье:

.

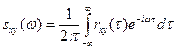В свою очередь, взаимная корреляционная функция выражается через взаимную спектральную плотность с помощью обратного преобразования Фурье:

.

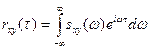2.3. Дельта – функция

Дельта - функция 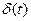является примером обобщенной функции (обобщенная функция - предел последовательности однопараметрического семейства непрерывных функций). Дельта - функцию определяют тем условием, что она ставит в соответствие всякой непрерывной функции f(t) ее значение при t=0:

.

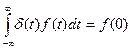Правую часть равенства можно представить в виде:

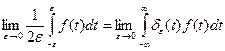(e>0),

где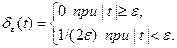

Таким образом, дельта - функцию можно рассматривать как предел последовательности функци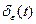и при .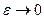

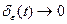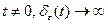Учитывая, что, при , при пр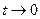и и 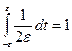, условно пишут

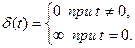
Физически дельта - функцию можно истолковать как плотность единичной массы, сосредоточенной в нуле. Можно доказать, что дельта - функция представима преобразованием Фурье:

.

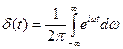Отсюда

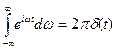. (12)

Дата добавления: 2014-01-07