Дюрация и выпуклость портфеля облигаций

Предположим, что на рынке присутствуют облигации l видов, стоимость которых в данный (нулевой) момент равны соответственно 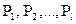. Будем считать, что данные облигации можно покупать в любом количестве.

Инвестор, затратив на покупку сумму 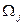на покупку облигаций j -го вида (j = 1,2,3, …, l), сформирует портфель облигаций 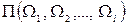стоимостью .

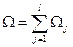Портфель облигаций 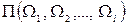эквивалентен облигации стоимостью 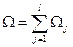, по которой в моменты 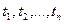должны выплачиваться соответствующие денежные суммы

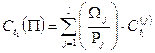
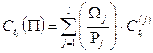
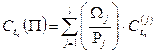
где 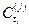- платеж по j-той облигации в момент времени 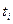(i = 1,2, …, n).

Дюрацией 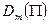и соответственно выпуклостью 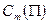портфеля облигаций П при начислении процентов m раз в год называется дюрация и выпуклость облигации, эквивалентной этому портфелю облигаций.

Если r – внутренняя доходность портфеля облигаций П при начислении процентов m раз в год, то

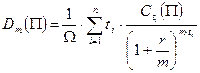[78]

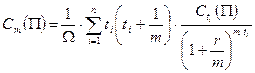[79]

Модифицированная дюрация и выпуклость определяются по формуле:

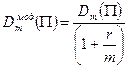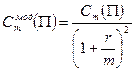, [80]

Относительное изменение стоимости портфеля облигаций при изменении процентных ставок определяется по формуле:

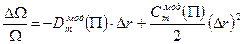[81]

где 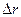- изменение внутренней доходности портфеля облигаций П;

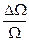- относительно изменение стоимости портфеля облигаций П;

Пример. Временная структура процентных ставок при начислении процентов дважды в год приведена ниже.

Срок, годы	0,5	1,0	1,5	2,0
Безрисковая процентная ставка,%		6,5

Рассмотрим портфель П=П(2000,1000,500) из облигаций, основные характеристики которых приведены в табл. 9.

Таблица 9

Исходные данные

Облигация	Платежи по срокам, долл.
0,5		1,5
А
В
С

Необходимо определить модифицированную дюрацию и выпуклость портфеля облигаций П.

Решение. Сначала необходимо определить рыночную стоимость облигаций, входящих в портфель.

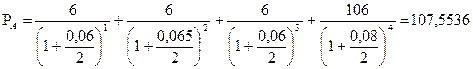
Аналогично получили курсы облигаций В и С, которые составили 110,3743 и 101,5707 долл. соответственно.

Теперь нужно определить поток денежных средств, генерируемый портфелем облигаций П.

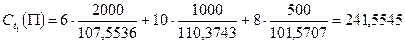
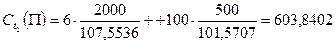
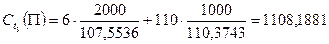
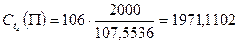
Для нахождения дюрации и выпуклости портфеля облигаций необходимо определить внутреннюю доходность портфеля П. Для этого нужно решить следующее уравнение:

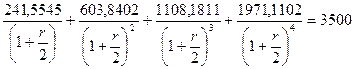
Решив данное уравнение, получаем, внутренняя доходность портфеля облигаций равна 7,264%. Теперь можно найти дюрацию и выпуклость портфеля облигаций П используя формулы [78] и [79].

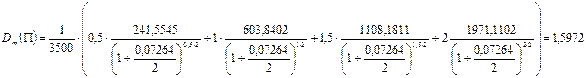
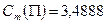
Тогда

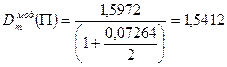
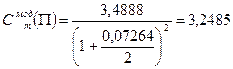
Кроме того, существует понятие средневзвешенной дюрации и выпуклости портфеля облигаций П.

Средневзвешенной дюрацией (средневзвешенной выпуклостью) портфеля облигаций 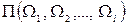называется взвешенная по стоимости сумма модифицированных дюраций (модифицированных выпуклостей) облигаций этого портфеля, т.е.

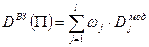[82]

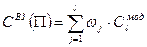[83]

Дата добавления: 2014-01-07