Решение. Симметрическая разность

Симметрическая разность

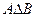– либо А обладает каким-нибудь свойством f, либо В обладает каким-нибудь свойством f, но не оба вместе.

Пример. Записать свойства бинарных отношений при помощи логических связок.

1. Рефлексивность: 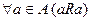. (если 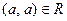для всех )

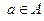2. Антирефлексивность: .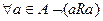

3. Симметричность: .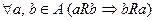

4. Антисимметричность: .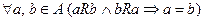

5. Асимметричность: .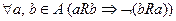

6. Транзитивность: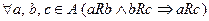

Определение 13. Формула алгебры логики – простые высказывания или сложные, полученные из простых посредством применения конечного числа логических операций.

Свойства логических операций (основные законы алгебры)

1. Коммутативность.

,

,

.

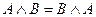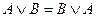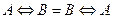2. Ассоциативность.

,

,

.

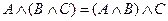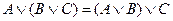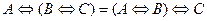Замечание. Свойства 1,2 не выполняются для импликации «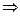», т.е. , .

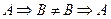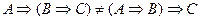3. Дистрибутивность.

,

,

,

.

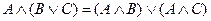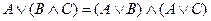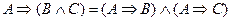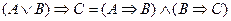4. Отрицание.

,

,

,

.

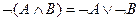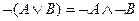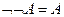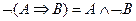5. Импликация.

,

,

.

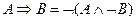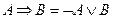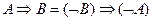Определение 14. Пусть 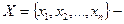множество или предметная область, 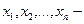предметные переменные. n-местным предикатом, определенным на области X, называют отображение множества Х во множество высказываний. n-местный предикат – это связное повествовательное предложение, содержащее n переменных и обладающее следующим свойством: при фиксации всех переменных о нем (предложении) можно сказать ложно оно или истинно.

Предикат – синоним слова «отношение», т.е. это функция, утверждающая истину или ложь.

Обозначение: Р (x ₁, x ₂,… x_n) или f (x ₁, x ₂,… x_n).

Пример 1. а)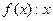– человек – одноместный предикат,

b)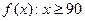– одноместный предикат. 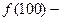истинно, 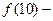ложно.

c) 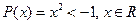– одноместный предикат, при всех х ложный.

d) предикат равенства 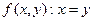. При 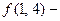ложно, 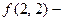истинно. Это двуместный предикат.

е)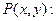натуральное число х делится без остатка на натуральное число y – двуместный предикат на множестве натуральных чисел. 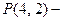истинно, 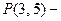ложно.

Пример 2. Даны предикаты: 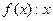– человек; 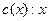– машина; 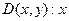ездит на y. Записать утверждения: а) никакой человек не является машиной, b) существует человек, с) только люди водят машины.

Дата добавления: 2014-01-07