Истинность высказываний

Решение.

а) никакой человек не является машиной: .

b) существует человек: .

с) только люди водят машины: .

Определение 15. Высказывание 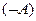истинно, если А ложно.

Определение 16. Высказывание 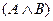– конъюнкция – истинно, если А и В оба истинны, и ложно в противном случае.

Например: высказывание ((2+2=5) 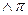-рациональное число) – ложное, т.к. первое высказывание ложное: .

Определение 17. Высказывание 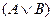– дизъюнкция – истинно, если хотя бы одно из высказываний А и В истинно.

Например: высказывание ((2+2=5) 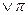-рациональное число) – истинное, т.к. второе высказывание истинное: -рациональное число.

Определение 18. Высказывание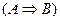– импликация – ложно, если А – истинно, а В – ложно, и истинно во всех других случаях.

Например: Предварительно обозначим: истинно – и, ложно– л.

а) (1+1 = 2) 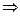(Париж – столица Франции). Высказывание истинно: и 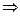и.

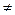b) (1+1 2) 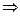(Париж – столица Франции). Высказывание истинно: л 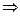и.

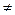с) (1+1 2) 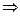(Рим – столица Франции). Высказывание истинно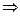: л л.

d) (1+1 = 2) 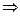(Рим – столица Франции). Высказывание ложно: и 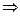л.

Определение 19. Высказывание 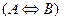истинно, когда А и В оба истинны или оба ложны.

Вывод: Всякое высказывание, построенное при помощи логических связок, имеет некоторое истинностное значение, зависящее от истинностных значений составляющих высказываний.

п. 3. Таблицы истинности.

Определение 20. Пропозициональная форма или формула алгебры высказываний – это выражение, построенное из пропозициональных переменных (высказываний) с помощью логических связок, точнее 1) все высказывания – есть формула, 2) если А и В – формулы, то (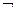 А), (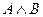), (), (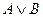), (), (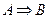) 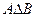– тоже формулы, 3) только те выражения являются формулами, для которых это следует из 1) и 2).

Всякая формула алгебры определяет некоторую истинностную функцию, которая, в свою очередь, определена на множестве { и, л }. Графически формула (т.к. это функция) может быть представлена истинностной таблицей или таблицей истинности для этой формулы.

Определение 21. Таблица истинности – распределение истинностных значений пропозициональных букв (высказываний), входящих в формулу.

Построение таблицы истинности: под всеми вхождениями каждого из высказываний подписываем соответствующие истинностные значения. Каждая строка таблицы содержит некоторое распределение истинностных значений для букв и соответствующие истинностные значения, принимаемые различными формулами, которые возникают при построении окончательной формулы.

Дата добавления: 2014-01-07