
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Пассивный двухполюсник в цепи синусоидального тока. Эквивалентные сопротивления и проводимости
|
|
|
|
На рис. 2.36 показан пассивный двухполюсник, состоящий из активных и реактивных элементов. Действующие значения напряжения  , тока
, тока  и угол сдвига фаз между ними
и угол сдвига фаз между ними  известны.
известны.
 Рис. 2.36. Пассивный двухполюсник
Рис. 2.36. Пассивный двухполюсник
|
Построим по этим значениям векторную диаграмму и, спроектировав вектор напряжения на вектор тока и перпендикулярное к нему направление, получим треугольник напряжений, образованный сторонами 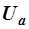 ,
,  и
и  (рис. 2.37, а).
(рис. 2.37, а).
Как и раньше, 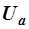 и
и  будем называть активной и реактивной составляющими напряжения. Изображенная в таком виде диаграмма соответствует схеме, показанной на рис. 2.37, б. Действительно, для нее
будем называть активной и реактивной составляющими напряжения. Изображенная в таком виде диаграмма соответствует схеме, показанной на рис. 2.37, б. Действительно, для нее  ,
,  и
и  . Схема называется последовательной схемой замещения или последовательной эквивалентной схемой пассивного двухполюсника, а ее параметры
. Схема называется последовательной схемой замещения или последовательной эквивалентной схемой пассивного двухполюсника, а ее параметры  ,
,  и
и  – эквивалентными сопротивлениями двухполюсника.
– эквивалентными сопротивлениями двухполюсника.

Рис. 2.37. Векторная диаграмма и соответствующая ей последовательная эквивалентная схема
Треугольник, образованный сторонами  ,
,  и
и  и подобный треугольнику напряжений, представляет собой треугольник сопротивлений (рис. 2.28, б), для которого справедливы формулы (2.27).
и подобный треугольнику напряжений, представляет собой треугольник сопротивлений (рис. 2.28, б), для которого справедливы формулы (2.27).
Теперь разложим в е к т о р т о к а на две составляющие – активную  , направленную по вектору напряжения, и реактивную
, направленную по вектору напряжения, и реактивную  , перпендикулярную к нему (рис. 2.38, а). Такой векторной диаграмме соответствует параллельная схема замещения двухполюсника (рис. 2.38, б). Ее параметры
, перпендикулярную к нему (рис. 2.38, а). Такой векторной диаграмме соответствует параллельная схема замещения двухполюсника (рис. 2.38, б). Ее параметры 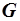 ,
, 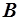 и
и  называются эквивалентными проводимостями. Токи в элементах
называются эквивалентными проводимостями. Токи в элементах 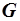 и
и 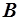 мы и представляем как активную и реактивную составляющие общего тока:
мы и представляем как активную и реактивную составляющие общего тока:  ,
, 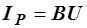 . Из треугольника токов (рис. 2.38, а) получается треугольник проводимостей
. Из треугольника токов (рис. 2.38, а) получается треугольник проводимостей
(рис. 2.32, б), стороны которого связаны между собой формулами (2.29).

а) б)
Рис. 2.38. Параллельная эквивалентная схема и ее векторная диаграмма
Получим условия эквивалентности приведенных схем.
Для последовательной цепи  , для параллельной
, для параллельной  , а так как токи и напряжения в обеих схемах одинаковы, то
, а так как токи и напряжения в обеих схемах одинаковы, то
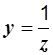 и
и  , (2.30)
, (2.30)
т.е. в любой электрической цепи полная проводимость есть величина, обратная полному сопротивлению.
Из сопоставления формул (2.27) и (2.29) можно записать:
 и
и 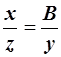 .
.
Рассматривая последние выражения совместно с (2.30), можно получить две группы формул:
| Формулы перехода от последовательной эквивалентной схемы к параллельной: | Формулы перехода от параллельной эквивалентной схемы к последовательной: |
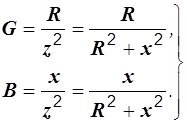 (2.31) (2.31)
|
 (2.32) (2.32)
|
Обращаем внимание на то, что каждая из проводимостей G и B зависит от обоих сопротивлений – активного и реактивного.
В свою очередь, каждое из сопротивлений определяется обеими проводимостями. Соотношения G = 1 /R и B = 1 /x справедливы только в частном случае, первое – при х = 0, второе – при R = 0.
Следует отметить, что активная и реактивная составляющие напряжения и тока физически не существуют, измерить их нельзя. Они относятся только к соответствующим эквивалентным схемам замещения и находятся расчетом. Более того, проектируя, например, вектор тока на различные напряжения, мы получим для него разные составляющие.
Пример 2.15. Найти общее сопротивление цепи, состоящей из параллельно соединенных активного R = 30 Ом и индуктивного
х = 40 Ом сопротивлений (рис. 2.39, а).

Рис. 2.39. Схемы к примерам 2.15–2.17
Р е ш е н и е. Так как в левой ветви реактивного сопротивления нет, то ее проводимость в соответствии с (2.31) равна G = 1 /R. Аналогично, во второй ветви B = 1 /x. Полная проводимость цепи 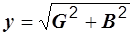 . В соответствии с (2.30) полное сопротивление цепи
. В соответствии с (2.30) полное сопротивление цепи
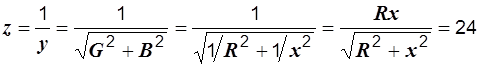 Ом.
Ом.
Пример 2.16. Рассчитать общее сопротивление цепи, состоящей из параллельно соединенных индуктивности L = 0,478 Гн и емкости С = 31,85 мкФ (рис. 2.39, б). Частота питающего напряжения f = 50 Гц.
Р е ш е н и е. Определяем сопротивления ветвей:
 Ом,
Ом,
 Ом.
Ом.
Так как в ветвях отсутствуют активные сопротивления, то их проводимости соответственно равны BL = 1 /xL и BC = 1 /xС. Полная эквивалентная проводимость цепи не содержит активной составляющей и равна
 .
.
Полное эквивалентное сопротивление
 Ом.
Ом.
В рассматриваемой цепи активных элементов нет, она носит чисто реактивный характер. Он может быть индуктивным или емкостным. Знак минус в ответе свидетельствует о последнем, т.е. вся цепь может быть заменена конденсатором емкостью
 мкФ.
мкФ.
Пример 2.17. Амперметр А, вольтметр V и фазометр j, включенные в цепь катушки (рис. 2.39, в), дали следующие показания:
U = 220 В, I = 4,4 А, cos j = 0,8. Частота питающего напряжения
50 Гц. Определить параметры последовательной и параллельной схем замещения катушки.
Р е ш е н и е. Находим параметры последовательной эквивалентной схемы:
 Ом,
Ом,  Ом,
Ом,
 Ом.
Ом.
Рассчитываем элементы параллельной эквивалентной схемы:
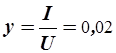 См,
См,  См,
См,
 См.
См.
После определения эквивалентных сопротивлений эквивалентные проводимости можно было найти иначе, по формулам (2.31):
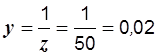 См,
См,  См,
См,
 См.
См.
 Рис. 2.40. Расчетная схема
Рис. 2.40. Расчетная схема
|
Пример 2.18. Рассчитать токи в схеме, приведенной на рис. 2.40.
 В,
В,
 Ом,
Ом,
 Ом,
Ом,
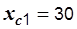 Ом,
Ом,
 Ом,
Ом,
 Ом,
Ом,
 Ом,
Ом,
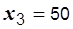 Ом.
Ом.
Р е ш е н и е. Определяем полные сопротивления второй и третьей ветвей:
 Ом,
Ом, 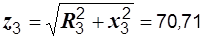 Ом.
Ом.
Преобразуем эти ветви в эквивалентные параллельные
(рис. 2.41, а).

Рис. 2.41. Преобразования электрической цепи
Их проводимости:
 См,
См,  См,
См,
 См,
См,  См.
См.
Суммируем активные и реактивные проводимости параллельных ветвей:  См,
См,  См
См
(см. рис. 2.41, б).
Определяем эквивалентные сопротивления участка 
(рис. 2.41, в):
 Ом,
Ом,  Ом,
Ом,
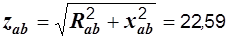 Ом,
Ом,
и полное сопротивление цепи:
 Ом.
Ом.
Ток на входе цепи I1 = U/z = 220/41,53 = 5,297 A.
Напряжение на участке  Uab = I1zab = 119,7 В.
Uab = I1zab = 119,7 В.
Токи второй и третьей ветвей:
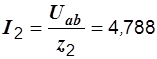 А,
А,  А.
А.
Еще раз напоминаем, что для численных значений токов и напряжений законы Кирхгофа неприменимы:  .
.
|
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 3079; Нарушение авторских прав?; Мы поможем в написании вашей работы!