
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Интегрирование дробно-рациональных функций
|
|
|
|
Интегралы от дробно-рациональных функций встречаются достаточно часто, более того, многие более сложные интегралы сводятся к ним.
Определение 1. Дробно-рациональной функцией называется выражение вида 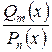 , где числитель и знаменатель – есть многочлены (полиномы), то есть выражения вида
, где числитель и знаменатель – есть многочлены (полиномы), то есть выражения вида
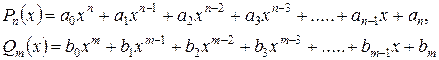 .
.
В некоторых учебных пособиях эти функции называются рациональными функциями или рациональной дробью.
Определение 2. Дробь называется правильной, если старшая степень многочлена, находящегося в числителе, меньше старшей степени многочлена в знаменателе, то есть  , в противном случае дробь неправильная.
, в противном случае дробь неправильная.
Определение 3. Дробь называется несократимой, если многочлены в числителе и знаменателе не имеют общих корней.
Интегрирование простейших рациональных дробей
Известны 4 простейшие дроби. Интегралы от них вычисляются следующим образом
I.  . Доказательство:
. Доказательство:  .
.
II.  .
.
Доказательство: 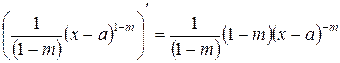 .
.
III.  , IV.
, IV. 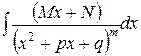
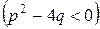 .
.
(при 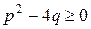 эти два интеграла сводятся к первым двум интегралам).
эти два интеграла сводятся к первым двум интегралам).
Продемонстрируем процедуру вычисления интеграла третьего типа (она же применима к интегралу четвертого типа, но приводит к более сложным интегралам)

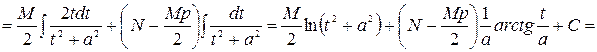
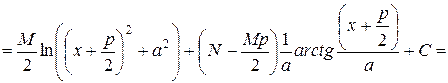
 .
.
Пример.
Вычислить 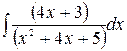 . Поскольку
. Поскольку  , данный интеграл является интегралом третьего типа. Решаем его, используя вышеприведенную процедуру
, данный интеграл является интегралом третьего типа. Решаем его, используя вышеприведенную процедуру
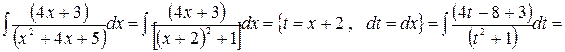
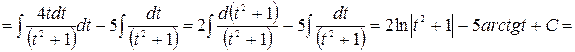
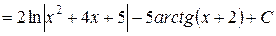 .
.
С интегралом IV типа сложнее. После той же замены переменной получаем
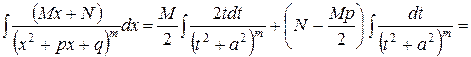
 .
.
Один из интегралов сведен к табличному и вычислен. Для вычисления второго требуется рекуррентная формула
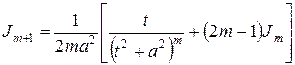 , где
, где 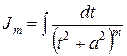 .
.
Пример 1. Вычислить  .
.
Поскольку  , применяем рекуррентную формулу
, применяем рекуррентную формулу
при  :
:
 .
.
Итак,  .
.
Пример 2. Вычислить 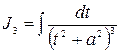 . Применяем рекуррентную формулу при
. Применяем рекуррентную формулу при 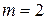 :
:  , но
, но 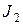 определено выше, тогда
определено выше, тогда
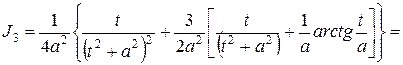
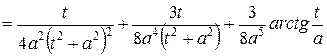 .
.
|
|
|
Тогда
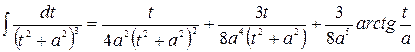 .
.
Пример 3. Вычислить  .
.
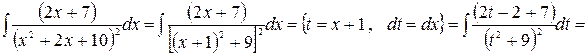
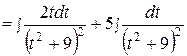 .
.
Поскольку
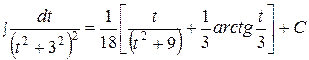 ,
,
что следует из примера 1, получаем
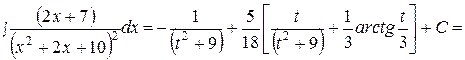
 .
.
Правила интегрирования дробно-рациональных функций
При вычислении  следует руководствоваться правилами.
следует руководствоваться правилами.
1. Установить, является ли подынтегральная функция правильной или неправильной дробью. Если дробь неправильная, представить ее в виде суммы целой части и правильной дроби, с помощью "деления углом", или каким либо другим методом выделив ее целую часть.
2. Выяснить, является ли правильная дробь простейшей, если да, то приступить к ее интегрированию.
3. Если дробь не является простейшей, представить ее в виде суммы простейших дробей и после этого приступить к интегрированию.
Замечание. Точное интегрирование дробно-рациональных функций возможно, если многочлен в знаменателе представим в виде произведения простейших множителей, другими словами, известны все его корни.
Рассмотрим интеграл
 .
.
Дробь неправильная  . Выделяем целую часть, применяя процедуру "деления углом", напоминающую деление чисел
. Выделяем целую часть, применяя процедуру "деления углом", напоминающую деление чисел

В результате
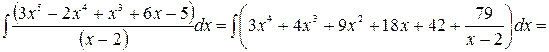
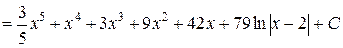 .
.
Примечание. Интегрирование целой части, выделенной из неправильной дроби, трудностей не представляет, поскольку приводит к интегралам от степенных функций. Сложнее с интегрированием правильных дробей, если они не являются простейшими, как в вышеприведенном примере.
Разложение правильной дроби на простейшие
Известно следующее представление правильной дроби в качестве суммы простейших
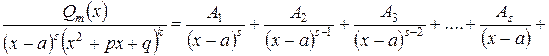
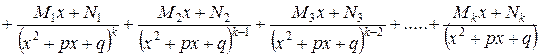 .
.
Для определения коэффициентов этого разложения применяют следующую процедуру
1. Правая часть формулы приводится к общему знаменателю, который должен совпадать со знаменателем дроби в левой части формулы.
2. При этом условии левая и правая дроби равны, если равны их числители, являющиеся многочленами.
3. Поскольку многочлены равны только тогда, когда совпадают коэффициенты при одинаковых степенях переменной, получаем систему уравнений относительно коэффициентов разложения. Известно, что эта система имеет единственное решение.
|
|
|
4. После определения из полученной системы уравнений значений коэффициентов разложения интегрируем простейшие дроби.
Пример 1.
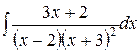 . Имеем интеграл от дробно-рациональной функции, дробь правильная, несократимая и не являющаяся простейшей. Тогда
. Имеем интеграл от дробно-рациональной функции, дробь правильная, несократимая и не являющаяся простейшей. Тогда
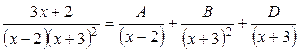 .
.
Отметим, что первый множитель знаменателя дроби дает одну простейшую дробь, так как выражение в скобках в первой степени, второй множитель дает две простейшие дроби, поскольку степень множителя 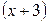 вторая.
вторая.
После приведения правой части равенства к общему знаменателю, совпадающему со знаменателем дроби в левой части равенства, имеем
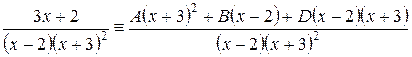 .
.
Эти дроби равны при равенстве их числителей
 ,
,
откуда следует
 . (*)
. (*)
В результате получаем систему трех уравнений с тремя неизвестными
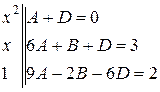
которая может быть решена методами Крамера или Гаусса.
Представляет особый интерес другой подход - добавление к этой системе дополнительных, "лишних" уравнений, упрощающих получение решения. Поскольку (*) есть тождество, оно справедливо при любых значениях переменной 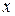 . Следовательно, его можно использовать и при конкретных значениях переменной. Значение
. Следовательно, его можно использовать и при конкретных значениях переменной. Значение 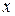 выбирается так, чтобы в уравнение вошло наименьшее число неизвестных.
выбирается так, чтобы в уравнение вошло наименьшее число неизвестных.
Примем  , тогда тождество приводит к уравнению
, тогда тождество приводит к уравнению
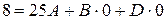 ,
,
в уравнении осталось только A, определяем его  . Из первого уравнения полученной выше системы следует
. Из первого уравнения полученной выше системы следует  , после чего из второго получаем
, после чего из второго получаем  .
.
Поскольку к решению системы привлекалось дополнительное уравнение, третье уравнение системы оказалось лишним. Используем его для проверки полученного результата  .
.
Теперь
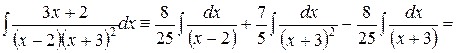
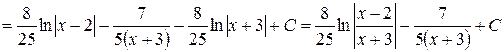 .
.
Пример 2.  .
.
Многочлен в знаменателе необходимо представить в виде произведения простейших множителей. Подбираем один из корней знаменателя, в нашем примере это  . Делим многочлен на
. Делим многочлен на 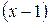
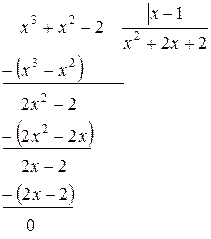
Тогда  , причем второй множитель действительных корней не имеет, поскольку его дискриминант равен
, причем второй множитель действительных корней не имеет, поскольку его дискриминант равен 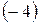 . В результате
. В результате
 .
.
После приведения правой части к общему знаменателю, имеем
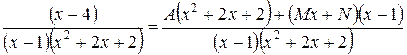 ,
,
откуда следует
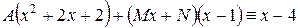 .
.
Это тождество приводит к системе уравнений
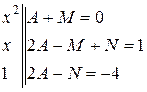
Добавим к этой системе дополнительное уравнение, полученное из тождества при  :
:
|
|
|
 ,
,
откуда следует  . Теперь из первого уравнения системы
. Теперь из первого уравнения системы 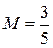 , из последнего уравнения
, из последнего уравнения  . Проверим результат, подставив полученные значения коэффициентов в оставшееся второе уравнение
. Проверим результат, подставив полученные значения коэффициентов в оставшееся второе уравнение
 .
.
В итоге
 .
.
Первый интеграл практически табличный, второй является интегралом третьего типа, решаем его, используя описанную выше процедуру.
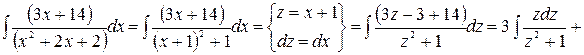
 .
.
Итак,
 .
.
Пример 3. 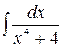 .
.
 .
.
Ни один из полученных квадратных трехчленов не имеет действительных корней. Итак,
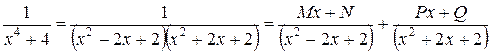 .
.
После приведения дробей к общему знаменателю приходим к тождеству
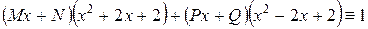
или
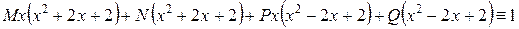 .
.
Приравниваем коэффициенты при одинаковых степенях многочленов в левой и правой частях тождества
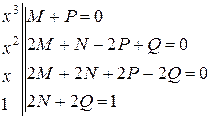
Третье уравнение системы с помощью первого уравнения приводится к виду 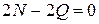 , откуда имеем
, откуда имеем  . Теперь из последнего уравнения получаем
. Теперь из последнего уравнения получаем 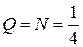 . Из первого уравнения имеем
. Из первого уравнения имеем 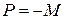 . Подставляя все это во второе уравнение, получаем
. Подставляя все это во второе уравнение, получаем 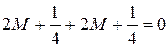 , откуда следует
, откуда следует  , после чего
, после чего 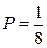 . Итак,
. Итак,
 .
.
Вычисляем интегралы
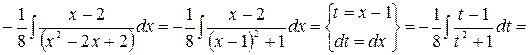

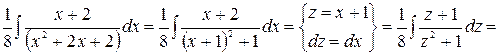
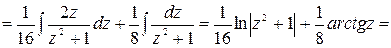
 .
.
В итоге
 .
.
Примечание. Разложение правильной дроби на простейшие можно осуществлять с помощью компьютера.
Примеры для самостоятельного решения
Вычислить интегралы
16.  , 17.
, 17.  , 18.
, 18. 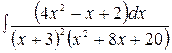 ,
,
19. 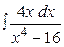 , 20.
, 20. 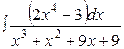 .
.
Тригонометрические и показательные функции
1. Рассматриваются интегралы 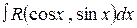 , где
, где  дробно-рациональная функция, двух аргументов
дробно-рациональная функция, двух аргументов 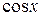 и
и 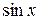 . Другими словами, в числителе и знаменателе этой дроби присутствуют только целые, положительные степени этих аргументов.
. Другими словами, в числителе и знаменателе этой дроби присутствуют только целые, положительные степени этих аргументов.
Заменой переменной эти интегралы сводятся к интегралам 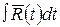 , причем
, причем 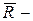 дробно-рациональная функция, но уже аргумента
дробно-рациональная функция, но уже аргумента 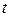 , что приводит поставленную задачу к задаче предыдущего параграфа.
, что приводит поставленную задачу к задаче предыдущего параграфа.
Этот переход может быть осуществлен с помощью, так называемой, универсальной подстановки  , тогда
, тогда 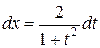 .
.
Нетрудно показать, что
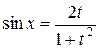 ,
, 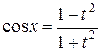 .
.
Итак,
 .
.
Указанная подстановка позволяет свести рассматриваемый интеграл к интегралу от дробно-рациональной функции. Однако, как показывает опыт, эта замена чаще всего приводит к интегралам вычисление которых весьма затруднительно, а иногда невозможно.
В некоторых случаях с помощью других подстановок удается получить более простые дробно-рациональные функции. В отличие от универсальной, эти подстановки, называют иногда специальными, так как применимы они лишь при выполнении некоторых условий.
|
|
|
1. Замена  применима при выполнении условия
применима при выполнении условия
 ,
,
то есть подынтегральная функция нечетна относительно 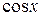 .
.
2. Замена  применима при выполнении условия
применима при выполнении условия
 ,
,
3. Замена 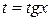 применима при выполнении условия
применима при выполнении условия
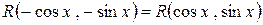 .
.
Это условие реализуется, когда функция 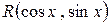 либо четна, либо нечетна одновременно относительно
либо четна, либо нечетна одновременно относительно 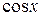 и
и 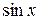 .
.
Таким образом, применение универсальной подстановки целесообразно, когда не работает ни одна из специальных подстановок.
Пример 1. Вычислить 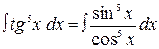 .
.
В этом интеграле допустимы и универсальная, и все специальные подстановки, однако, наиболее удобная из них  :
:
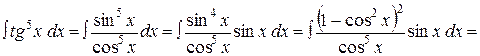
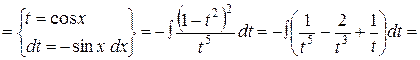
 .
.
Пример 2. Вычислить  . В этом случае не работает ни одна из специальных подстановок, приходится применять универсальную
. В этом случае не работает ни одна из специальных подстановок, приходится применять универсальную
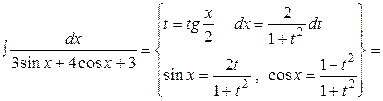
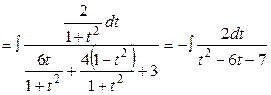 .
.
Знаменатель подынтегральной функции имеет действительные корни, следовательно, она может быть представлена в виде суммы двух простых дробей
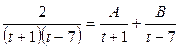 ,
,
откуда следует система уравнений
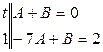 ,
,
решение которой 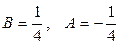 . Итак,
. Итак,
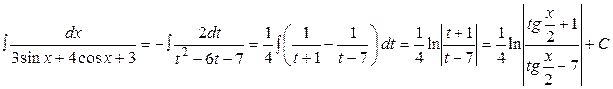 .
.
Интегралы вида 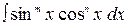 рассмотрим отдельно. Вообще говоря, эти интегралы являются частным случаем интеграла
рассмотрим отдельно. Вообще говоря, эти интегралы являются частным случаем интеграла  , следовательно, к ним применима вышеизложенная теория. Ее следует использовать, когда один из показателей степени нечетен. Если
, следовательно, к ним применима вышеизложенная теория. Ее следует использовать, когда один из показателей степени нечетен. Если 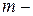 нечетно, то делается замена
нечетно, то делается замена  , если нечетно
, если нечетно  , реализуется замена
, реализуется замена  .
.
Интересен случай, когда 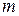 и
и 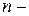 четны. Теория предлагает в этом случае замену
четны. Теория предлагает в этом случае замену 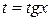 . Однако удобнее использовать одну из формул
. Однако удобнее использовать одну из формул
 .
.
Введение двойного угла позволяет понизить общую степень подынтегральной функции, что, конечно, упрощает вычисление интеграла.
Пример 3.
 .
.
Наконец, интегралы вида  ,
,  ,
, 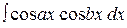 преобразуются с помощью формул
преобразуются с помощью формул
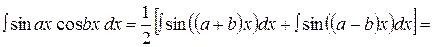
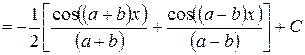 ,
,
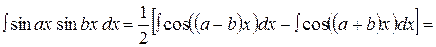
 ,
,
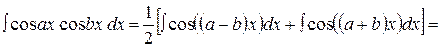
 .
.
Примеры для самостоятельного решения
Вычислить интегралы
21. 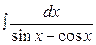 , 22.
, 22. 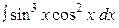 , 23.
, 23. 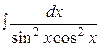 ,
,
24. 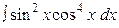 , 25.
, 25. 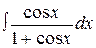 , 26.
, 26.  ,
,
27. 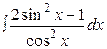 , 28.
, 28.  , 29.
, 29. 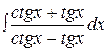 .
.
Показательные функции
Вычисляются интегралы вида 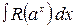 , где
, где  дробно-рациональная функция аргумента
дробно-рациональная функция аргумента 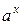 . В этом классе рекомендуется замена
. В этом классе рекомендуется замена 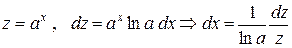 , тогда
, тогда  .
.
Пример.
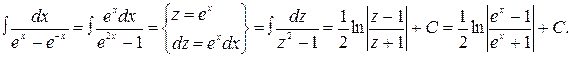
Примеры для самостоятельного решения
30.  , 31.
, 31. 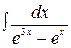 , 32.
, 32.  .
.
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 6881; Нарушение авторских прав?; Мы поможем в написании вашей работы!