
КАТЕГОРИИ:
Архитектура-(3434)Астрономия-(809)Биология-(7483)Биотехнологии-(1457)Военное дело-(14632)Высокие технологии-(1363)География-(913)Геология-(1438)Государство-(451)Демография-(1065)Дом-(47672)Журналистика и СМИ-(912)Изобретательство-(14524)Иностранные языки-(4268)Информатика-(17799)Искусство-(1338)История-(13644)Компьютеры-(11121)Косметика-(55)Кулинария-(373)Культура-(8427)Лингвистика-(374)Литература-(1642)Маркетинг-(23702)Математика-(16968)Машиностроение-(1700)Медицина-(12668)Менеджмент-(24684)Механика-(15423)Науковедение-(506)Образование-(11852)Охрана труда-(3308)Педагогика-(5571)Полиграфия-(1312)Политика-(7869)Право-(5454)Приборостроение-(1369)Программирование-(2801)Производство-(97182)Промышленность-(8706)Психология-(18388)Религия-(3217)Связь-(10668)Сельское хозяйство-(299)Социология-(6455)Спорт-(42831)Строительство-(4793)Торговля-(5050)Транспорт-(2929)Туризм-(1568)Физика-(3942)Философия-(17015)Финансы-(26596)Химия-(22929)Экология-(12095)Экономика-(9961)Электроника-(8441)Электротехника-(4623)Энергетика-(12629)Юриспруденция-(1492)Ядерная техника-(1748)
Делимость целых чисел
|
|
|
|
Наиболее популярными числовыми множествами являются следующие:
N – множество натуральных чисел,
Z – множество целых чисел,
Q – множество рациональных чисел,
R – множество вещественных чисел,
C – множество комплексных чисел.
Они связаны следующим отношением включения: N 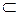 Z
Z 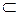 Q
Q 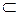 R
R 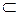 C.
C.
Отношения >, <, ³ и £ полностью упорядочивают множество R. Если A Í R и a Î A, то в дальнейшем будем обозначать A > a, A < a, A ³ a и A £ a подмножества A, состоящие из всех чисел, больших a, меньших a, больших или равных a и меньших или равных a соответственно.
Множество целых чисел Z – счетное, состоит из элементов 0, ±1, ±2,…, ± n,… На нем определены две алгебраические операции – сложение и умножение. Эти операции обладают следующими общими свойствами (для любых a, b, c Î Z):
1. ассоциативность: 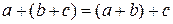 ,
,  ;
;
2. коммутативность: 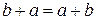 ,
, 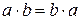 ;
;
3. существуют нейтральные элементы – 0 относительно сложения и 1 относительно умножения соответственно: 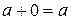 ,
, 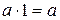 .
.
Кроме того, операция сложения обладает свойством:
4. для каждого 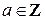 существует единственное
существует единственное 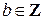 такое, что:
такое, что: 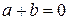 .
.
Ясно, что здесь 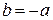 – противоположное целое. Это свойство позволяет ввести на Z вспомогательную операцию – вычитание.
– противоположное целое. Это свойство позволяет ввести на Z вспомогательную операцию – вычитание. 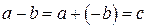 – целое число – разность чисел a и
– целое число – разность чисел a и 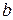 , получаемое вычитанием
, получаемое вычитанием 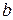 из a.
из a.
Умножение и сложение связаны свойством:
5. 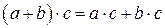 – закон дистрибутивности умножения относительно сложения.
– закон дистрибутивности умножения относительно сложения.
Аналог свойства 4 для умножения выполняется лишь для двух целых чисел: 1 и –1.
Вообще говоря, для каждого целого 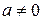 существует обратное относительно умножения (то есть такое число
существует обратное относительно умножения (то есть такое число 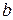 , что
, что 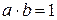 ), но оно является рациональным и не обязательно целым числом. Следовательно, результат операции деления целого числа a на целое число
), но оно является рациональным и не обязательно целым числом. Следовательно, результат операции деления целого числа a на целое число 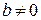 есть число рациональное и в редких случаях является целым. В общем же случае имеет место следующая теорема.
есть число рациональное и в редких случаях является целым. В общем же случае имеет место следующая теорема.
Теорема 1.1.1 (о делении с остатком). Для любых целых чисел a и 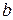 ,
, 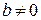 , существуют единственные целые числа
, существуют единственные целые числа 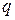 и
и  , 0 £ r < | b |, такие, что
, 0 £ r < | b |, такие, что
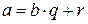 . (1.1.1)
. (1.1.1)
 Доказательство существования.
Доказательство существования.
1. 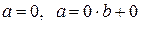 . В этом случае q = r = 0.
. В этом случае q = r = 0.
2. 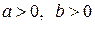 .
.
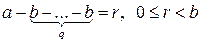 (вычитаем из a b столько раз, чтобы получилось число 0 или число r < b),
(вычитаем из a b столько раз, чтобы получилось число 0 или число r < b), 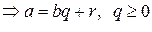 .
.
3. 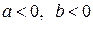 .
.
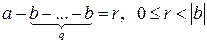 ,
, 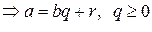 .
.
4. 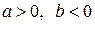 .
.
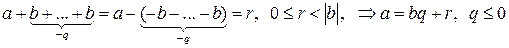 .
.
5. 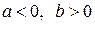 .
.
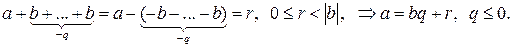
Доказательство единственности.
Пусть a = bq 1 + r 1 и a = bq 2 + r 2. Вычтем из 1-го равенства 2-е:
0 = bq 1 – bq 2 + r 1 – r 2,
b (q 2 – q 1) = r 1 – r 2.
Пусть q 1 ¹ q 2, тогда | r 1 – r 2 | ³ | b |, но 0 £ r 1, r 2 < | b |, Þ | r 1 – r 2 | < | b |. Значит, q 1 = q 2, поэтому и r 1 = r 2.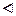
Определение 1.1.1. В равенстве (1.1.1)  называют остатком, а
называют остатком, а 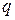 – частным (неполным частным при
– частным (неполным частным при 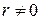 ) от деления a на
) от деления a на 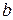 .
.
Для нахождения частного и остатка можно использовать метод деления «уголком».
|
|
|
|
Дата добавления: 2014-01-07; Просмотров: 362; Нарушение авторских прав?; Мы поможем в написании вашей работы!