Понятие о дифференциальном уравнении. Общее и частное решения

Теория дифференциальных уравнений возникла в конце 17 века под влиянием потребностей механики и других естественнонаучных дисциплин, по существу одновременно с интегральным и дифференциальным исчислением.

Определение 1. Обыкновенным дифференциальным уравнением n-го порядка называется уравнение вида 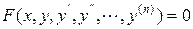, в котором 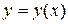- неизвестная функция.

Определение 2. Функция 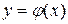называется решениям дифференциального уравнения на промежутке I, если при подстановке этой функции и ее производных дифференциальное уравнение обращается в тождество.

Решить дифференциальное уравнение - это найти все его решения.

Определение 3. График решения дифференциального уравнения называется интегральной кривой дифференциального уравнения.

Определение 4. Обыкновенным дифференциальным уравнением 1 -го порядка называется уравнение вида .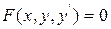

Определение 5. Уравнение вида 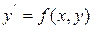называется дифференциальным уравнением 1 -го порядка, разрешенным относительно производной.

Как правило, любое дифференциальное уравнение имеет бесконечно много решений. Чтобы выделить из совокупности всех решений какое-либо одно, надо наложить дополнительные условия.

Определение 6. Условие вида 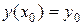, накладываемое на решение дифференциального уравнения 1-го порядка, называется начальным условием, или условием Коши.

Геометрически это означает, что соответствующая интегральная кривая проходит через точку .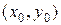

Определение 7. Общим решением дифференциального уравнения 1-го порядка 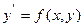на плоской области D называется однопараметрическое семейство функций 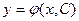, удовлетворяющее условиям:

1) для любого 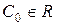функция 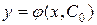является решением уравнения;

2) для каждой точки существует такое значение параметра 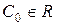, что соответствующая функция 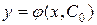является решением уравнения, удовлетворяющим начальному условию .

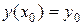Определение 8. Решение, получаемое из общего решения при некотором значении параметра, называется частным решением дифференциального уравнения.

Определение 9. Особым решением дифференциального уравнения называется всякое решение, которое не может быть получено из общего решения ни при каком значении параметра.

Решение дифференциальных уравнений - очень сложная задача, и, вообще говоря, чем выше порядок уравнения, тем труднее указать способы решения уравнения. Даже для дифференциальных уравнений первого порядка удается лишь в небольшом числе частных случаев указать приемы нахождения общего решения. Более того, и в этих случаях искомое решение не всегда является элементарной функцией.

Одна из основных задач теории дифференциальных уравнений, впервые изучавшаяся О. Коши, состоит в отыскании решения дифференциального уравнения, удовлетворяющего заданным начальным условиям.

Например, всегда ли существует решение дифференциального уравнения 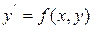, удовлетворяющее начальному условию 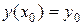, и будет ли оно единственным? Вообще говоря, ответ отрицательный. В самом деле, уравнение 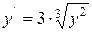, правая часть которого непрерывна на всей плоскости, имеет решения y =0 и y =(x + C)³, C Î R. Следовательно, через любую точку оси О х проходит две интегральные кривые.

Таким образом, функция должна удовлетворять некоторым требованиям. В следующей теореме содержится один из вариантов достаточных условий для существования и единственности решения дифференциального уравнения 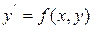, удовлетворяющего начальному условию .

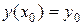Теорема 1. Пусть функция 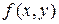и ее частная производная 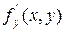непрерывны в некоторой области D на плоскости х О у, точка .

Тогда в некотором интервале, содержащем х₀, существует, и притом единственное, решение 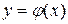дифференциального уравнения 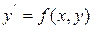, удовлетворяющее начальному условию .

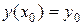Дата добавления: 2014-01-07