Признаки существования предела (с доказательством теоремы о пределе промежуточной функции)

Определение 1. Последовательностью называется функция, заданная на множестве натуральных чисел, т.е. a_n = f (n) при n Î N.

Обозначения: { a_n: n Î N } или (a_n).

Пример 1. a_n =1/ n. a ₁=1, a ₂=1/2, a ₃=1/3, a ₄=1/4, …, a ₁₀=1/10,…, a ₁₀₀=1/100,….

Можно показать, что эта последовательность является убывающей, ограниченной снизу (например, числом 0), и её элементы приближаются к числу 0 при неограниченном возрастании n.

Пример 2. a_n =(2 n +1)/(3 n +5). a ₁=3/8, a ₂=5/11, a ₃=7/14, a ₄=9/17, …, a ₁₀=21/35,…, a ₁₀₀=201/305,….

Можно показать, что эта последовательность является возрастающей, ограниченной сверху (например, числом 1), и её элементы приближаются к числу 2/3 при стремлении n к бесконечности.

Понятие предела последовательности является характеристикой поведения элементов последовательности при возрастании их номеров.

Определение 2. Число A называется пределом последовательности (a_n), если элементы этой последовательности a_n приближаются (стремятся) к числу A при возрастании их номеров n.

Обозначения: a_n ® A при n ®¥ или .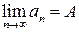

Например, , 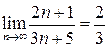. Более строго:

Определение 2¢. Число A называется пределом последовательности (a_n), если для любого положительного как угодно малого числа e>0 существует номер N (зависящий от e) такой, что для всех членов последовательности с номерами n > N выполняется неравенство ½ a_n - A ½<e.

Заметим, что неравенство ½ a_n - A ½<e равносильно двойному неравенству A -e< a_n < A +e.

Определение 3. Последовательность (a_n) называется возрастающей, если для любого n Î N выполняется неравенство a_n < a_{n+ 1}.

Определение 4. Последовательность (a_n) называется убывающей, если для любого n Î N выполняется неравенство a_n > a_{n+ 1}.

Возрастающие и убывающие последовательности называются монотонными.

Определение 5. Последовательность (a_n) называется ограниченной, если существует число M >0 такое, что для любого n Î N выполняется неравенство ½ a_n ½<M.

Теорема 1. Всякая монотонная ограниченная последовательность имеет предел.

Теорема 2. Пусть 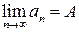, и последовательность (c_n) такова, что, начиная с некоторого номера, выполняется неравенство a_n £ c_n £ b_n. Тогда .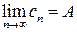

Замечание 1. При решении задачи на вычисление предела последовательности будем использовать не определение, а теоремы о пределах и известные пределы:

, , , .

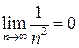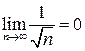Задача 1. Вычислить предел последовательности:

Задача 2. Вычислить предел последовательности: .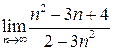

Решение. Имеет место неопределенность вида 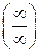. Теоремы о пределах применить нельзя. Проведем тождественные преобразования, цель которых — получение последовательности, к которой можно применить теоремы о пределах.

Числитель и знаменатель дроби поделим на старшую степень n ². Получим .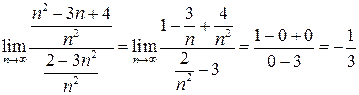

Определение 6. Число A называется пределом функции y = f (x) при x ®+¥, если значения функции f (x) приближаются (стремятся) к числу A при неограниченном возрастании аргумента x.

Обозначения: f (x)® A при x ® +¥ или 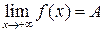. Более строго:

Определение 6¢. Число A называется пределом функции y = f (x) при x ®+¥, если для любого положительного как угодно малого числа e>0 существует положительное число M >0 (зависящее от e) такое, что для всех значений аргумента x ÎD(f), удовлетворяющих условию x > M, выполняется неравенство ½ f (x)- A ½<e.

Определение 7. Число A называется пределом функции y = f (x) при x ®-¥, если значения функции f (x) приближаются (стремятся) к числу A, когда аргумент x, оставаясь отрицательным, неограниченно возрастает по абсолютной величине.

Обозначения: f (x)® A при x ® -¥ или .

Определение 8. Число A называется пределом функции y = f (x) при x ®¥, если значения функции f (x) приближаются (стремятся) к числу A при неограниченном возрастании аргумента x по абсолютной величине.

Обозначения: f (x)® A при x ®¥ или .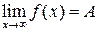

Пример 3. Вычислить предел функции .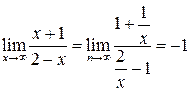

Пример 4. Выяснить, существует ли предел функции .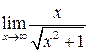

Решение. Имеет место неопределенность вида 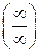. Теоремы о пределах применить нельзя. Рассмотрим два случая.

Пусть x >0. Тогда 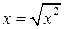. Следовательно: .

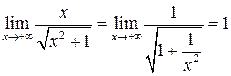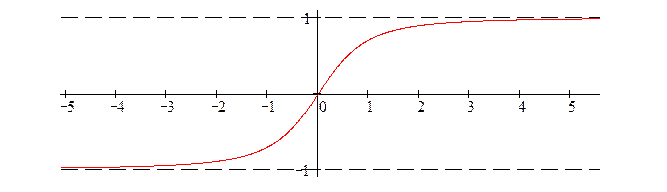Если же x <0, то 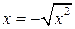. Следовательно: .

Итак, функция 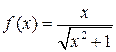не имеет предела при x ® ¥.

Дата добавления: 2014-01-07