Нормальный закон распределения

Нормальный закон распределения

ЛЕКЦИЯ 6

Тема 5: Непрерывные случайные величины.

ПЛАН

1. Определение нормального закона распределения.

2. Формулы для определения вероятностей: а) попадания нормально распределенной случайной величины в заданный интервал; б) ее отклонения от математического ожидания. Правило трех сигм.

3. Центральная предельная теорема. Понятие о теореме Ляпунова.

Для непрерывных случайных величин особо важное значение имеет нормальный закон распределения. Необходимо знать теоретико-вероятностный смысл его параметров, выражение функции распределения F_N (x) через функцию Лапласа Ф (х), свойства нормально распределенной случайной величины, правило трех сигм, важно четко представлять, что нормальный закон, в отличие от других, является предельным законом, к которому при некоторых весьма часто встречающихся условиях приводит совокупное действие (сумма) п независимых случайных величин Х ₁, Х ₂, …, Х_n при п ®¥.

Определение 1. Непрерывная случайная величина Х имеет нормальный закон распределения (закон Гаусса) с параметрами a и s ², если ее плотность вероятности имеет вид:

.

Многие величины подчиняются нормальному закону, например, рост человека, дальность полета снаряда и т.п.

Кривую нормального закона распределения называют нормальной кривой или гауссовой кривой.

Теорема 1. Математическое ожидание случайной величины Х, распределенной по нормальному закону, равно параметру а этого закона, т.е. M (X)= a, а ее дисперсия равна параметру s ², т.е. D (X)= s ².

Доказательство. Математическое ожидание случайной величины Х:

.

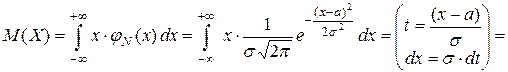
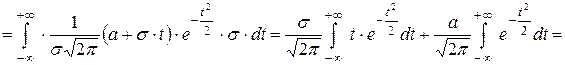
Первый интеграл равен нулю как интеграл от нечетной функции по симметричному промежутку. Второй интеграл – это интеграл Пуассона, равный .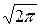

Дисперсия случайной величины Х:

.

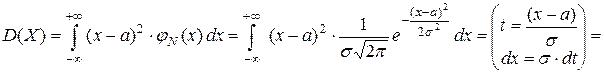
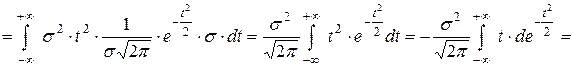
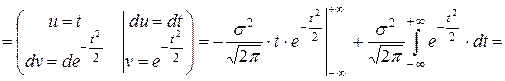
При изменении параметра a гауссова кривая параллельно смещается вдоль оси О х.

При изменении параметра s ² изменяется ордината максимума гауссовой кривой.

Нормальный закон распределения случайной величины с параметрами a =0 и s ²=1 называется стандартным (или нормированным), а соответствующая нормальная кривая – стандартной.

Функция распределения НСВ выражается через плотность вероятности по формуле .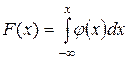

Следовательно, функция распределения нормально распределенной случайной величины выражается по формуле 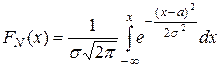, в которой подынтегральная функция не имеет первообразной функции, выражающейся через элементарные функции.

Поэтому ее выражают через функцию Лапласа , для которой составлены таблицы.

Теорема 1. Функция распределения случайной величины, распределенной по нормальному закону, выражается через функцию Лапласа F (x) по формуле:

.

Дата добавления: 2014-01-07