Потоки событий. Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени

Потоком событий называется последовательность событий, происходящих одно за другим в какие-то случайные моменты времени.

Различают потоки однородных и неоднородных событий. В однородном потоке события отличаются только моментами времени.

Поток событий графически можно представить как последовательность точек t ₁, t ₂, … t_i на числовой оси 0 t, соответствующих моментов появления событий (рис. 2.1).

Рис. 2.1

Потоки событий различаются по своей внутренней структуре. Самым простым потоком с позиции его построения является регулярный поток.

Регулярным потоком называется поток, в котором события следуют одно за другим через строго определенные промежутки времени. Строго регулярных потоков в природе не существует, так как моменты появления событий всегда содержат элементы случайностей. Однако даже как идеализированная схема, регулярный поток не имеет преимуществ, так как уступает по простоте расчетов другим типам потоков.

Рассмотрим поток, в котором события разделены интервалами времени T ₁, T ₂, …. Эти интервалы вообще являются случайными величинами (рис. 2.2).

Рис. 2.2

Пусть T ₁, T ₂, …. независимы между собой. В этом случае поток событий называется потоком с ограниченным последействием или потоком Пальма.

Поток событий называется ординарным, если вероятность того, что на малый участок D t, примыкающий к моменту времени t попадает больше одного события (рис. 2.3).

Рис. 2.3

T.е. [ P> 1 (t, Dt)] пренебрежимо мала по сравнению с вероятностью того, что на этом же интервале времени попадает ровно одно событие (P ₁(t, D t)):

P ₁(t, D t) >> P _>1(t, D t). (2.39)

Так как для любого интервала D t

P ₀(t, D t) + P ₁(t, D t) + P _>1(t, D t) =1, (2.40)

как сумма вероятностей событий, образующих полную группу событий и несовместимых, то для ординарного потока событий

P ₀(t, D t) + P ₁(t, D t)»1;

P _>1(t, D t) = Q (D t), (2.41)

где Q (D t) – величина, порядок малости которой выше, чем D t

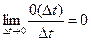. (2.42)

Примерами ординарного потока поток отказов в вычислительной системы.

Неординарные потоки на практике встречаются значительно реже, чем ординарные потоки событий (поток пассажиров, прибывающих на данный этаж). Мы будем рассматривать только ординарные потоки событий.

Стационарным потоком событий является поток, для которого вероятность появления того или другого числа событий на участке времени tзависит лишь от длины участка и не зависит от того, где на оси времени взят этот участок.

Очевидно регулярный поток с одинаковыми интервалами между событиями, а также поток пальма с одинаковыми распределениями времени Т ₁, Т ₂ представляют собой стационарные потоки.

Рассмотрим на оси 0 t ординарный поток событий и найдем среднее число событий, наступающих на интервале D t примыкающих к моменту времени t. В соответствии с приближенным неравенством оно будет

0 ×P ₀(t, D t) +1× P ₁(t, D t) = P ₁(t, D t) (2.43)

Среднее число событий поступающих на участке времени D t в единицу времени составит:

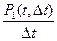. (2.44)

Рассмотрим предел выражения при D t ®0. Если этот предел существует, то он называется интенсивностью (плотностью, параметром) ординарного потока.

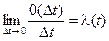. (2.45)

Интенсивность потока может быть любой неотрицательной функцией времени. Она имеет размерность обратную размерности времени (1/ t). Для стационарного потока его интенсивность не зависит от времени и представляет собой постоянную величину, равную среднему числу событий, наступающих в единицу времени:

l(t)=l=const. (2.46)

Дата добавления: 2014-01-07